Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Явление самоиндукции. Индуктивность

Явление электромагнитной индукции наблюдается во всех случаях, когда изменяется магнитный поток, пронизывающий контур. При этом совершенно не важно, чем вызывается это изменение потока. Если в некотором контуре течет изменяющийся во времени ток, то магнитное поле этого тока также будет изменяться. Это приводит к изменению магнитного потока через контур, а, следовательно, к появлению ЭДС индукции в контуре. Таким образом, изменение тока в контуре ведет к возникновению ЭДС индукции в этом же самом контуре. Это явление, открытое Д. Генри в 1837 г., называют самоиндукцией, а дополнительные токи, вызываемые ЭДС самоиндукции, - экстратоками самоиндукции.

Так как в соответствии с законом Био-Савара-Лапласа величина магнитной индукции пропорциональна силе тока I, то и магнитный поток Ф, пронизывающий контур, пропорционален силе тока:

Ф = LI, (30.1)

где коэффициент пропорциональности L называют индуктивностью контура или коэффициентом самоиндукции.

В соответствии с принятым правилом знаков для величин Ф и I оказывается, что Ф и I всегда имеют одинаковые знаки. Это означает, что индуктивность L – величина всегда положительная.

Из выражения (30.1) определяется единица индуктивности генри (Гн): 1 Гн - индуктивность такого контура, магнитный поток сквозь который при силе тока 1 А равен 1 Вб: 1 Гн=1 Вб/А.

Индуктивность L зависит от формы и размеров контура, а также от магнитных свойств окружающей среды. Если контур жесткий (недеформируемый) и поблизости от него нет ферромагнетиков, индуктивность L = const и не зависит от силы тока I. Для длинного соленоида, когда его длину можно считать большой по сравнению с его диаметром, индуктивность выражается формулой:

L = m₀ S = m₀n²V, (30.2)

где m₀ – магнитная постоянная, N – полное число витков, l – длина соленоида, S – площадь сечения соленоида, n=N/l – число витков на единицу длины, V = Sl – объем соленоида.

При изменении силы тока в контуре согласно (27.2) возникает ЭДС самоиндукции E_i:

E_i = - 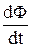= - 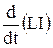. (30.3)

Если при изменении силы тока индуктивность L остается постоянной (не меняется конфигурация контура, отсутствуют ферромагнитные сердечники), то

E_i = - . (30.4)

Знак минус показывает, что в соответствии с правилом Ленца электродвижущая сила самоиндукции направлена таким образом, чтобы препятствовать изменению силы тока. Из (30.4) опять можно определить единицу измерения индуктивности L: 1 Гн – индуктивность такого контура, в котором изменение тока на 1 А за 1 с возбуждает в нем ЭДС самоиндукции 1 В.

В замкнутой цепи, содержащей источник тока с ЭДС Е, катушку индуктивности и резистор с сопротивлением R, закон Ома имеет вид:

IR = E_i - . (30.5)

Из (30.5) следует, что установление тока при замыкании цепи и убывание тока при размыкании цепи происходят не мгновенно, а постепенно. Этот эффект тем заметней, чем больше индуктивность L, и он связан с тем, что дополнительные токи, возникающие вследствие самоиндукции, всегда направлены так, чтобы противодействовать изменениям тока в цепи. Причем в цепях, содержащих катушки с большой индуктивностью (электромагниты, электродвигатели, электрогенераторы, трансформаторы), и в которых после размыкания цепи остаются замкнутые контуры, возникают экстратоки размыкания значительной силы. Это может привести к образованию электрической дуги между контактами выключателя. Для предотвращения разрушительного действия больших экстратоков в подобных цепях ставят реостаты, с помощью которых перед выключением рубильников значительно увеличивают сопротивления контуров.

Индуктивность любого контура зависит от свойств среды, в которой он находится. Если обозначить L₀ – индуктивность контура в вакууме, а L - индуктивность того же контура в однородном веществе, то отношение

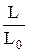= m (30.6)

называют магнитной проницаемостью вещества. Магнитная проницаемость m характеризует магнитные свойства вещества и зависит от рода вещества. Отсюда следует, что индуктивность соленоида с сердечником из вещества с магнитной проницаемостью m будет равна (см. (30.2)):

L = mL₀ = mm₀ S = mm₀n²V. (30.7)

Поскольку индуктивность контура пропорциональна магнитной проницаемости m окружающей среды, то и магнитный поток, пронизывающий контур, также будет пропорционален m. Следовательно, и магнитная индукция В в среде с магнитной проницаемостью m будет в m раз больше, чем в вакууме В₀, т.е.

В = mВ₀. (30.8)

Тогда выражения для магнитных индукций прямого тока (сравните с (22.4)) и в центре кругового тока (сравните с (22.5)) в среде с магнитной проницаемостью m принимают вид:

В = m 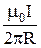; В = m . (30.9)

Из выражения 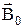= m₀ 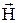(22.6), связывающего 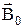и 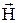в вакууме, и (30.8) получаем для однородной изотропной среды соотношение, связывающее вектор магнитной индукции с напряженностью магнитного поля (см. (34.9)):

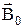= mm₀ 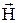. (30.10)

Используя соотношения (30.1) и (30.7), с учетом того, что полный магнитный поток через соленоид равен Ф = NBS, приходим к выражению для магнитной индукции внутри соленоида:

B = mm ₀ 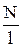I = mm₀nI. (30.11)