Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Магнитное поле движущегося заряда

Каждый проводник с током создает в окружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле. Из формулы (22.2) легко получить выражение для магнитной индукции поля, создаваемого точечным зарядом q, движущимся со скоростью 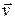. Допустим, что ток создается носителями с зарядом е¢ (знак безразличен), скорость упорядоченного движения которых равна 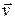. Тогда

I = jS = n e¢ v S, (23.1)

где S – площадь поперечного сечения проводника, n – концентрация носителей тока (число носителей тока в единице объема).

Подставим выражение (23.1) в формулу (22.2):

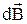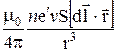= . (23.2)

Учитывая, что векторы е¢ 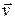и 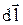совпадают по направлению, заменим е¢ v 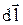на е¢ 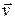dl. Тогда формула (23.2) примет вид

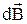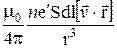= , (23.3)

так как скалярные множители можно вносить и выносить за знак векторного произведения от любого множителя векторного произведения (свойство векторного произведения).

Произведение Sdl соответствует объему отрезка провода длины dl, а n Sdl равно числу носителей тока, содержащихся в этом объеме. Следовательно, разделив выражение (23.3) на n Sdl, найдем магнитную индукцию поля, создаваемого зарядом е¢, движущимся со скоростью 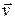в вакууме (в воздухе). Заменив е¢ на q, получим

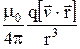= , (23.4)

где 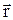- радиус-вектор, проведенный от заряда q к точке поля, r - его модуль, a - угол между векторам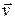и и 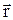(рисунок 32).

Согласно выражению (23.4), вектор направлен перпендикулярно плоскости, в которой расположены векторы 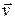и 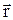, а его направление совпадает с направлением поступательного движения правого винта при его вращении от 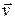к 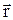. Модуль магнитной индукции (23.4) вычисляется по формуле:

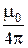
В = . (23.5)

Приведенные соотношения (23.4) и (23.5) справедливы лишь при малых скоростях v (v < < с, с – скорость света в вакууме) движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени находится движущийся заряд.

Формула (23.4) определяет магнитную индукцию положительного заряда, движущегося со скоростью 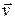. Если движется отрицательный заряд, то q надо заменить на - q. Скорость 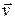- относительная скорость, т. е. скорость относительно наблюдателя. Вектор в рассматриваемой системе отсчета зависит как от времени, так и от положения точки наблюдения. Поэтому следует подчеркнуть относительный характер магнитного поля движущегося заряда.

Впервые поле движущегося заряда удалось обнаружить американскому физику Г. Роуланду (1848-1901). Окончательно этот факт был установлен профессором Московского университета А. А. Эйхенвальдом (1863-1944), изучившим магнитное поле конвекционного тока, а также магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле свободно движущихся зарядов было измерено академиком А. Ф. Иоффе, доказавшим, что электронный пучок и ток проводимости эквивалентны с точки зрения образования магнитного поля.