Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Электрический диполь

Электрический диполь - система двух одинаковых по модулю разноименных точечных зарядов + q и - q, находящихся на некотором расстоянии l друг от друга. Когда говорят о поле диполя, то полагают, что расстояние R от диполя до интересующих нас точек поля значительно больше l (R > > l) и поэтому считают диполь точечным.

С электрическими диполями нам приходится встречаться весьма часто. Небольшое проводящее тело в электрическом поле можно приближенно рассматривать как диполь, так как на его концах возникают индукционные заряды, равные по величине и разноименные по знаку. Подобные же заряды возникают и на диэлектриках, и поэтому небольшое диэлектрическое тело в электрическом поле также можно рассматривать как диполь. Наконец, многие молекулы построены из положительных и отрицательных ионов, центры которых смещены друг относительно друга. Такие молекулы можно считать во многих случаях электрическими диполями.

Найдем силы, действующие на диполь в однородном электрическом поле (рисунок 8). На концы диполя действуют равные по величине силы F = q E, где Е - напряженность поля. Эти силы направлены в противоположные стороны и образуют пару сил. Момент М этой пары равен:

M=F× l × sina= q E× l × sina, (5.1)

где a - угол между вектором 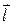и напряженностью .

Мы видим, что величина момента пары сил зависит от произведения заряда q на длину диполя l. Это произведение называют моментом диполя. Момент диполя есть вектор, равный

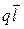= . (5.2)

Электрический момент диполя направлен так же, как и плечо диполя 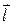, т.е. от отрицательного заряда к положительному. Единица измерения момента электрического диполя есть кулон× метр (Кл× м).

Пользуясь понятием момента диполя, можно написать выражение для момента пары сил, действующей на диполь, в виде

М = р Е× sina. (5.3)

Направление момента этой пары 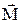совпадает с направлением оси вращения диполя, т.е. перпендикулярно к и , и выражается векторным уравнением:

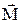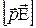= . (5.4)

Момент сил (5.4) стремится повернуть диполь так, чтобы его электрический момент установился по направлению поля.

В случае нахождения диполя в неоднородном электрическом поле силы, действующие на концы диполя, уже неодинаковы, и поэтому их результирующая сила не равна нулю. В неоднородном электрическом поле на диполь действует результирующая сила, стремящаяся передвинуть диполь в область поля с большей напряженностью.

Прямая, проходящая через заряды диполя, называется осью диполя. Вычислим сначала потенциал, а затем напряженность поля диполя. Это поле обладает осевой симметрией. Поэтому картина поля в любой плоскости, проходящей через ось диполя, будет одной и той же, причем вектор лежит в этой плоскости.

Согласно (4.9) потенциал поля диполя в точке А (рисунок 9а) определяется как

j= . (5.5)

Так как R₁ и R₂ много больше l, то можно считать R₁R₂=R², где R - расстояние от точки А до диполя (диполь точечный!). Из рисунка 9а видно, что R₁-R₂= l cosJ. С учетом этого выражение (5.5) примет вид

j= , (5.6)

где p = ql - электрический момент диполя.

Из формулы (5.6) видно, что поле диполя зависит от его электрического момента . Как мы отметили в уравнении (5.4) поведение диполя во внешнем поле также зависит от . Следовательно, является важной характеристикой диполя. Следует также обратить внимание на то, что потенциал поля диполя убывает с расстоянием R быстрее, чем потенциал поля точечного заряда (1/R² вместо 1/R).

Чтобы найти напряженность электрического поля диполя, вычислим по формуле (4.17) проекции вектора на два взаимно перпендикулярных направления. Одно из них определяется движением точки, вызванном изменением расстояния R (при фиксированном J), второе – движением точки, обусловленном изменением угла J (при фиксированном R; см. рисунок 9а). Первая проекция получается путем дифференцирования выражения (5.6) по R:

E_R= 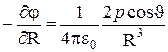. (5.7)

Вторая проекция равна

Е_J= . (5.8)

Как видно из рисунка 9а модуль вектора равен:

Е= = . (5.9)

Как следует из выражения (5.9), напряженность поля диполя убывает с расстоянием от диполя как 1/R³, т.е. быстрее, чем напряженность поля точечного заряда (убывающая как 1/R²). Ориентацию вектора напряженности поля диполя в произвольной точке А пространства (см. рисунки 9а и 9б) характеризует угол b между радиус-вектором 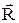от диполя к выбранной точке и напряженностью . Поделив почленно соотношения (5.8) и (5.7) друг на друга имеем:

tgb = 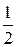tgJ. (5.10)

Диполь с электрическим моментом во внешнем электрическом поле с напряженностью обладает потенциальной энергией (см. рисунок 8):

W= - = - р Е× cosa. (5.11)

Нужно отметить, что это выражение не учитывает энергию взаимодействия зарядов + q и - q, образующих диполь.