Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Закон Кулона

Закон взаимодействия неподвижных точечных электрических зарядов установлен в 1785 г. Ш. Кулоном (примерно за 11 лет до Кулона этот закон был получен Г. Кавендишем, однако его работа оставалась неизвестной в течение более 100 лет). К этому времени большинство ученых уже предполагали, что по аналогии с законом Всемирного тяготения сила взаимодействия зарядов должна быть обратно пропорциональна квадрату расстояния между ними. Точность измерений Кулона была невысокой, но достаточной для того, чтобы показать правдоподобность закона обратных квадратов.

Для заряженных тел произвольных размеров такой закон в общей форме дать нельзя, так как сила взаимодействия протяженных тел зависит от их формы и взаимного расположения. Однако форма тел и их взаимная ориентация перестают сказываться, если размеры тел весьма малы по сравнению с расстоянием между ними. Под точечным зарядом в физике понимают протяженное заряженное тело, размеры которого пренебрежимо малы по сравнению с расстоянием до других зарядов. Понятие точечного заряда, как и материальной точки, является физической абстракцией.

С помощью крутильных весов Кулон измерял силу взаимодействия двух заряженных шариков в зависимости от величины зарядов на них и от расстояния между ними. При этом Кулону в своих опытах не было необходимости знать абсолютную величину зарядов на шариках. Он исходил из того, что при касании к заряженному шарику точно такого же незаряженного шарика заряд распределяется между обоими шариками поровну. Таким образом, Кулон получал равные заряды или известные доли первоначальных зарядов на двух различных шарах.

Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна величинам зарядов q ₁ и q ₂ и обратно пропорциональна квадрату расстояния R между ними:

F=k 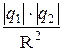, (2.1)

где k - коэффициент пропорциональности, зависящий от выбора системы единиц, и 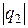- модули зарядов.

Сила (называемая кулоновской) направлена по прямой, соединяющей взаимодействующие заряды. Она соответствует притяжению в случае разноименных зарядов и отталкиванию в случае одноименных зарядов. Опытная проверка закона Кулона проводится в воздухе, так как влияние воздуха на силы взаимодействия очень мало и в большинстве случаев им можно пренебречь.

В векторной форме закон Кулона записывается:

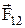=k 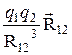, (2.2)

где 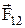- сила, действующая на заряд q ₁ со стороны заряда q ₂, 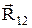- радиус-вектор, проведенный от заряда q ₂ к заряду q ₁, R= .

На заряд q ₂ со стороны заряда q ₁ действует сила = - 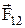, т. е. взаимодействие электрических точечных зарядов удовлетворяет третьему закону Ньютона.

В СИ коэффициент пропорциональности равен k=1/4pe₀, т.е.

F= 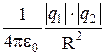, (2.3)

Величина e₀ называется электрической постоянной; она относится к числу фундаментальных физических постоянных и равна e₀ = 8, 85× 10^-12Кл²/(Н× м²), или

e₀ = 8, 85× 10^-12 Ф/м, (2.4)

где фарада (Ф) - единица электрической емкости.

Тогда

k=1/4pe₀=9× 10⁹ м/Ф. (2.5)

Опыт показывает, что сила взаимодействия двух данных зарядов не изменяется, если вблизи них поместить еще какие-либо заряды (принцип независимости действия сил). Если в окрестности заряда q помещены еще N зарядов q ₁, q ₂,..., q _N, то результирующая сила , с которой действуют на q все N зарядов q _i, определяется формулой:

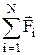= , (2.6)

где 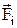- сила, с которой действует на q заряд q _i в отсутствие остальных N-1 зарядов.

Из формулы (2.6), выражающей принцип суперпозиции для силы, следует, что, зная закон взаимодействия между точечными зарядами, можно вычислить силу взаимодействия между зарядами, сосредоточенными на телах конечных размеров. Для этого нужно мысленно разбить каждое тело на столь малые кусочки с зарядом dq, чтобы их можно было считать точечными, вычислить по формуле (2.2) силу взаимодействия между зарядами dq, взятыми попарно, и затем произвести векторное сложение этих сил.

Иногда, когда заряженное тело конечных размеров нельзя принять за точечный заряд, необходимо знать распределение зарядов внутри тела. При этом для упрощения математических расчетов во многих случаях бывает удобно игнорировать тот факт, что заряды имеют дискретную структуру (электроны, ядра), и считать, что они «размазаны» определенным образом в пространстве. Другими словами, удобно заменить истинное распределение точечных дискретных зарядов фиктивным непрерывным распределением. Это позволяет значительно упрощать расчеты, не внося сколько-нибудь значительной ошибки. При переходе к непрерывному распределению вводят понятие плотности зарядов – объемной r, поверхностной s и линейной t. По определению,

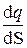r= , s= , t= 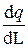, (2.7)

где d q – заряд, заключенный соответственно в объеме dV, на поверхности dS и на длине dL.

Опыты Кулона являются не единственным доказательством справедливости закона обратных квадратов. В настоящее время имеется большое количество других экспериментальных данных, показывающих, что закон Кулона выполняется очень точно как для очень больших, так и для очень малых расстояний. В частности, исследования атомных явлений позволяет заключить, что он справедлив, по крайней мере, вплоть до расстояний порядка 10^-15 м.