💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Потенциал. Связь между потенциалом и напряженностью электрического поля

Для понимания свойств электрического поля большое значение имеет понятие разности потенциалов или электрического напряжения. К этому понятию мы приходим, рассматривая работу сил электрического поля.

Рассмотрим электрическое поле, создаваемое неподвижным точечным зарядом q ₁. Предположим, что электрический заряд q ₂ перемещается из некоторой точки 1 в другую точку 2 (см. рисунок 5). Так как на заряд q ₂ в электрическом поле действует кулоновская сила, то при таком перемещении совершается работа А₁₂. Предположим для определенности, что оба заряда положительные. Тогда на заряд q ₂ со стороны q ₁ действует кулоновская сила отталкивания. 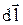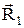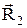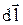Обозначим через – элементарное перемещение заряда q ₂ на произвольном участке траектории, и - радиус-векторы, проведенные от заряда q ₁ к начальной 1 и конечной 2 точкам траектории перемещения q ₂, a - угол между кулоновской силой и перемещением в произвольной точке траектории с радиус-вектором 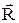, dl× cosa=dR – приращение модуля радиус-вектора.

Запишем выражение для элементарной работы перемещения заряда q ₂ с учетом, что кулоновская сила взаимодействия зарядов определяется соотношением (2.3):

dA= × 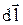=F× dl× cosa=F× dR= 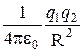× dR. (4.1)

Работа, совершаемая силами поля над зарядом q ₂ при перемещении из точки 1 в точку 2 равна:

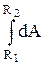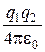
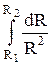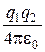
А₁₂= = = 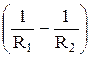. (4.2)

Как видно из (4.2), работа А₁₂ не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.

Из (4.2) следует, что работа перемещения заряда в электростатическом поле по любой замкнутой траектории равна нулю (в этом случае начальная и конечные точки совпадают и R₁=R₂):

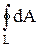=0. (4.3)

Согласно (3.4) на заряд q ₂ в электрическом поле напряженностью действует сила = q ₂ . Тогда в соответствии с (4.1) элементарная работа равна:

dA= × 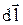= q ₂× × 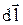= q ₂× Е× dl× cosa= q ₂× Е_l× dl, (4.4)

где Е_l – проекция вектора напряженности на направление перемещения.

Так как в (4.4) множитель q ₂ ¹ 0, выражение (4.3) примет вид:

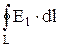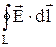= =0. (4.5)

Интеграл (4.5) называют циркуляцией вектора по замкнутому контуру L. Из (4.5) следует, что циркуляция вектора электростатического поля вдоль любого замкнутого контура равна нулю (это условие выражает суть теоремы о циркуляции вектора ). Из обращения в нуль циркуляции вектора следует, что силовые линии не могут быть замкнутыми, они начинаются и заканчиваются на зарядах или уходят в бесконечность.

Тело, находящееся в потенциальном силовом поле (а электростатическое поле является потенциальным), обладает потенциальной энергией, за счет которой силами поля совершается работа. Как известно, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу (4.2) сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд q ₂ в начальной и конечной точках поля, создаваемого зарядом q ₁:

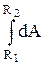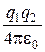
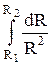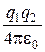
А₁₂ = = = = 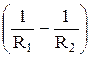W₁-W₂. (4.6)

Из анализа выражения (4.6) приходим к следующему соотношению для потенциальной энергии заряда q ₂ в поле заряда q ₁:

W= 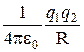+ const.

Значение константы в выражении потенциальной энергии обычно выбирается таким образом, чтобы при удалении заряда на бесконечность (т.е. при R®¥) потенциальная энергия обращалась в нуль. При этом условии получается, что потенциальная энергия равна

W= 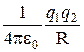. (4.7)

Для одноименных зарядов q ₁ q ₂ > 0 и потенциальная энергия их взаимодействия положительна, для разноименных зарядов q ₁ q ₂< 0 и потенциальная энергия их взаимодействия отрицательна.

Воспользуемся зарядом q ₂ в качестве пробного заряда для исследования поля (q _пр= q ₂). Согласно (4.7) потенциальная энергия, которой обладает пробный заряд, зависит не только от его величины q ₂, но и от величин q ₁ и R, определяющих поле. Следовательно, эта энергия может быть использована для описания поля подобно тому, как была использована для этой цели сила, действующая на пробный заряд.

Разные пробные заряды q ₂¢, q ₂¢ ¢ и т.д. будут обладать в одной и той же точке поля различной энергией W¢, W¢ ¢ и т.д. Однако отношение W/ q ₂, как видно из (4.7), будет для всех зарядов одним и тем же. Величина

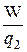j = (4.8)

называется потенциалом поля в данной точке и используется наряду с напряженностью поля для описания электрических полей.

Из (4.8) следует, что потенциал численно равен потенциальной энергии единичного положительного заряда в данной точке поля. Подставив в (4.8) значение потенциальной энергии (4.7), получим следующее выражение для потенциала j поля точечного заряда q = q ₁ (индекс 1 в произвольном случае можно опустить):

j = 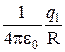= 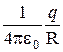. (4.9)

Если поле создается системой N точечных зарядов q ₁, q ₂,..., q _N, то работа электростатических сил, совершаемая над пробным зарядом равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия W пробного заряда q _пр, находящегося в этом поле, равна сумме его потенциальных энергий W_i, создаваемых каждым из зарядов в отдельности:

W= 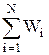= q _пр .

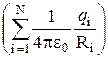Отсюда следует, что

j = 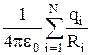. (4.10)

Сопоставление (4.10) и (4.9) приводит к заключению, что потенциал поля, создаваемого системой неподвижных точечных зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности в данной точке, т.е.

j= 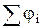. (4.11)

Выражение (4.11) определяет принцип суперпозиции для потенциала электрического поля. В то время как напряженности поля складываются при наложении полей векторно, потенциалы складываются алгебраически. По этой причине вычисление потенциалов оказывается обычно гораздо проще, чем вычисление напряженностей электрического поля.

Из формулы (4.8) вытекает, что заряд q, находящийся в точке с потенциалом j, обладает потенциальной энергией

W= q j. (4.12)

Следовательно, работа, совершаемая силами электростатического поля при перемещении заряда q из точки 1 в точку 2, может быть выражена через разность потенциалов:

А₁₂=W₁-W₂= q (j₁ - j₂). (4.13)

Таким образом, работа, совершаемая силами поля над зарядом, равна произведению величины перемещаемого заряда на разность потенциалов в начальной и конечной точках. Из сказанного следует, что физический смысл имеет только разность потенциалов или напряжение между двумя точками поля, так как работа определена только тогда, когда заданы две точки – начало и конец пути. Несмотря на это часто говорят просто о потенциале в данной точке, но всегда имеют в виду, разность потенциалов, подразумевая, что одна из точек выбрана заранее. Такую постоянную точку часто выбирают в «бесконечности», т.е. на достаточном удалении от всех заряженных тел, где потенциал по условию равен нулю.

Если заряд q удаляется из точки с потенциалом j на бесконечность, работа сил поля будет равна:

А_¥ = q j. (4.14)

Отсюда следует, что j =А_¥ / q, т.е. потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.

Из выражения (4.8) определяется единица потенциала - вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта, можно показать, что введенная в § 1.3 единица напряженности электростатического поля действительно равна 1 В/м: 1 Н/Кл = 1Н× м/(Кл× м) = 1Дж/(Кл× м) = 1 В/м.

В физике часто пользуются внесистемной единицей энергии и работы, называемой электронвольтом (эВ). Это такая энергия, которую приобретает частица с зарядом, равным элементарному заряду е =1, 6× 10^-19 Кл, пробегая в вакууме разность потенциалов (напряжение) 1 В:

1 эВ=1, 6× 10^-19 Кл× 1 В=1, 6× 10^-19 Дж. (4.15)

В электронвольтах обычно выражают энергию различных элементарных частиц (электронов, протонов и др.). При этом применяют также более крупные единицы:

1 кэВ (килоэлектронвольт) = 10³ эВ,

1 МэВ (мегаэлектронвольт) = 10⁶ эВ,

1 ГэВ (гигаэлектронвольт) = 10⁹ эВ.

Если известно распределение потенциала, т.е. его значение в каждой точке поля, то можно найти и напряженность этого поля в каждой точке.

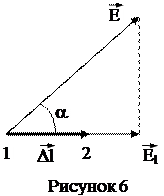
Рассмотрим в однородном электрическом поле две точки 1 и 2 и предположим, что единичный положительный заряд (q=+1) переходит из точки 1 в точку 2 вдоль отрезка прямой 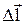(рисунок 6). Работу электрических сил А₁₂ при этом перемещении можно выразить через напряженность поля (см. (4.4)):

А₁₂ = q× E_l× Dl = E_l× Dl,

где E_l – проекция вектора напряженности на направление перемещения .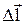

С другой стороны, ту же работу перемещения единичного положительного заряда можно выразить через разность потенциалов точек 1 и 2 (см. (4.13)):

А₁₂ = q× (j₁ - j₂)= j₁ - j₂.

Сравнивая оба выражения для работы, заключаем, что:

E_l× Dl = j₁ - j₂.

В последнем соотношении разность потенциалов поменяем на приращение потенциала, т.е. на Dj = j₂ - j₁ = - (j₁ - j₂), и получаем для напряженности электрического поля выражение:

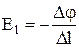. (4.16)

В общем случае неоднородного поля обе точки 1 и 2 нужно выбирать достаточно близко друг от друга, строго говоря, бесконечно близко, чтобы считать напряженность поля на отрезке Dl постоянной. Переходя в (4.16) к пределу при Dl®0, получим:

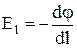. (4.17)

Производная, стоящая в правой части равенства (4.17), выражает быстроту изменения потенциала в данном направлении. Из этого равенства мы заключаем, что быстрота изменения потенциала в данном направлении равна проекции вектора напряженности на это направление с обратным знаком. Знак ² -² означает, что вектор направлен в сторону убывания потенциала j. Равенство (4.17) устанавливает связь между напряженностью электростатического поля (являющейся его силовой характеристикой) и потенциалом - энергетической характеристикой поля.

Из соотношения (4.17) можно получить выражение для работы перемещения единичного положительного заряда из точки 1 в точку 2, т.е. для разности потенциалов любых двух точек 1 и 2:

U₁₂ = j₁ - j₂ = 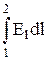, (4.18)

где интегрирование производится вдоль любого контура L, соединяющего рассматриваемые точки, в направлении от точки 1 к точке 2.

Если в электрическом поле перемещается не единичный заряд, а заряд величины q, то в каждой точке сила, действующая на заряд, увеличится в q раз. Поэтому работа А₁₂, совершаемая силами поля при перемещении заряда q из точки 1 в точку 2, равна

А₁₂ = qU₁₂, (4.19)

где величину U₁₂ часто называют напряжением между точками 1 и 2.

Из (4.19) следует, что работа определяется только через разность потенциалов или напряжение между двумя точками поля, т.е. работа определена только тогда, когда заданы две точки – начало и конец пути. Несмотря на это, часто говорят просто о потенциале или напряжении в данной точке, но всегда имеют в виду разность потенциалов, подразумевая, что одна из точек выбрана заранее. Такую постоянную точку часто выбирают «в бесконечности», т.е. на достаточном удалении от всех заряженных тел.

Преимущество использования потенциала для описания электрического поля заключается в том, что

- рассчитать распределение потенциала в пространстве значительно легче, чем распределение вектора напряженности,

- зная значения потенциала в двух точках по формуле (4.13) можно найти работу перемещения заряда между этими точками,

- зная распределение потенциала в пространстве, можно легко рассчитать напряженность поля в любой точке пространства,

- есть простые в исполнении приборы для измерения разности потенциалов (напряжения).

Для графического представления электрического поля удобно использовать так называемые эквипотенциальные поверхности или поверхности равного потенциала. Эквипотенциальная поверхность есть такая поверхность, на которой потенциал остается постоянным. Он может меняться только при переходе от одной эквипотенциальной поверхности к другой. Пользуясь эквипотенциальными поверхностями, можно изображать электрические поля графически, подобно тому, как это делают с помощью силовых линий. Пересекаясь с плоскостью чертежа, эквипотенциальные поверхности дают эквипотенциальные линии. Прочерчивая эквипотенциальные линии, соответствующие различным значениям потенциала, мы получаем наглядное представление о том, как изменяется потенциал в данном поле.

Силовые линии всегда перпендикулярны к эквипотенциальным поверхностям. Действительно, все точки эквипотенциальной поверхности имеют одинаковый потенциал, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т. е. электростатические силы, действующие на заряд, всегда направлены по нормалям к эквипотенциальным поверхностям. Следовательно, вектор всегда нормален к эквипотенциальным поверхностям, а поэтому линии вектора ортогональны этим поверхностям.

Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы зарядов можно провести бесчисленное множество. Однако их обычно проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше.

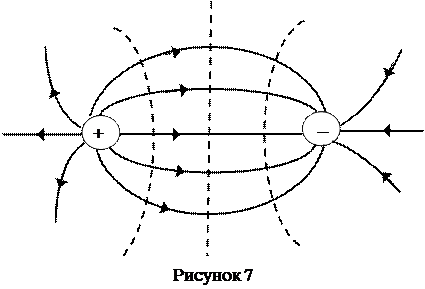Таким образом, зная расположение линий напряженности электростатического поля, можно построить эквипотенциальные поверхности и, наоборот, по известному расположению эквипотенциальных поверхностей можно всегда построить силовые линии данного поля. Поэтому любое электрическое поле можно графически изобразить при помощи эквипотенциальных поверхностей так же хорошо, как и при помощи силовых линий. На рисунке 7 для примера показан вид линий напряженности (сплошные линии) и эквипотенциальных поверхностей (пунктирные линии) поля двух разноименно заряженных металлических шаров.

В отсутствие электрического тока все точки проводника имеют одинаковый потенциал. Это значит, что в отсутствие тока поверхность проводника есть одна из его эквипотенциальных поверхностей и вектор напряженности электрического поля направлен нормально к его поверхности. Отсюда следует, что для перемещения какого-либо заряда из любой точки проводника в любую другую его точку не требуется никакой работы, т.е. разность потенциалов любых двух точек внутри проводника равна нулю. При этом заряды в проводнике находятся в равновесии, и напряженность поля внутри проводника равна нулю, т.е. =0.