Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Уравнение Лауэ. Сфера Эвальда

Условие получения дифракции рентгеновских лучей и электронов на кристалле описывается в разных моделях уравнениями Вульфа-Брэгга и Лауэ. Уравнение Вульфа-Брэгга

2d sin Θ = n λ, (8)

где d_(hkl) – расстояние между плоскостями (hkl) в кристалле, λ – длина волны излучения, n – порядок отражения, целое число.

Из (8) следует, что от одной и той же системы плоскостей можно получить отражения нескольких порядков при разных углах θ. Например, при n = 1 θ ₁ = arcsin(λ /2 d_hkl), при n = 2 θ ₂ == arcsin(λ / d_hkl). Ход лучей, соответствующих отражениям разного порядка от плоскости (hkl), показан на рис. 10. При λ > 2 d_hkl отсутствуют отражения даже первого порядка. Максимальная величина n определяется выражением n < 2 d_hkl /λ.

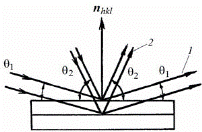
Рис. 10. Отражения первого (1) и второго (2) порядков от плоскости (hkl)

Необходимо подчеркнуть, что кристалл отражает рентгеновские лучи только при определенных углах скольжения θ, удовлетворяющих условию (8) и названных брэгговскими углами, т.е. в отличие от зеркал оптики видимого света кристалл отражает рентгеновские лучи селективно.

Формула Вульфа–Брэгга, как показали эксперименты, выполняется с достаточно большой точностью, и только при определении межплоскостных расстояний d_hkl с погрешностью Δ d_hkl < 10^–4 Å следует учитывать влияние преломления, приводящего к небольшому изменению углового положения дифракционного максимума.

Из формулы Вульфа–Брэгга следует, что, измеряя экспериментально угол θ дифракционного максимума, можно определить:

а) межплоскостное расстояние d_hkl, если известна длина волны λ, отвечающая дифракционному максимуму;

б) длину волны, отвечающую этому максимуму, при условии, что известно межплоскостное расстояние d_hkl.

Таким образом, формула Вульфа–Брэгга может быть использована только после определения стандартного межплоскостного расстояния, выполненного без применения этой формулы.

Уравнение Вульфа-Брэгга описывает дифракцию на кристалле в прямом пространстве. В обратном пространстве ему эквивалентно уравнение Лауэ:

(9)

где n ₀ и n ₁ - единичные вектора, нормальные к фронту распространения падающего и рассеянного лучей: |n₁| = |n₀| = 1;

в_qpr - вектор обратной решетки:

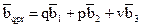, (10)

в ₁, в ₂, в ₃ - единичные трансляционные вектора обратной решетки, q, p, r – координаты узла обратного пространства.

Между индексами интерференции HKL, описывающими рефлекс (линию) на дифракционной картине, и координатами узлов обратного пространства [[ qpr ]] существует связь:

q = nh = H, p = nk = K, r = nl = L.

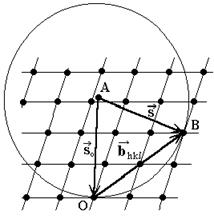
Рис. 11. Построение Эвальда.

Представление об обратной решётке облегчает интерпретацию явления дифракции. Для этого Эвальдом предложено графическое отображение уравнения Лауэ с помощью сферы, названной сферой распространения (сферой Эвальда) – рис. 11. Сфера Эвальда строится следующим образом:

1. Если плоскости прямой кристаллической решётки заменить векторами обратной решётки, то есть из одной точки (A) провести перпендикуляры к плоскостям { hkl } (векторы s₀ и s), то они являются векторами обратного пространства, абсолютная величина которых будет равна обратной величине приведенного межплоскостного расстояния: 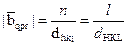, а углы между векторами в_qpr равны углам между плоскостями { hkl } прямого кристаллического пространства. Величина векторов обратной решётки и углы между ними определяют симметрию данной кристаллической структуры. При этом соотношения между плоскостями к ним сохраняются в независимости от их ориентировки по отношению к плоскости проекций, а пересечение векторов обратной решётки плоскостью проекций образует сетку из сечений узлов обратного пространства, конфигурация которых определяется формой отражающего кристалла.

2. В полученном сечении обратного пространства выбирается произвольно нулевой узел. Из нулевого узла в направлении обратном, по отношению к направлению падающего рентгеновского луча, откладывается вектор величиной 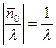, находится центр, из которого радиусом 1/λ описывается сфера Эвальда. Из уравнения Лауэ следует, что векторы, соединяющие центр сферы с узлами обратного пространства, расположенными на её поверхности, по абсолютной величине равны величине вектора | | по направлению падающего луча и соединяются с ним вектором обратной решётки в_qpr, т. е. в этом случае будет выполняться условие дифракции.

Таким образом, в отражающее положение попадают те плоскости кристаллической решётки, для которых узлы обратного пространства лежат на поверхности сферы Эвальда. По числу узлов, лежащих на поверхности сферы Эвальда, можно определить количество интерференционных максимумов (линий на дифракционной картине), найти их индексы интерференции HKL и углы Вульфа-Брэгга. При этом видно, что дифракция рентгеновских лучей происходит дискретно в определенных фиксированных направлениях.

Из этого анализа следует, что дифракционной характеристикой вещества является ряд значений межплоскостных расстояний d, а также относительных интенсивностей I отражений от этих плоскостей. Сведения о межплоскостных расстояниях d/n, относительных интенсивностей I и соответствующих им индексов интерференции HKL сводятся в таблицы, которые приводятся в справочниках. Каждая фаза имеет свою кристаллическую решётку, значит, характеризуется определенным набором межплоскостных расстояний. Поэтому для решения вопроса о том, какая фаза присутствует в исследуемом материале, достаточно рассчитать рентгенограмму или дифрактограмму, снятую по методу поликристалла, и сравнить полученный ряд межплоскостных расстояний с табличными значениями.

Рентгеноструктурный анализ позволяет установить симметрию, тип и периоды кристаллических решёток чистых веществ, химических и интерметаллических соединений, фаз, образующих сплавы, т. е. определить кристаллическую структуру веществ. Дифракция электронов на кристалле так же, как и дифракция рентгеновских лучей, описывается уравнением Лауэ. Однако в отличие от последних дифракция электронов описывается в пространстве волнового вектора К, которое отличается от обратного пространства только лишь

масштабом.

Волновой вектор К имеет вид 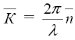, отсюда и уравнение Лауэ в обратном пространстве описывается в К пространстве выражением

где К ₁ - волновой вектор рассеянных электронных лучей; К ₀ - волновой вектор падающих электронных лучей; в_qpr - вектор обратной решётки, соединяющий волновые вектора К ₀ и К ₁.

Вследствие того, что длина волны электронов λ очень мала и составляет величину порядка 0, 04 Å (при напряжении на пушке электронного микроскопа ~80 кв), радиус сферы Эвальда – очень большая величина по сравнению с величиной вектора обратной решётки 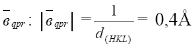(для дифракционного максимума (110) α -фазы на основе ОЦК решётки α -Fe).

Углы Вульфа-Брэгга для дифракции электронов на кристалле малы и составляют доли градуса. Поэтому уравнение Лауэ при дифракции электронов изображается графически как небольшой сегмент сферы Эвальда. Из этого следует, что вектор обратной решётки в_qpr лежит в плоскости, перпендикулярной падающему электронному лучу (рис. 11). Из этих соображений считается, что электрономограмма представляет собой плоское сечение обратного пространства, перпендикулярное падающему лучу электронов. Из сравнения подобных треугольников вытекает (рис. 12):

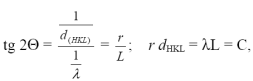(11)

где d _HKL - приведённое межплоскостное расстояние, Å или нм; r - расстояние от нулевого рефлекса до рефлекса с индексами HKL, мм; λ - длина волны электронов, [Å ]; L - расстояние от объекта до плоскости электронограммы, мм; С - электронографическая постоянная, Å *мм.

С помощью этого уравнения производится расчёт дифракционных картин в ПЭМ. Значение электронографической постоянной С находится из расчета электронограмм эталонных веществ, полученных в тех же условиях, что и электронограммы исследуемого объекта.

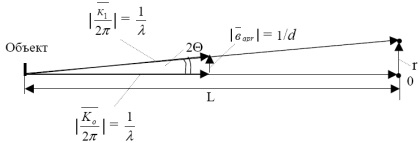
Рис. 12. Связь волновых векторов 1 K, 2 K и вектора обратной решётки