Понятие об обратной решетке

💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

4.1. Единичные трансляционные векторы обратной решётки

Обратная решетка – это математический образ, применяемый для установления соотношений между различными параметрами кристаллической решетки и величинами, определяющими то или иное физическое свойство кристалла.

Пространственная решетка кристалла, определяемая тремя векторами трансляции a₁, a₂, a₃ – называется прямой или атомной, так как в её узлах расположены атомы (молекулы, ионы);

С помощью определенных математических построений единичные векторы прямой решётки векторами обратной решетки b₁, b₂, b₃. Причем, прямой и обратный единичные векторы взаимно параллельны. С точностью до целого множителя вектор обратной решетки (характеризующий её узел) имеет те же индексы, что и плоскости прямой решетки, нормальные к нему. Следовательно, обратная решетка есть совокупность точек (узлов), каждая из которых отображает семейство параллельных атомных плоскостей и имеет те же индексы (с точностью до общего множителя).

Абсолютная величина вектора обратной решетки с индексами hkl равна обратной величине межплоскостного расстояния для плоскостей прямой решетки { hkl }.

Узлы обратной решетки строят из прямой решетки путем проведения из нулевого узла нормалей к соответствующим плоскостям. Длина нормали для каждого узла обратной решетки есть величина обратная межплоскостному расстоянию для соответствующих плоскостей. Представления об обратной решётке очень важны при решении структурных задач методом просвечивающей электронной микроскопии (ПЭМ), в большинстве из которых анализируется ориентация конкретных кристаллов, дающая дифракционный контраст на электронно-микроскопическом изображении. Определение ориентации тех или иных областей структуры в общем случае для кристаллов любой симметрии требует знания узлов разориентировки между направлениями и нормалями к одноимённым плоскостям. Только для кристаллов кубической симметрии нормали к плоскостям кристалла и одноименные направления совпадают. Анализ прямой и обратной решёток кристалла позволяет найти связь между плоскостями {hkl} и одноименными направлениями [hkl] для кристаллов любой симметрии.

Сначала рассмотрим кубические кристаллы. Прямая и обратная решётки в этом случае имеют одинаковую симметрию и отличаются друг от друга лишь объёмом. На рис. 8 представлена связь прямой и обратной кубических решёток на примере плоскостей {011} и направлений < 011>.

Рис. 8. Ориентация кристаллографических плоскостей и направлений в прямой и обратных решётках кристаллов кубической формы.

Таким образом, в кристаллах кубической симметрии одноименные плоскости прямой и обратной решёток, а также одноимённые направления в них совпадают:

В кристаллах более низкой симметрии, чем кубическая, плоскости и направления с одинаковыми индексами в прямой и обратной решётках находятся под углом друг к другу. Это явление рассмотрим на примере тетрагональной решётки (рис. 9), симметрия которой сохраняется в обратном пространстве.

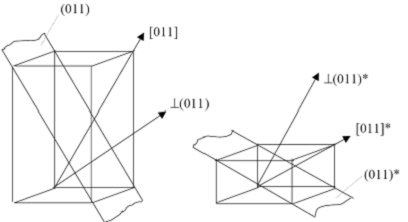
Рис. 9. Ориентация кристаллографических плоскостей и направлений в прямой и обратной решётках кристаллов тетрагональной формы.

а₁ = а₂ = а, а₃ = с; а, с – периоды прямой (кристаллической) тетрагональной решётки;

в₁ = в₂ = в =1/а; в₃ =1/с – периоды обратной тетрагональной решётки

Из сравнения элементарных ячеек прямой и обратной решёток, построенных с учетом их размеров, следует, что

Поскольку ориентация плоскости в пространстве может быть задана не только расположением лежащих в ней точек, но также и направлением нормали к этой плоскости, то введение понятия “обратной решетки” приводит по существу к тому, что задание ориентации плоскости в пространстве осуществляется с помощью её нормали, т.е. вектора обратной решетки. Нормаль обладает числом измерений на единицу меньшим, чем плоскость, что создает преимущество простоты, особенно в тех случаях, когда одновременно рассматривается совокупность большого числа плоскостей. Одновременно, в ряде случаев, при введении понятия обратной решетки упрощается и математическая интерпретация.