
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПЗ.8. Непрерывные законы распределения и их числовые характеристики.
|
|
Обратимся, прежде всего, к показательному распределению, которое мы уже начали обсуждать (см. формулу (П.3.14) в вопросе П.3.5) при рассмотрении распределения Пуассона, оценивающего вероятности событий, происходящих в простейшем потоке событий. Эти события происходят дискретно, но промежуток времени Т между двумя соседними событиями в простейшем потоке можно считать непрерывной величиной. Возникает задача определения вероятности того, что значение T < t, где t – время, прошедшее после предыдущего события (t > 0). Из соотношения (П.3.14) следует, что эта вероятность равна:
 , (П.3.28)
, (П.3.28)
где λ – параметр потока (см. формулу П.3.12).
Функцию (П.3.28) называют функцией показательного распределения вероятностей. Если интересующие нас события являются отказами оборудования, то P(T < 1), представленную соотношением (П.3.28), находим плотность распределения вероятностей величины Т:
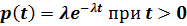 . (П.3.29)
. (П.3.29)
Математическое ожидание величины Т можно вычислить непосредственно по формуле (П.3.21):
 . (П.3.30)
. (П.3.30)
Если нас интересуют отказы оборудования, то формула (П.3.30) даёт среднюю наработку до отказа при условии, что λ – это удельная частота простейшего потока отказов.
Дисперсия показательного распределения согласно соотношению (П.3.23) равна:
 . (П.3.31)
. (П.3.31)
Следовательно, среднеквадратичное отклонение при показательном распределении равно математическому ожиданию.
Другим важнейшим законом распределения вероятностей является нормальный закон распределения, при котором плотность распределения случайной величины Х рассчитывается по формуле:
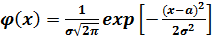 , (П.3.32)
, (П.3.32)
где σ – среднеквадратичное отклонение;
a – центр распределения (математическое ожидание).
После подстановки значений:
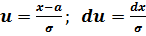
соотношение (П.3.32) примет вид стандартного нормального распределения с параметрами a = 0 и σ = 1:
 . (П.3.33)
. (П.3.33)
Чтобы найти функцию нормального распределения, необходимо взять интеграл от φ (u). Поскольку он не выражается через элементарные функции, то в расчётах, связанных с нормальным распределением, используются таблицы кратной данному интегралу функции:
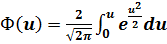 , (П.3.34)
, (П.3.34)
называемой интегралом вероятностей (табл.П.3.1). Ввиду нечёткости функции Ф(u) имеет место Ф(-u) = -Ф(u), что облегчает составление справочных таблиц. Согласно (П.3.34) вероятность попадания случайной величины U в любой интервал (u1, u2) составляет:
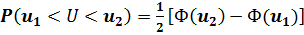 , (П.3.35)
, (П.3.35)
причём значения u вычисляются в соответствии с заданными пределами изменения исходной случайной величины Х:
 .
.
Таблица П.3.1
Интеграл вероятностей 
| u | Ф(u) | Ф(u1)-Ф(u2) | u | Ф(u) | Ф(u1)-Ф(u2) | u | Ф(u) | Ф(u1)-Ф(u2) |
| 0, 00 | 0, 0000 | 0, 0000 | 1, 00 | 0, 6827 | 0, 0248 | 2, 00 | 0, 9545 | 0, 0057 |
| 0, 05 | 0, 0399 | 0, 0399 | 1, 05 | 0, 7063 | 0, 0236 | 2, 05 | 0, 9596 | 0, 0051 |
| 0, 10 | 0, 0797 | 0, 0398 | 1, 10 | 0, 7287 | 0, 0224 | 2, 10 | 0, 9643 | 0, 0047 |
| 0, 15 | 0, 1192 | 0, 0395 | 1, 15 | 0, 7499 | 0, 0212 | 2, 15 | 0, 9684 | 0, 0041 |
| 0, 20 | 0, 1585 | 0, 0393 | 1, 20 | 0, 7699 | 0, 0200 | 2, 20 | 0, 9722 | 0, 0038 |
| 0, 25 | 0, 1974 | 0, 0389 | 1, 25 | 0, 7887 | 0, 0188 | 2, 25 | 0, 9756 | 0, 0034 |
| 0, 30 | 0, 2358 | 0, 0384 | 1, 30 | 0, 8064 | 0, 0177 | 2, 30 | 0, 9786 | 0, 0030 |
| 0, 35 | 0, 2737 | 0, 0379 | 1, 35 | 0, 8230 | 0, 0166 | 2, 35 | 0, 9812 | 0, 0026 |
| 0, 40 | 0, 3108 | 0, 0371 | 1, 40 | 0, 8385 | 0, 0155 | 2, 40 | 0, 9836 | 0, 0024 |
| 0, 45 | 0, 3473 | 0, 0365 | 1, 45 | 0, 8529 | 0, 0144 | 2, 45 | 0, 9857 | 0, 0021 |
| 0, 50 | 0, 3829 | 0, 0356 | 1, 50 | 0, 8664 | 0, 0135 | 2, 50 | 0, 9876 | 0, 0019 |
| 0, 55 | 0, 4177 | 0, 0348 | 1, 55 | 0, 8789 | 0, 0125 | 2, 55 | 0, 9892 | 0, 0016 |
| 0, 60 | 0, 4515 | 0, 0338 | 1, 60 | 0, 8904 | 0, 0115 | 2, 60 | 0, 9907 | 0, 0015 |
| 0, 65 | 0, 4843 | 0, 0328 | 1, 65 | 0, 9011 | 0, 0107 | 2, 65 | 0, 9920 | 0, 0013 |
| 0, 70 | 0, 5161 | 0, 0318 | 1, 70 | 0, 9109 | 0, 0098 | 2, 70 | 0, 9931 | 0, 0011 |
| 0, 75 | 0, 5467 | 0, 0306 | 1, 75 | 0, 9199 | 0, 0090 | 2, 75 | 0, 9940 | 0, 0009 |
| 0, 80 | 0, 5763 | 0, 0296 | 1, 80 | 0, 9281 | 0, 0082 | 2, 80 | 0, 9949 | 0, 0009 |
| 0, 85 | 0, 6047 | 0, 0284 | 1, 85 | 0, 9357 | 0, 0076 | 2, 85 | 0, 9956 | 0, 0007 |
| 0, 90 | 0, 6319 | 0, 0272 | 1, 90 | 0, 9426 | 0, 0069 | 2, 90 | 0, 9963 | 0, 0007 |
| 0, 95 | 0, 6579 | 0, 0260 | 1, 95 | 0, 9488 | 0, 0062 | 2, 95 | 0, 9968 | 0, 0005 |
Примечание. В столбцах 3. 6 и 9 приведены разности между приведёнными в строках значениями функции Ф(u). Они приведены для облегчения интерполяции. При линейной интерполяции ошибка не превышает 0, 0002 в интервале 0, 4 < u < 1, 8 и 0, 0001 в остальной части таблицы. Ошибка при расчёте вероятностей в целом не превышает 0, 0004.
Нормальный закон распределения характерен для процессов, в которых разброс параметров вызывается действием большого количества факторов, воздействие каждого из которых в отдельности трудно учесть ввиду его незначительности. Нормальное распределение характерно для распределения случайных ошибок измерений, разброса параметров производимой продукции и для многих других процессов производственного и непроизводственного характера. В частности, при испытаниях по схеме Бернулли, ведущих к биноминальному распределению (см. вопрос П.3.4), биноминальное распределение стремится к нормальному с увеличением числа испытаний n. Это позволяет в практических расчётах, в том числе в расчётах надёжности, применять формулы нормального распределения и тем значительно упростить расчёты.
|
|