
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПЗ.6. Непрерывные случайные величины. Плотность распределения вероятностей.
|
|
Расчёт вероятности случайной величины (события) Е базируется на подсчёте числа реализаций данного события в процессе испытаний (см. вопрос П.3.1) Критерии оценки реализации того или иного события всегда дискретны, так как ограничены снизу дискретностью принятой шкалы измерений (см. вопрос П.3.3). В тех случаях, когда можно пренебречь дискретностью измерений интересующей нас случайной величины Х, удобно представлять величину Х как изменяющуюся непрерывно в некотором интервале (α, β). Закон распределения вероятностей непрерывной случайной величины Х должен позволять находить вероятность её попадания в любой интервал (х1, х2) внутри интервала (α, β).
Для облегчения дальнейших рассуждений введём понятие функции случайной величины Х. Это такая случайная величина Y, которая принимает значение y = f(x) всякий раз, когда величина Х принимает значение х. Вероятность попадания величины Х в интервал (х1, х2) обозначим P(x1 < X < x2).
Будем считать, что вероятность попадания значения Х в интервал 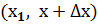 малой длины ∆ х > 0 пропорциональна ∆ х с точностью до бесконечно малых более высокого, чем ∆ х, порядка, т.е.:
малой длины ∆ х > 0 пропорциональна ∆ х с точностью до бесконечно малых более высокого, чем ∆ х, порядка, т.е.:
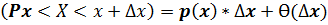 ,
,
или dP = p(x)*dx, причём Ө (∆ х)/∆ х→ 0, ∆ х→ dx при ∆ x→ 0.
Переходя к пределу при ∆ x→ 0, находим точное значение функции p(x):
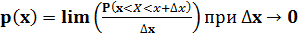 . (П.3.16)
. (П.3.16)
Функция p(x) есть плотность распределения вероятностей случайной величины Х.
Исходя из выражения (П.3.16) путём интегрирования элементов вероятности p(x)dx находим значение вероятности попадания случайной величины Х в любой интервал (х1, х2):
 . (П.3.17)
. (П.3.17)
Существование интервала (П.3.17) является доказательством непрерывности случайной величины Х. Если известно распределение P(x), то согласно (П.3.17) плотность распределения может быть найдена путём дифференцирования функции P(α < X < x) (где α – минимально возможное значение Х):
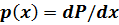 .
.
Функцию P(α < X < x) обычно отображают в виде P(X < x) и называют функцией распределения вероятности.
Если случайная величина Х существует лишь в интервале (α, β), то естественным нормирующим условием для функции p(x) является условие:
 ,
,
что соответствует достоверности ограничения значений величины Х интервалом (α, β).
|
|