Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПЗ.2. Основные свойства вероятностей.
|
|
Из соотношений (П.3.1) и (П.3.2) с учётом того, что 
, следует неравенство:
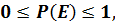
т.е. вероятность случайного события заключена между 0 и 1.
Если всегда имеет место nE = n, то P(E) = 1. Событие, вероятность которого равна единице, называется достоверным, а событие, вероятность которого равна нулю (P(E) = 0, nE = 0), называется невозможным.
Суммой событий A и B называют такое событие С, которое заключается в осуществлении хотя бы одного из них в одном и том же испытании. Если события A и B не могут произойти вместе при одном и том же испытании, то они называются несовместимыми. Вероятность суммы n попарно несовместимых событий равна сумме вероятностей этих событий:
. (П.3.3)
Случайные события образуют полную группу, если они попарно несовместимы, но при каждом повторении испытаний обязательно происходит одно из них, что приводит к тому, что сумма вероятностей событий, образующих полную группу, равна единице.
Два случайных события называются противоположными, если реализация одного из них гарантирует неосуществление другого. Противоположные события образуют полную группу, следовательно:
(П.3.4)
где P(Ā) – вероятность события Ā, противоположного событию А.
Произведением двух случайных событий называется произведение вероятности одного из них на условную вероятность другого, причём условной вероятностью P(B|A) называют вероятность события B при условии осуществления события А. формула произведения вероятностей, которое трактуется как вероятность совмещения двух событий, выглядит следующим образом:
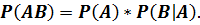(П.3.5)
Из формулы (П.3.5) следует формула вероятности суммы двух совместимых событий A и B, т.е. таких, у которых 
:
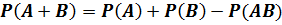. (П.3.6)
Если условные вероятности случайных событий равны их безусловным вероятностям, то такие события называются независимыми. Вероятность совмещения (или совпадения) независимых событий определяется произведением вероятностей составляющих событий:
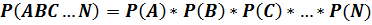(П.3.7)
|
|