Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Для односторонних (необратимых) реакций

В реакциях нулевого порядка скорость реакции от концентрации не зависит:

или 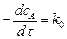. (5.2)

Это имеет место в тех случаях, когда убыль вещества в результате протекания химической реакции восполняется доставкой его из другой фазы или, если скорость процесса лимитируется подачей энергии, необходимой для активации реагирующих молекул. Нулевой порядок часто наблюдается в каталитических реакциях, когда скорость определяется концентрацией катализатора и не зависит от концентрации реагирующих веществ.

После интегрирования (5.2) получают

, (5.3)

откуда видно, что концентрация реагирующего вещества линейно убывает со временем. Единица измерения константы скорости совпадает с единицей измерения скорости. Подставляя в (5.3) , определяют время, за которое прореагирует половина исходного вещества, (период полупревращения):

.

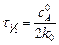Реакция первого порядка – А ® продукты.

Скорость реакции

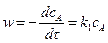. (5.4)

Уравнением первого порядка могут описываться скорости мономолекулярных реакций (изомеризация, термическое разложение и др.), а также ряда реакций с более сложным механизмом, например, гидролиза сахарозы с образованием фруктозы и глюкозы. Эта реакция бимолекулярная, однако, из-за наличия большого избытка воды скорость зависит только от концентрации сахарозы.

После интегрирования (5.4) находят

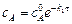, (5.5)

где 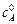– концентрация вещества А при t = 0.

Период полупревращения

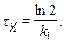
Единица измерения константы скорости реакции первого порядка – с^-1.

Реакция второго порядка – 2А ® продукты.

Скорость реакции

.

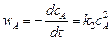После интегрирования:

. (5.6)

Период полупревращения:

.

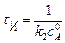Единица измерения константы скорости реакции второго порядка – м³/(моль× с).

Реакция второго порядка – А + В ® продукты.

Скорость реакции

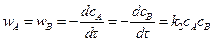. (5.7)

После интегрирования

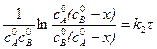. (5.8)

Период полупревращения как понятие не определяется.

Единица измерения константы скорости в этом случае – м³/(моль× с).

Реакция n -го порядка: А₁ + А₂ + А₃ … ® продукты.

При 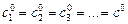скорость реакции равна

.

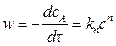После интегрирования:

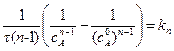. (5.9)

Если с=с ⁰/2, то

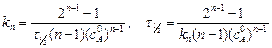. (5.10)

Время полупревращения реакции n -го порядка обратно пропорционально начальной концентрации реагентов в степени (n - 1).

Единица измерения константы скорости реакции в этом случае – (моль/м³)^1-n× с^-1.

Влияние температуры на константу скорости реакции

Скорость большинства гомогенных реакции увеличивается в 2-4 раза при повышении температуры на каждые 10 градусов (правило Вант-Гоффа).

Зависимость константы скорости одностадийной необратимой реакции от температуры описывается уравнением Аррениуса

,

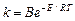где В – постоянная; Е – энергия активации реакции.

В логарифмической форме уравнение Аррениуса имеет вид

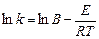. (5.11)

Под энергией активации понимают тот избыток энергии по сравнению со средней энергией молекул при данной температуре, которой должны обладать молекулы, чтобы они могли вступить в реакцию. Энергию активации обычно относят к 1 моль вещества. Из уравнения (5.11) следует, что между логарифмом константы скорости реакции и обратной температурой существует линейная зависимость.

В дифференциальной форме уравнение Аррениуса имеет вид

. (5.12)

Это соотношение позволяет установить связь между энергиями активации прямой и обратной реакций и изменением
энтальпии (или внутренней энергии). Для этого в уравнении изобары реакции

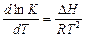
константу равновесия K выражают через отношение констант скоростей прямой k ₁и обратной k₂ реакций:

.

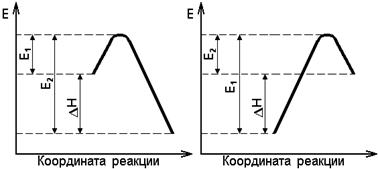
С учетом (5.12) получают (рис. 5.1):

а б

Рис. 5.1. Соотношения между энергиями активации

прямой Е ₁ и обратной Е ₂ реакций и изменением энтальпии:

а – экзотермическая реакция; б – эндотермическая реакция

Энергия активации может быть рассчитана с использованием графической зависимости (5.11) ln k=f (1/T), по формуле

,

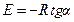где tga – тангенс угла наклона прямой линии.

Для определения энергии активации может быть использовано уравнение:

, (5.13)

где k ₁ и k ₂ – константы скорости при температурах Т ₁ и Т ₂ соответственно.