
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Каноническая форма Жордана
|
|
Определение 1. 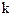 -мерной жордановой клеткой, соответствующей числу l называется треугольная матрица вида
-мерной жордановой клеткой, соответствующей числу l называется треугольная матрица вида
 .
.
Определение 2. Говорят, что матрица 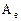 линейного оператора действующего в
линейного оператора действующего в 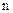 - мерном пространстве имеет нормальную жорданову форму, если вдоль ее главной диагонали расположены жордановы клетки, а остальные элементы нули
- мерном пространстве имеет нормальную жорданову форму, если вдоль ее главной диагонали расположены жордановы клетки, а остальные элементы нули
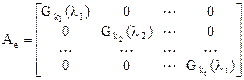 ,
,
где 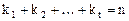 , а
, а 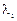 - собственные значения оператора. Не исключена возможность, что в матрице для некоторых номеров
- собственные значения оператора. Не исключена возможность, что в матрице для некоторых номеров 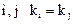 или
или 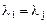 .
.
Базис пространства Х, в котором матрица оператора А имеет нормальную жорданову форму, называется каноническим.
В 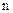 - мерном комплексном пространстве для каждого линейного оператора А существует базис, в котором матрица имеет нормальную жорданову форму. При переходе к другому каноническому базису матрица оператора сохраняется с точностью до перестановки клеток. Нормальная жорданова форма является простейшей формой, к которой может быть приведена матрица произвольного оператора.
- мерном комплексном пространстве для каждого линейного оператора А существует базис, в котором матрица имеет нормальную жорданову форму. При переходе к другому каноническому базису матрица оператора сохраняется с точностью до перестановки клеток. Нормальная жорданова форма является простейшей формой, к которой может быть приведена матрица произвольного оператора.
Построение нормальной жордановой формы состоит из следующих этапов:
1. Составляется и решается характеристическое уравнение 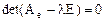 , определяются собственные значения оператора
, определяются собственные значения оператора 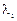 и их кратности
и их кратности 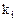 .
.
2. Для каждого собственного значения 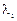 подсчитывается число соответствующих ему жордановых клеток
подсчитывается число соответствующих ему жордановых клеток 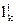 различной размерности
различной размерности 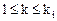 по формуле:
по формуле:
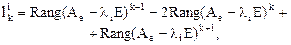
где  - ранг матрицы
- ранг матрицы 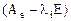 . Простым собственным значениям соответствуют жордановы клетки единичной размерности.
. Простым собственным значениям соответствуют жордановы клетки единичной размерности.
3. После того, как число клеток разной размерности, соответствующих различным собственным значениям определено, записывается нормальная жорданова форма с точностью до перестановки клеток. Канонический базис при этом остается неопределенным.
Пример. Привестик нормальной жордановой форме матрицу оператора:
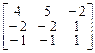 .
.
Для нахождения собственных значений оператора составим и решим характеристическое уравнение
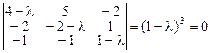 .
.
Откуда собственное значение 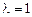 и его кратность
и его кратность  .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Определим теперь число жордановых клеток разной размерности. В нашем случае возможны три ситуации:
1. Существует три одномерных клетки.
2. Существует одна одномерная клетка и одна двумерная клетка.
3. Существует одна трехмерная клетка.
Сосчитаем число одномерных клеток:
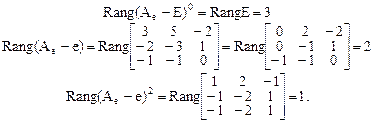
Поэтому количество одномерных клеток 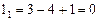 . Следовательно, возможен только третий вариант и нормальная жорданова форма матрицы оператора имеет вид
. Следовательно, возможен только третий вариант и нормальная жорданова форма матрицы оператора имеет вид
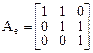 .
.
5.1. Задачи.
Привести к нормальной жордановой форме матрицы линейных операторов:
1. 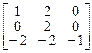 . 2.
. 2. 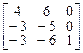 . 3.
. 3. 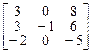 .
.
4. 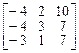 . 5.
. 5. 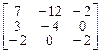 . 6.
. 6. 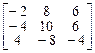 .
.
7. 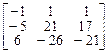 . 8.
. 8. 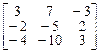 . 9.
. 9. 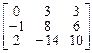 .
.
6. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВЫХ И УНИТАРНЫХ ПРОСТРАНСТВАХ.
6.1. Нормальный оператор.
Наличие ортонормированного базиса в унитарном пространстве и базиса из собственных векторов линейного оператора имеют принципиальное значение при выполнении различных исследований. Поэтому основной задачей при рассмотрении линейных операторов в унитарных пространствах является изучение того класса операторов, которые в унитарном пространстве имеют ортонормированный базис из собственных векторов.
Определение 1. Пусть 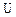 - произвольное унитарное пространство и
- произвольное унитарное пространство и 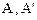 - операторы, действующие в
- операторы, действующие в 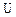 . Оператор
. Оператор 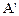 называется сопряженным к линейному оператору А, если
называется сопряженным к линейному оператору А, если
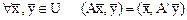 ,
,
где 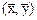 - скалярное произведение вектора
- скалярное произведение вектора 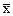 на вектор
на вектор 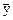 .
.
Для всякого линейного оператора А существует единственный линейный сопряженный оператор 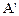 . Их матрицы в любом ортонормированном базисе пространства
. Их матрицы в любом ортонормированном базисе пространства 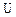 связаны соотношением
связаны соотношением
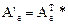 .
.
Определение 2. Линейный оператор А, действующий в 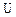 , называется нормальным, если он перестановочен со своим сопряженным оператором, т. е.
, называется нормальным, если он перестановочен со своим сопряженным оператором, т. е.
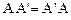 .
.
Оказывается, что оператор А имеет ортонормированный базис из собственных векторов тогда и только тогда, когда он является нормальным. При этом ортонормированные системы собственных векторов операторов А и 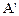 совпадают, а собственные значения, соответствующие одному и тому же собственному вектору, комплексно сопряжены.
совпадают, а собственные значения, соответствующие одному и тому же собственному вектору, комплексно сопряжены.
Частными случаями нормальных операторов являются:
1. Унитарный оператор, для которого 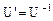 или
или 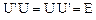 . Оператор
. Оператор 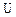 является унитарным тогда и только тогда, когда
является унитарным тогда и только тогда, когда
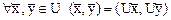 .
.
Все собственные значения унитарного оператора по модулю равны 1. Всякая ортонормированная система векторов пространства переводится унитарным оператором в ортонормированную систему векторов. Матрица унитарного оператора удовлетворяет условию
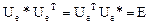 .
.
Такие матрицы называются унитарными.
В случае вещественного евклидова пространства 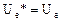 и матрица унитарного (ортонормированного) оператора удовлетворяет соотношению
и матрица унитарного (ортонормированного) оператора удовлетворяет соотношению
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
 .
.
Таким образом, столбцы данной матрицы ортонормированны. Например, ортонормированной матрицей второго порядка является следующая матрица
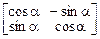 .
.
2. Самосопряженный оператор. Этот оператор совпадает со своим сопряженным, т. е.
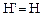 .
.
Матрица самосопряженного оператора удовлетворяет условию
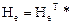 .
.
Такие матрицы называются эрмитовыми. Все собственные значения самосопряженного оператора вещественны.
В случае евклидова пространства самосопряженный оператор переходит в симметричный оператор, матрица которого является симметричной, т. е.
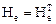 .
.
Определение 3. Самосопряженный оператор Н называется положительно (неотрицательно) определенным, если
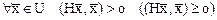 .
.
Всякий самосопряженный оператор положительно определен тогда и только тогда, когда его собственные значения положительны. Для любого оператора А операторы 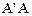 и
и 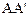 являются неотрицательно определенными.
являются неотрицательно определенными.
6.2. Приведение матрицы нормального оператора к диагональному виду
Так как для всякого нормального оператора существует ортонормированный базис из собственных векторов, то матрица всякого нормального оператора может быть приведена к диагональному виду соотношением
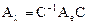 .
.
Все отличие от общего случая состоит в том, что теперь матрица перехода С (матрица из координат собственных векторов) должна быть выбрана так, чтобы ее столбцы были ортонормированны, т. е. теперь С – унитарная матрица. Тогда общее соотношение перепишется в виде
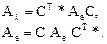
Полезно помнить, что всякий матричный многочлен
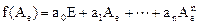
от матрицы 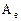 имеет те же собственные векторы, что и матрица
имеет те же собственные векторы, что и матрица 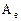 , а соответствующие собственные значения равны
, а соответствующие собственные значения равны
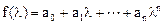 .
.
Например, матрица
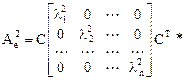 .
.
Пример. Найти ортонормированный базис из собственных векторов и матрицу  в этом базисе для линейного оператора, заданного в некотором ортонормированном базисе матрицей
в этом базисе для линейного оператора, заданного в некотором ортонормированном базисе матрицей
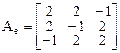 .
.
Матрица 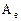 является симметричной, поэтому искомый базис заведомо существует. Для нахождения собственных значений составляем и решаем характеристическое уравнение
является симметричной, поэтому искомый базис заведомо существует. Для нахождения собственных значений составляем и решаем характеристическое уравнение
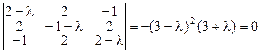 ,
,
откуда собственные значения 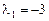 кратности
кратности 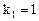 и
и 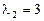 кратности
кратности  . Поэтому диагональная матрица оператора в базисе из собственных векторов
. Поэтому диагональная матрица оператора в базисе из собственных векторов
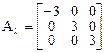 .
.
Для нахождения базиса составляем и решаем системы уравнений 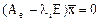 . При
. При 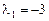 имеем
имеем
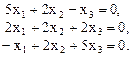
Нормированное решение этой системы вектор
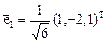 .
.
При 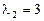 имеем
имеем
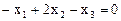 .
.
Линейно независимые решения этого уравнения
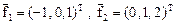 .
.
Применяя к векторам 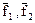 процедуру ортогонализации Грама–Шмидта, получим еще два ортонормированных собственных вектора
процедуру ортогонализации Грама–Шмидта, получим еще два ортонормированных собственных вектора
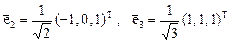 .
.
Тогда матрица перехода С имеет вид
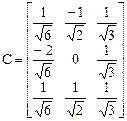 .
.
6.3. Полярное разложение оператора
Если А – произвольный линейный оператор, действующий в унитарном пространстве 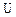 , то существует единственный неотрицательный самосопряженный оператор
, то существует единственный неотрицательный самосопряженный оператор 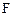 и унитарный оператор
и унитарный оператор 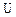 такие, что
такие, что
 .
.
Оператор 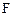 определяется из условия
определяется из условия 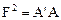 , т. е. является арифметическим корнем из оператора
, т. е. является арифметическим корнем из оператора 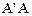 . Оператор
. Оператор 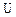 является единственным лишь тогда, когда оператор А невырожден. В этом случае
является единственным лишь тогда, когда оператор А невырожден. В этом случае 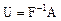 . Для нормального оператора А операторы
. Для нормального оператора А операторы 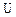 и
и 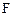 перестановочны.
перестановочны.
Пример. Построим полярное разложение оператора, который задан матрицей
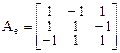 .
.
Матрица сопряженного оператора имеет вид
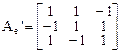
и матрица оператора 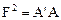 тогда равна
тогда равна
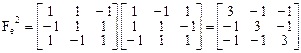 .
.
Для построения матрицы 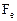 необходимо найти собственные векторы и собственные значения матрицы
необходимо найти собственные векторы и собственные значения матрицы 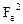 . Решим соответствующее характеристическое уравнение
. Решим соответствующее характеристическое уравнение
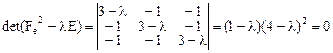 .
.
Откуда собственные значения 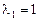 кратности
кратности 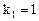 и
и 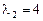 кратности
кратности  .
.
Координаты первого собственного вектора, соответствующего 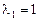 , определятся системой
, определятся системой
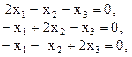
нормированное решение которой, например, вектор 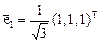 .
.
Координаты второго и третьего собственных векторов, соответствующих 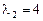 , определяются уравнением
, определяются уравнением
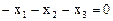 ,
,
имеющего два линейно независимых решения, например, векторы 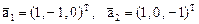 . Применяя к векторам
. Применяя к векторам 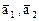 процедуру ортогонализации Грама–Шмидта, получим еще два ортонормированных собственных вектора
процедуру ортогонализации Грама–Шмидта, получим еще два ортонормированных собственных вектора
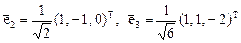 .
.
Ортонормированная матрица перехода тогда равна
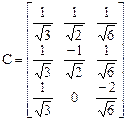 .
.
Матрицы 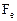 и
и 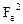 имеют одни и те же собственные векторы и собственные значения
имеют одни и те же собственные векторы и собственные значения 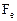 - корни из собственных значений
- корни из собственных значений 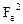 . Поэтому
. Поэтому
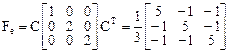 .
.
Далее, 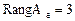 , т. е.
, т. е. 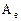 - невырожденная матрица. Поэтому матрица
- невырожденная матрица. Поэтому матрица 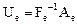 . Учитывая, что собственные значения
. Учитывая, что собственные значения 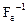 обратны собственным значениям
обратны собственным значениям 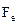 , получим
, получим
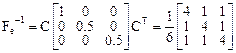 ,
,
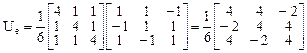 .
.
Непосредственным умножением нетрудно убедиться теперь, что 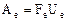 .
.
6.4. Задачи
1. Доказать, что сопряженные операторы обладают следующими свойствами:
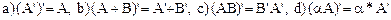
2. Для линейных операторов, заданных следующими матрицами, найти матрицы сопряженных операторов:
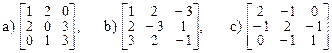 .
.
3. Проверить, являются ли нормальными операторы, заданные в некотором трехмерном унитарном пространстве матрицами из задачи 2.
Найти ортонормированный базис из собственных векторов и матрицу  в этом базисе для линейных операторов, заданных в некотором ортонормированном базисе матрицами:
в этом базисе для линейных операторов, заданных в некотором ортонормированном базисе матрицами:
4. 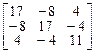 . 5.
. 5. 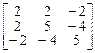 . 6.
. 6. 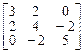 .
.
7. 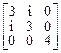 .
.
Найти полярное разложение следующих матриц:
8. 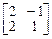 . 9.
. 9. 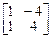 . 10.
. 10. 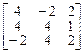 .
.
Найти собственные значения матричного многочлена 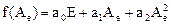 , если матрица
, если матрица 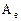 равна:
равна:
11. 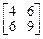 . 12.
. 12. 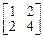 . 13.
. 13. 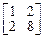 .
.
7. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
Определение 1. Числовая функция 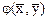 двух векторных аргументов
двух векторных аргументов 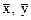 , определенная на комплексном пространстве Х, называется билинейной формой, если при каждом фиксированном
, определенная на комплексном пространстве Х, называется билинейной формой, если при каждом фиксированном 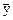 она линейна по
она линейна по 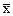 , а при каждом фиксированном
, а при каждом фиксированном 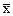 сопряженно - линейна по
сопряженно - линейна по 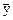 , т. е.
, т. е.
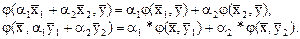
Если в пространстве Х задан базис 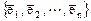 и
и 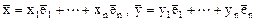 , то значение билинейной формы равно
, то значение билинейной формы равно
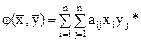 ,
,
где  - значение билинейной формы на паре базисных векторов. Матрица
- значение билинейной формы на паре базисных векторов. Матрица 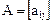 называется матрицей билинейной формы в заданном базисе Х. В матричных обозначениях
называется матрицей билинейной формы в заданном базисе Х. В матричных обозначениях
 ,
,
где 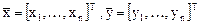 .
.
Если два базиса пространства 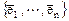 и
и 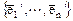
связаны формулами перехода
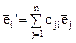 ,
,
где 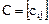 - матрица перехода, то матрицы А и
- матрица перехода, то матрицы А и 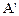 билинейной формы в этих базисах связаны соотношением
билинейной формы в этих базисах связаны соотношением
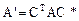
Ранг матрицы билинейной формы называется рангом билинейной формы. При переходе от базиса к базису ранг билинейной формы не меняется.
Билинейная форма 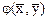 , определенная на комплексном пространстве, называется эрмитовой, если
, определенная на комплексном пространстве, называется эрмитовой, если 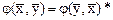 .Эрмитовой форме соответствует эрмитова матрица А, для которой
.Эрмитовой форме соответствует эрмитова матрица А, для которой 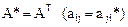 .
.
При 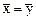 билинейная форма
билинейная форма 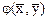 переходит в квадратичную форму
переходит в квадратичную форму 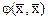 . В
. В 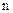 - мерном пространстве всякая квадратичная форма имеет вид
- мерном пространстве всякая квадратичная форма имеет вид
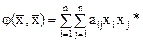 .
.
Квадратичная форма с эрмитовой матрицей принимает только действительные значения.
7.1. Приведение квадратичной формы к каноническому виду
Основная задача, связанная с квадратичными формами, состоит в приведении ее с помощью линейного невырожденного преобразования переменных (преобразования базиса) к максимально простому (каноническому) виду.
Определение 2. Каноническим видом эрмитовой квадратичной формы называется выражение вида
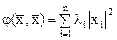 ,
,
где 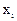 - координаты вектора
- координаты вектора 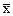 , а
, а 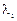 - вещественные канонические коэффициенты.
- вещественные канонические коэффициенты.
7.1.1. Метод Лагранжа
Метод Лагранжа позволяет привести к каноническому виду симметрическую вещественную квадратичную форму. Идея метода состоит в последовательном дополнении квадратного многочлена по каждой переменной до полного квадрата.
Пусть
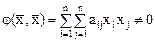 .
.
Будем считать, что 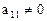 . Если это не так, то возможны два варианта:
. Если это не так, то возможны два варианта:
1. Какой–нибудь из 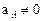 . Тогда перенумеровав базисные векторы (переобозначение переменных), получим требуемое условие.
. Тогда перенумеровав базисные векторы (переобозначение переменных), получим требуемое условие.
2. Если все 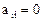 , и, например,
, и, например, 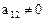 , то сделаем следующее невырожденное преобразование
, то сделаем следующее невырожденное преобразование
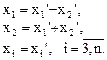
При этом 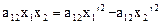 и коэффициент при
и коэффициент при 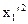
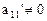 .
.
Выделим в выражении для 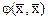 слагаемые, содержащие
слагаемые, содержащие  :
:
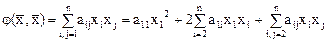 .
.
Преобразуем слагаемые с  :
:
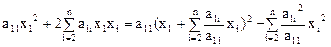 .
.
Сделаем невырожденное преобразование переменных
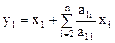 ,
,
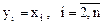 .
.
Обозначим 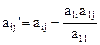 . Тогда для
. Тогда для 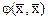 получим
получим
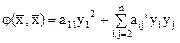 .
.
Если теперь квадратичная форма
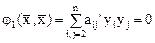 ,
,
то 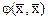 приведена к каноническому виду. Если
приведена к каноническому виду. Если 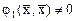 , то, проводя аналогичные преобразования координат
, то, проводя аналогичные преобразования координат 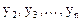 , за конечное число шагов приведем квадратичную форму к каноническому виду.
, за конечное число шагов приведем квадратичную форму к каноническому виду.
Пример. Приведем к каноническому виду квадратичную форму
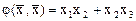 .
.
Здесь все 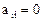 , а коэффициент
, а коэффициент 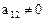 . Поэтому сделаем преобразование
. Поэтому сделаем преобразование
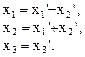
Тогда
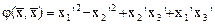 .
.
Выделим и преобразуем слагаемые с 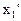 :
:
 .
.
Сделаем замену переменных
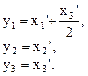
Тогда
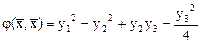 .
.
Преобразуем далее слагаемые с 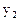 :
:
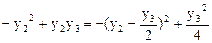
и сделаем замену переменных
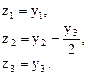
Квадратичная форма принимает канонический вид
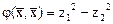 .
.
7.1.2. Метод Якоби
Метод Якоби позволяет найти канонические коэффициенты невырожденной эрмитовой квадратичной формы по ее коэффициентам в произвольном базисе, не строя сам канонический базис.
Обозначим через 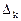 главный минор
главный минор 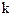 - го порядка матрицы квадратичной формы
- го порядка матрицы квадратичной формы 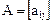 , т. е.
, т. е.
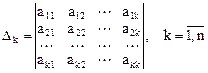 .
.
Если все главные миноры 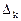 матрицы квадратичной формы отличны от нуля, то существует канонический базис, в котором данная форма имеет вид
матрицы квадратичной формы отличны от нуля, то существует канонический базис, в котором данная форма имеет вид
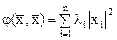 ,
,
где
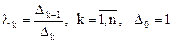 .
.
Пример. Приведем к каноническому виду методом Якоби квадратичную форму
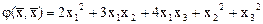 .
.
Матрица квадратичной формы
 .
.
Главные миноры матрицы
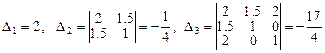 .
.
Поэтому
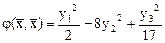 ,
,
где 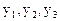 - координаты вектора
- координаты вектора 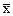 в каноническом базисе.
в каноническом базисе.
7.1.3.Приведение квадратичной формы к каноническому виду в ортонормированном базисе
Пусть 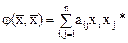 - эрмитова квадратичная форма, заданная в унитарном (евклидовом) пространстве. С помощью некоторого невырожденного линейного преобразования она может быть приведена к каноническому виду, причем выбор канонического базиса неоднозначен. Оказывается, что для эрмитовой квадратичной формы среди всех канонических базисов существует и ортонормированный базис.
- эрмитова квадратичная форма, заданная в унитарном (евклидовом) пространстве. С помощью некоторого невырожденного линейного преобразования она может быть приведена к каноническому виду, причем выбор канонического базиса неоднозначен. Оказывается, что для эрмитовой квадратичной формы среди всех канонических базисов существует и ортонормированный базис.
Так как 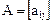 - матрица квадратичной формы является эрмитовой (самосопряженной), то она представима в виде
- матрица квадратичной формы является эрмитовой (самосопряженной), то она представима в виде
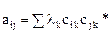 ,
,
где 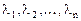 - собственные значения, а
- собственные значения, а 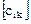 - ортонормированная матрица собственных векторов матрицы А. Введем новые переменные (новые координаты вектора
- ортонормированная матрица собственных векторов матрицы А. Введем новые переменные (новые координаты вектора 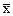 ) соотношениями
) соотношениями
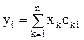 .
.
В новых переменных квадратичная форма
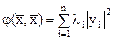 .
.
Таким образом, для приведения квадратичной формы к каноническому виду необходимо найти собственные значения матрицы А, которые и являются каноническими коэффициентами. Если нужна также связь между старыми и новыми координатами вектора 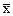 , то нужно найти ортонормированную матрицу собственных векторов.
, то нужно найти ортонормированную матрицу собственных векторов.
Пример. Найдем канонический вид в ортонормированном базисе квадратичной формы
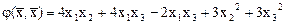 .
.
Матрица квадратичной формы
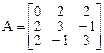 .
.
Для определения канонических коэффициентов составим и решим характеристическое уравнение
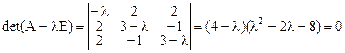 .
.
Откуда 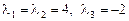 , и канонический вид квадратичной формы
, и канонический вид квадратичной формы
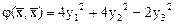 .
.
Найдем связь между старыми и новыми координатами вектора 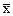 . Собственные векторы матрицы А при
. Собственные векторы матрицы А при 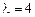 определяются уравнением
определяются уравнением
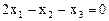 ,
,
линейно независимые решения которого, например, векторы
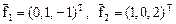 .
.
Координаты третьего собственного вектора определяются системой

которая имеет решение 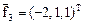 . Применяя к полученным векторам процесс ортогонализации Грама - Шмидта, получим искомый ортонормированный базис
. Применяя к полученным векторам процесс ортогонализации Грама - Шмидта, получим искомый ортонормированный базис
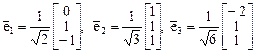 ,
,
и связь между старыми и новыми координатами вектора 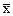
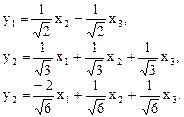
7.1.4. Задачи
Привести к каноническому виду методом Лагранжа следующие квадратичные формы:
1. 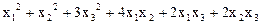 .
.
2. 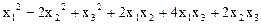 .
.
3. 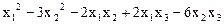 .
.
4. 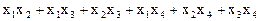 .
.
5. 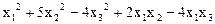 .
.
Привести к каноническому виду методом Якоби, если это возможно, следующие квадратичные формы:
6. 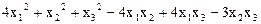 .
.
7. 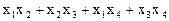 .
.
8. 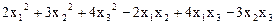 .
.
9. 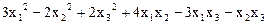 .
.
10. 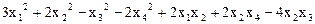 .
.
Найти ортогональное преобразование, приводящее следующие квадратичные формы к каноническому виду и записать этот вид.
11. 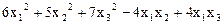 .
.
12. 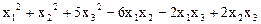 .
.
13. 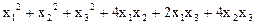 .
.
14. 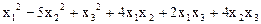 .
.
15. 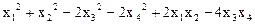 .
.
16. 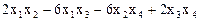 .
.
Найти канонический вид, к которому следующие квадратичные формы приводятся ортогональным преобразованием
17. 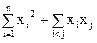 . 18.
. 18.  .
.
7.2. Знакоопределенные квадратичные формы
Определение. Эрмитова квадратичная форма 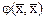 называется положительно (неотрицательно) определенной, если
называется положительно (неотрицательно) определенной, если
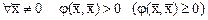 .
.
Эрмитова квадратичная форма 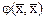 называется отрицательно (неположительно определенной), если
называется отрицательно (неположительно определенной), если
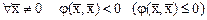 .
.
Для положительной (отрицательной) определенности квадратичной формы необходимо и достаточно, чтобы все ее канонические коэффициенты в произвольном базисе имели одинаковые знаки.
7.2.1. Матрица Грама
Пусть на комплексном пространстве Х заданы положительно определенная эрмитова квадратичная форма 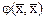 и соответствующая ей билинейная форма
и соответствующая ей билинейная форма 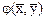 ,
, 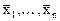 - конечная система векторов пространства Х.
- конечная система векторов пространства Х.
Определение. Матрица
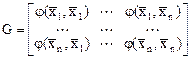
называется матрицей Грама данной системы векторов относительно формы 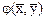 .
.
Матрица Грама системы векторов относительно положительно определенной эрмитовой формы 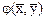 вырождена тогда и только тогда, когда эти векторы линейно зависимы.
вырождена тогда и только тогда, когда эти векторы линейно зависимы.
Очевидно, матрица 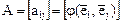 положительно определенной квадратичной формы
положительно определенной квадратичной формы 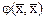 является матрицей Грама базисной системы векторов относительно
является матрицей Грама базисной системы векторов относительно 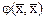 .
.
Пример. Определим в пространстве 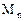 многочленов степени
многочленов степени 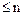 с действительными коэффициентами билинейную форму
с действительными коэффициентами билинейную форму 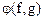 соотношением
соотношением
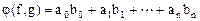 ,
,
где 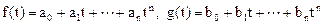 . Очевидно, соответствующая квадратичная форма
. Очевидно, соответствующая квадратичная форма 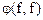 является положительно определенной. Построим матрицу Грама для системы многочленов
является положительно определенной. Построим матрицу Грама для системы многочленов
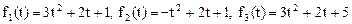 .
.
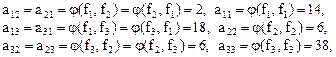
и матрица  имеет вид
имеет вид
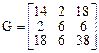 .
.
Вычислив определитель 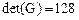 , убеждаемся, что многочлены
, убеждаемся, что многочлены 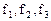 - линейно независимы.
- линейно независимы.
7.2.2. Критерий Сильвестра
Для того, чтобы эрмитова квадратичная форма была положительно определена, необходимо и достаточно, чтобы все главные миноры 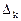 ее матрицы
ее матрицы 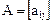 были положительны, т. е.
были положительны, т. е.
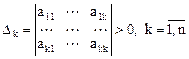 .
.
Пример. Найти все значения параметра 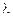 , при которых положительно определена квадратичная форма
, при которых положительно определена квадратичная форма
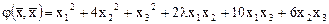 .
.
Матрица квадратичной формы
 .
.
Главные миноры матрицы
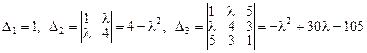 .
.
Согласно критерию Сильвестра, необходимо выполнение условий
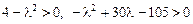 .
.
Решение первого неравенства 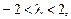 а решение второго
а решение второго 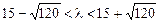 . Одновременное выполнение этих условий невозможно и, следовательно, квадратичная форма не является положительно определенной.
. Одновременное выполнение этих условий невозможно и, следовательно, квадратичная форма не является положительно определенной.
7.2.3. Одновременное приведение двух квадратичных форм к каноническому виду.
Пусть 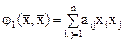 и
и 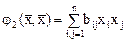 - симметричные квадратичные формы, заданные на вещественном пространстве, причем одна из них, например,
- симметричные квадратичные формы, заданные на вещественном пространстве, причем одна из них, например, 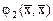 - положительно определена. Тогда существует преобразование переменных, одновременно приводящее эти квадратичные формы к сумме квадратов
- положительно определена. Тогда существует преобразование переменных, одновременно приводящее эти квадратичные формы к сумме квадратов
 ,
,
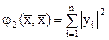 ,
,
где канонические коэффициенты 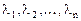 являются собственными значениями матрицы
являются собственными значениями матрицы 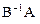 и могут быть определены как корни алгебраического уравнения
и могут быть определены как корни алгебраического уравнения 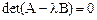 .
.
Пример. Привести к каноническому виду с помощью невырожденного преобразования пару квадратичных форм
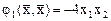 ,
,
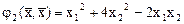 .
.
Матрицы данных форм соответственно равны
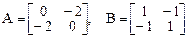 .
.
Используя, например, критерий Сильвестра, убеждаемся, что вторая квадратичная форма положительно определена. Поэтому задача имеет решение. Для нахождения канонических коэффициентов составляем и решаем уравнение
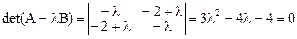 ,
,
корни которого 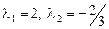 . Поэтому в каноническом базисе
. Поэтому в каноническом базисе 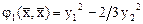 ,
, 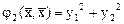 .
.
7.2.4. Задачи
Найти все значения параметра 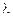 , при которых положительно определены квадратичная формы:
, при которых положительно определены квадратичная формы:
1. 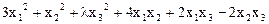 .
.
2. 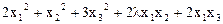 .
.
3. 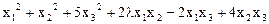 .
.
4. 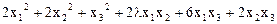 .
.
5. Пусть Х – множество непрерывных на интервале 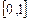 функций. Зададим на множестве Х билинейную форму
функций. Зададим на множестве Х билинейную форму
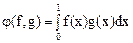 .
.
Показать, что 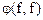 положительно определена. Построить матрицу Грама системы функций
положительно определена. Построить матрицу Грама системы функций 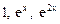 и доказать их линейную независимость.
и доказать их линейную независимость.
6. Доказать, что определитель матрицы Грама системы векторов  не изменится, если какой-либо вектор системы заменить перпендикуляром, опущенным из этого вектора на линейную оболочку любых других векторов системы.
не изменится, если какой-либо вектор системы заменить перпендикуляром, опущенным из этого вектора на линейную оболочку любых других векторов системы.
Выяснить, что в следующих парах квадратичных форм одна форма положительно определена и привести их одновременно к каноническому виду, не определяя канонический базис:
7. 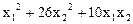 ,
,
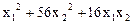 .
.
8. 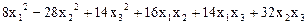 ,
,
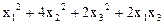 .
.
9. 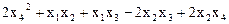 ,
,
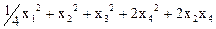 .
.
7.3 Поверхности второго порядка
Определение. Поверхностью второго порядка в пространстве 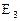 называется геометрическое место точек, координаты
называется геометрическое место точек, координаты 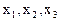 которых относительно ортонормированного базиса удовлетворяют уравнению
которых относительно ортонормированного базиса удовлетворяют уравнению
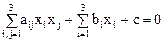 ,
,
где 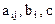 - вещественные числа.
- вещественные числа.
Исследование уравнения поверхности основано на приведении его к каноническому виду с помощью невырожденных преобразований координат. Обозначим 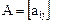 ,
, 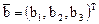 ,
, 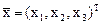 . Тогда уравнение поверхности примет вид
. Тогда уравнение поверхности примет вид
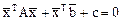 .
.
С помощью некоторого ортогонального преобразования квадратичную форму 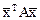 можно привести к каноническому виду
можно привести к каноническому виду
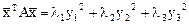 ,
,
где 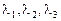 - собственные значения матрицы А,
- собственные значения матрицы А, 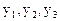 - координаты вектора
- координаты вектора 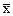 в ортонормированном базисе из собственных векторов матрицы А. В новых переменных уравнение поверхности примет вид
в ортонормированном базисе из собственных векторов матрицы А. В новых переменных уравнение поверхности примет вид
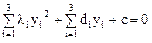 ,
,
где 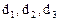 - новые координаты вектора
- новые координаты вектора 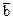 . Совершая далее параллельный перенос начала координат (если это необходимо), получим каноническое уравнение поверхности.
. Совершая далее параллельный перенос начала координат (если это необходимо), получим каноническое уравнение поверхности.
Пример. Определить вид поверхности, заданной в некотором ортонормированном базисе уравнением
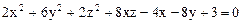 .
.
В нашем примере
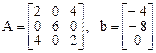 .
.
Приведем квадратичную форму 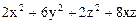 к каноническому виду. Для определения канонических коэффициентов составим и решим характеристическое уравнение
к каноническому виду. Для определения канонических коэффициентов составим и решим характеристическое уравнение
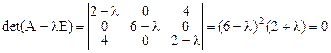 ,
,
откуда 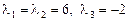 .
.
Найдем теперь канонический базис. При 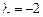 координаты собственных векторов матрицы А определяются системой
координаты собственных векторов матрицы А определяются системой
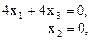
нормированное решение которой, например, вектор
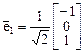 .
.
При 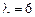 из системы
из системы
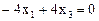
находим еще два ортонормированных базисных вектора

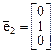 ,
, 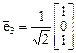 .
.
Определим новые координаты векторов 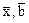 в построенном базисе следующими соотношениями:
в построенном базисе следующими соотношениями:
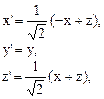
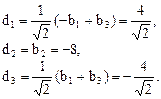
Уравнение поверхности в новом базисе примет вид
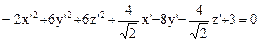 .
.
Перенесем начало координат, сделав замену переменных
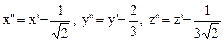 ,
,
и получим каноническое уравнение данной поверхности:

- уравнение двуполостного гиперболоида.
7.3.1. Задачи
1. 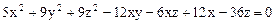 .
.
2.  .
.
3. 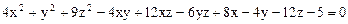 .
.
4. 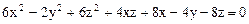 .
.
ЛИТЕРАТУРА
1. Воеводин В.В. Линейная алгебра. – М.: «Наука», 1974. – 400 с.
2. Ефимов Н.В., Розендрон Э.Р. Линейная алгебра и многомерная геометрия. – М.: «Наука», 1974. – 250 с.
3. Проскуряков И.В. Сборник задач по линейной алгебре. – М.: «Наука», 1970. – 355 с.
СОДЕРЖАНИЕ
1. Линейные операторы. Матрица линейного оператора 3
1.1. Определение оператора. Действия с операторами 3
1.2. Матрица линейного оператора 4
1.3. Задачи 7
2. Образ и ядро линейного оператора 9
2.1. Задачи 10
3. Собственные векторы и собственные значения
линейного оператора 10
3.1. Оператор простой структуры. Диагонализация
матрицы оператора 12
3.2. Задачи 14
4. Инвариантные подпространства 15
4.1. Задачи 17
5. Каноническая форма Жордана 18
5.1. Задачи 21
6. Линейные операторы в евклидовых и унитарных
пространствах 21
6.1. Нормальный оператор 21
6.2. Приведение матрицы нормального оператора
к диагональному виду 23
6.3. Полярное разложение оператора 25
6.4. Задачи 28
7. Билинейные и квадратичные формы 29
7.1. Приведение квадратичной формы к
каноническому виду 30
7.1.1. Метод Лагранжа 31
7.1.2. Метод Якоби 33
7.1.3. Приведение квадратичной формы к
каноническому виду в ортонормированном
базисе 34
7.1.4. Задачи 36
7.2. Знакоопределенные квадратичные формы 37
7.2.1. Матрица Грама 38
7.2.2. Критерий Сильвестра 39
7.2.3. Одновременное приведение двух
квадратичных форм к каноническому виду 40
7.2.4. Задачи 41
7.3. Поверхности второго порядка 42
7.3.1. Задачи 44
Литература 44
|
|
