
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Образ и ядро линейного оператора
|
|
Определение 1. Образом 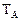 линейного оператора А называется множество всех элементов
линейного оператора А называется множество всех элементов 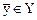 , представимых в виде
, представимых в виде 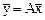 , где
, где 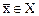 .
.
Образ 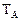 линейного оператора А является линейным подпространством пространства
линейного оператора А является линейным подпространством пространства 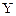 . Его размерность
. Его размерность 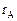 называется рангом оператора А.
называется рангом оператора А.
Определение 2. Ядром 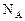 линейного оператора А называется множество всех векторов
линейного оператора А называется множество всех векторов 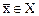 , для которых
, для которых 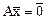 .
.
Ядро 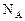 является линейным подпространством пространства Х. Его размерность
является линейным подпространством пространства Х. Его размерность 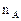 называется дефектом оператора А.
называется дефектом оператора А.
Если оператор А действует в -мерном пространстве Х, то справедливо следующее соотношение 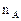 +
+ 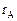 =
= 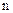 .
.
Оператор А называется невырожденным, если его ядро 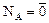 . Ранг невырожденного оператора
. Ранг невырожденного оператора 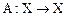 равен размерности пространства Х.
равен размерности пространства Х.
Пусть 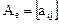 - матрица линейного преобразования А пространства Х в некотором базисе, тогда координаты образа
- матрица линейного преобразования А пространства Х в некотором базисе, тогда координаты образа 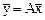 и прообраза
и прообраза 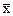 связаны соотношением
связаны соотношением
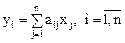 .
.
Поэтому координаты любого вектора 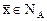 удовлетворяют системе уравнений
удовлетворяют системе уравнений
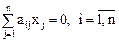 .
.
Отсюда следует, что ядро линейного оператора является линейной оболочкой фундаментальной системы решений данной системы.
Задачи
1. Доказать, что ранг оператора равен рангу его матрицы в произвольном базисе.
Вычислить ядра линейных операторов, заданных в некотором базисе пространства Х следующими матрицами:
2. 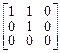 3.
3. 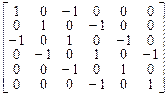
4. 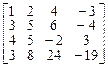
5. Доказать, что 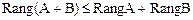 .
.
Вычислить ранг и дефект операторов, заданных следующими матрицами:
6. 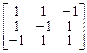 . 7.
. 7. 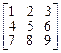 . 8.
. 8. 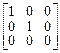 .
.
3. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЛИНЕЙНОГО ОПЕРАТОРА
Рассмотрим линейный оператор А, действующий в 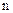 - мерном пространстве Х.
- мерном пространстве Х.
Определение. Число l называется собственным значением оператора А, если 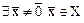 , такой, что
, такой, что 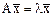 . При этом вектор
. При этом вектор 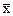 называется собственным вектором оператора А.
называется собственным вектором оператора А.
Важнейшим свойством собственных векторов линейного оператора является то, что собственные векторы, соответствующие попарно различным собственным значениям линейно независимы.
Если 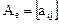 - матрица линейного оператора А в базисе
- матрица линейного оператора А в базисе 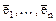 пространства Х, то собственные значения l и собственные векторы
пространства Х, то собственные значения l и собственные векторы 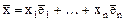 оператора А определяются следующим образом:
оператора А определяются следующим образом:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
1. Собственные значения находят как корни характеристического уравнения (алгебраического уравнения 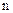 -ой степени):
-ой степени):
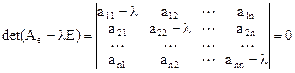 .
.
2. Координаты всех 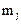 линейно независимых собственных векторов
линейно независимых собственных векторов 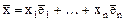 , соответствующих каждому отдельному собственному значению
, соответствующих каждому отдельному собственному значению 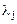 , получают, решая систему
, получают, решая систему 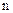 однородных линейных уравнений:
однородных линейных уравнений:
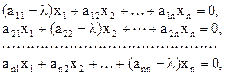
матрица которой имеет ранг 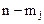 . Фундаментальные решения этой системы являются вектор – столбцами из координат собственных векторов.
. Фундаментальные решения этой системы являются вектор – столбцами из координат собственных векторов.
Корни характеристического уравнения 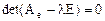 называют также собственными значениями матрицы
называют также собственными значениями матрицы 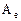 , а решения системы
, а решения системы 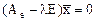 - собственными векторами матрицы
- собственными векторами матрицы 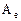 .
.
Пример. Найти собственныевекторы и собственные значения оператора А, заданного в некотором базисе матрицей
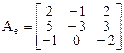
1. Для определения собственных значений составляем и решаем характеристическое уравнение 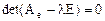 :
:
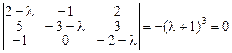 .
.
Отсюда собственное значение 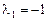 , его кратность
, его кратность 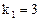 .
.
2. Для определения собственных векторов составляем и решаем систему уравнений 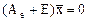 :
:
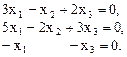
Эквивалентная система базисных уравнений имеет вид
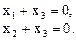
Поэтому всякий собственный вектор представляет собой вектор-столбец 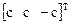 , где с – произвольная константа.
, где с – произвольная константа.
3.1.Оператор простой структуры.
Определение. Линейный оператор А, действующий в n – мерном пространстве называется оператором простой структуры, если ему соответствует ровно n линейно независимых собственных векторов. В этом случае можно построить базис пространства из собственных векторов оператора, в котором матрица оператора имеет наиболее простой диагональный вид
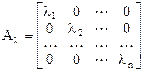 ,
,
где 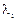 - собственные значения оператора. Очевидно, что верно и обратное: если в некотором базисе пространства Х матрица оператора имеет диагональный вид, то базис состоит из собственных векторов оператора.
- собственные значения оператора. Очевидно, что верно и обратное: если в некотором базисе пространства Х матрица оператора имеет диагональный вид, то базис состоит из собственных векторов оператора.
Линейный оператор А является оператором простой структуры тогда и только тогда, когда каждому собственному значению 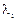 кратности
кратности 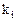 соответствует ровно
соответствует ровно 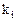 линейно независимых собственных векторов. Так как собственные векторы есть решения системы уравнений
линейно независимых собственных векторов. Так как собственные векторы есть решения системы уравнений 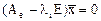 то, следовательно, каждому корню
то, следовательно, каждому корню 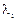 характеристического уравнения
характеристического уравнения 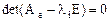 кратности
кратности 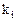 , должна соответствовать матрица
, должна соответствовать матрица 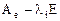 ранга
ранга 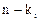 .
.
Всякая матрица 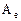 размера
размера 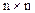 , соответствующая оператору простой структуры, подобна диагональной матрице
, соответствующая оператору простой структуры, подобна диагональной матрице 
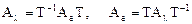 ,
,
где матрица перехода Т от исходного базиса к базису из собственных векторов имеет своими столбцами вектор-столбцы из координат собственных векторов матрицы 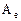 (оператора А).
(оператора А).
Пример. Привести матрицу линейного оператора к диагональному виду
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
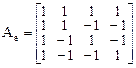 .
.
Составим характеристическое уравнение и найдем его корни.
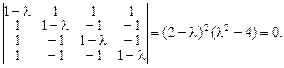
Откуда собственные значения 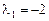 кратности
кратности 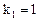 и
и 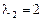 кратности
кратности 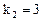 .
.
Первое собственное значение 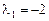 . Ему соответствуют собственные векторы, координаты которых являются
. Ему соответствуют собственные векторы, координаты которых являются
решением системы
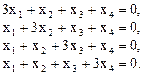
Ранг данной системы равен 3, поэтому имеется только одно независимое решение, например, вектор 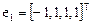 .
.
Собственные векторы, соответствующие 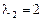 , определяются системой уравнений
, определяются системой уравнений
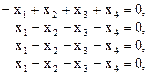
ранг которой равен 1 и, следовательно, существует три линейно независимых решения, например,
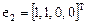 ,
, 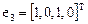 ,
, 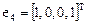 .
.
Таким образом, каждому собственному значению 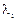 кратности
кратности 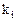 соответствует ровно
соответствует ровно 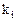 линейно независимых собственных векторов и, следовательно, оператор является оператором простой структуры. Матрица перехода Т имеет вид
линейно независимых собственных векторов и, следовательно, оператор является оператором простой структуры. Матрица перехода Т имеет вид
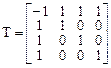
и связь между подобными матрицами  и
и  определяется соотношением
определяется соотношением
 =
= 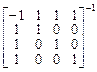
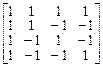
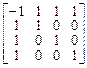 .
.
Задачи
Найти собственные векторы и собственные значения
линейных операторов, заданных в некотором базисе матрицами:
1. 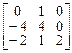 2.
2. 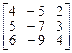 3.
3. 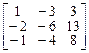
4.  5.
5.  6.
6. 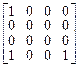
Определить какие из следующих линейных операторов можно привести к диагональному виду путем перехода к новому базису. Найти этот базис и соответствующую ему матрицу:
7. 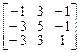 8.
8. 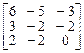 9.
9. 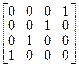
10. Доказать, что собственные векторы линейного оператора, соответствующие различным собственным значениям линейно независимы.
11. Доказать, что если линейный оператор А, действующий в 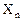 , имеет n различных значений, то любой линейный оператор В перестановочный с А, обладает базисом собственных векторов, причем любой собственный вектор А будет собственным и для В.
, имеет n различных значений, то любой линейный оператор В перестановочный с А, обладает базисом собственных векторов, причем любой собственный вектор А будет собственным и для В.
ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА
Определение 1.. Подпространство L линейного пространства X называется инвариантным относительно оператора А, действующего в X, если для каждого вектора 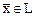 его образ
его образ 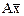 также принадлежит
также принадлежит 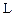 .
.
Основные свойства инвариантных подпространств определяются следующими соотношениями:
1. Если 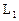 и
и 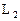 являются инвариантными подпространствами относительно оператора А, то их сумма
являются инвариантными подпространствами относительно оператора А, то их сумма 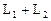 и пересечение
и пересечение 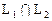 также инвариантны относительно оператора А.
также инвариантны относительно оператора А.
2. Если пространство Х разлагается в прямую сумму подпространств 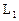 и
и 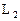 (
(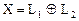 ) и
) и 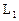 инвариантно относительно А, то матрица оператора в базисе, который является объединением базисов
инвариантно относительно А, то матрица оператора в базисе, который является объединением базисов 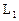 и
и 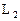 есть блочная матрица
есть блочная матрица
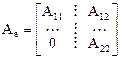 ,
,
где 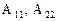 - квадратные матрицы, 0 – нулевая матрица.
- квадратные матрицы, 0 – нулевая матрица.
3. Во всяком инвариантном относительно оператора А подпространстве оператор имеет хотя бы один собственный вектор.
Пример 1. Рассмотрим ядро 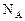 некоторого оператора А, действующего в Х. По определению
некоторого оператора А, действующего в Х. По определению 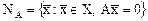 . Пусть
. Пусть 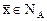 . Тогда
. Тогда 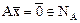 , так как нулевой вектор содержится во всяком линейном подпространстве. Следовательно, ядро
, так как нулевой вектор содержится во всяком линейном подпространстве. Следовательно, ядро 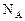 - инвариантное относительно А подпространство.
- инвариантное относительно А подпространство.
Пример 2. Пусть в некотором базисе пространства Х оператор А задается матрицей
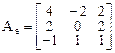 .
.
Определить все подпространства трехмерного пространства, инвариантные относительно А.
Проще всего задача решается в базисе, составленном из собственных векторов оператора, если такой базис существует. Поэтому найдем вначале собственные векторы А.
Составим и решим характеристическое уравнение
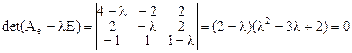 .
.
Откуда собственные значения 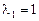 кратности
кратности 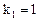 и
и 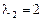 кратности
кратности 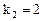 . Первое собственное значение простое. Соответствующий ему собственный вектор определяется системой уравнений
. Первое собственное значение простое. Соответствующий ему собственный вектор определяется системой уравнений
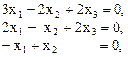
решая которую получим, например, 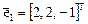 .
.
Собственные векторы для 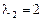 определяются уравнением
определяются уравнением
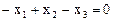 ,
,
имеющим два линейно независимых решения, например, 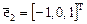 и
и 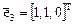 . Таким образом, в нашем случае существует базис из собственных векторов.
. Таким образом, в нашем случае существует базис из собственных векторов.
Пусть теперь 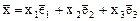 . Тогда вектор
. Тогда вектор 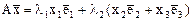 . Воспользовавшись теперь определением инвариантного подпространства, получим, что инвариантными будут следующие подпространства:
. Воспользовавшись теперь определением инвариантного подпространства, получим, что инвариантными будут следующие подпространства:
1. Прямая с базисным вектором 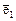 .
.
2. Прямые с базисными векторами 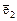 и
и 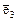 .
.
3. Линейная оболочка векторов 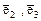 , т.е. плоскость, задаваемая уравнением
, т.е. плоскость, задаваемая уравнением 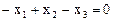 .
.
4. Линейные оболочки векторов 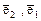 и
и 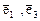 .
.
5. Все трехмерное пространство и нулевое пространство.
Задачи
1. Линейный оператор А задается в базисе 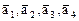
матрицей
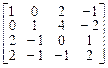 .
.
Показать, что линейная оболочка векторов 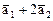 и
и 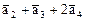 является подпространством инвариантным относительно оператора А.
является подпространством инвариантным относительно оператора А.
2. Доказать, что линейная оболочка любой системы собственных векторов оператора А является инвариантным подпространством.
3. Найти все подпространства трехмерного пространства, инвариантные относительно оператора, заданного в некотором базисе матрицей
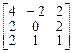 .
.
4. Найти все подпространства трехмерного пространства, инвариантные относительно двух линейных операторов, заданных матрицами
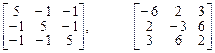 .
.
5. Доказать, что любое подпространство 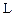 , инвариантное относительно невырожденного оператора А, будет инвариантно и относительно обратного оператора
, инвариантное относительно невырожденного оператора А, будет инвариантно и относительно обратного оператора 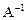 .
.
6. Пусть линейное преобразование А 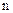 -мерного пространства
-мерного пространства 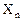 в базисе
в базисе 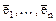 имеет диагональную матрицу с различными элементами на диагонали. Найти все подпространства, инвариантные относительно А, и определить их число.
имеет диагональную матрицу с различными элементами на диагонали. Найти все подпространства, инвариантные относительно А, и определить их число.
|
|
