Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Матрица линейного оператора.

Рассмотрим линейный оператор A: C®C (линейное преобразование пространства C). Пусть векторы 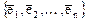образуют базис пространства C. Подействуем оператором А на базисные векторы. В результате получим векторы 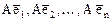. Так как вектор 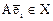, то его можно разложить по базису:

.

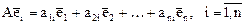В результате получаем матрицу:

,

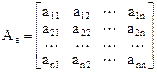i- ый столбец которой есть вектор-столбец из координат вектора 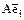в базисе 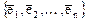. Матрица 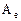называется матрицей линейного оператора 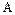в заданном базисе .

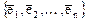Пусть теперь 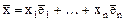- произвольный вектор из C, а 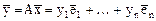- его образ при линейном преобразовании А. Тогда координаты векторов 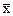и 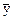связаны соотношением:

.

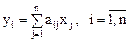Таким образом, действие линейного оператора на вектор сводится к преобразованию его координат с помощью матрицы линейного оператора. Задание матрицы линейного оператора является наиболее удобным способом определения оператора действующего в конечномерном пространстве.

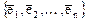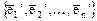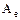Пусть С- матрица перехода от базиса к базису , а и 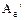- матрицы оператора в первом и втором базисе соответственно. Тогда имеют место соотношения:

.

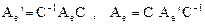Матрицы 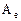и 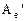, связанные между собой данными соотношениями, называются подобными матрицами.

Действиям над линейными операторами соответствуют точно такие же действия над их матрицами. Если А и В линейные операторы, действующие в Х и 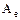, 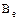- матрицы этих операторов в одном и том же базисе, то:

1. Оператору А+В соответствует матрица .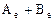

2. Оператору 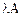соответствует матрица .

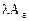3. Оператору АВ соответствует матрица .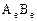

4.Если оператор В=А^-1 , то матрица .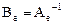

Пример 1. Вычислим матрицу тождественного оператора Е. По определению 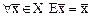. Пусть 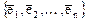базис в Х. Тогда вектор 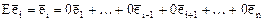. Поэтому тождественному оператору соответствует единичная матрица:

.

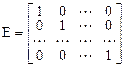Пример 2. Покажем, что поворот плоскости на угол a вокруг начала координат является линейным преобразованием, и найдем матрицу этого преобразования в любом ортонормированном базисе. Предполагается, что положительное направление отсчета углов совпадает с направлением кратчайшего поворота, переводящего базисный вектор 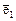во второй вектор базиса 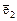. Покажем, во-первых, что данный оператор является линейным. Пусть 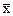- радиус-вектор произвольной точки плоскости. Обозначим его координаты 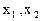, модуль через r, угол с базисным вектором 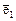через j. Тогда

.

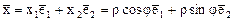Образ вектора 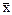вектор 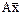будет равен

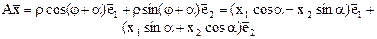
Рассмотрим теперь сумму двух векторов

.

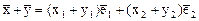Тогда образ суммы

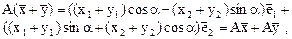
т. е. выполняется свойство аддитивности линейного оператора. Аналогично можно проверить выполнение свойства однородности 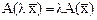. Найдем теперь матрицу оператора в базисе 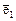, 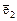. Так как базис ортонормированный, то 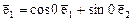и 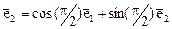. Тогда образы базисных векторов равны 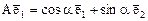и 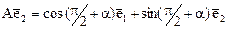. Откуда матрица оператора имеет вид

.

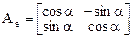Пример 3. Линейный оператор А в базисе , , ,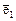

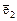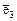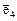
имеет матрицу

.

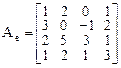Необходимо найти матрицу этого оператора в базисе , , , .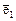

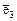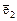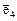Векторы двух базисов «старого» 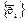и «нового» 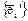связаны соотношениями 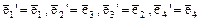. Поэтому матрица перехода С от базиса 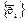к базису 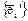имеет вид:

.

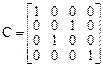Тогда матрица оператора А в «новом» базисе

.

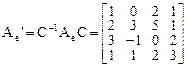Задачи

1. Пусть А и В- линейные операторы, действующие из Х в U. Показать, что оператор С=А+В является линейным.

2. Показать, что сложение операторов обладает следующими свойствами:

А+В=В+А,

(А+В)+С=А+(В+С).

3. Пусть А и В- линейные операторы. Показать, что оператор С=АВ является линейным.

4. Выяснить, какие из следующих операторов А, определенных путем задания координат вектора 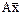как функций координат вектора 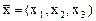, являются линейными, и найти их матрицы в том же базисе, в котором заданы координаты вектора :

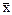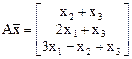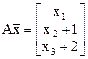а) b) с)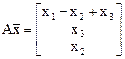

5. Доказать, что существует единственное линейное преобразование трехмерного пространства, переводящее векторы 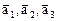соответственно в 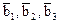и найти матрицу этого преобразования в том же базисе, в котором заданы координаты всех векторов:

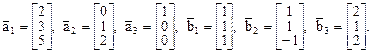
6. Линейное преобразование j в базисе 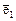, , 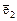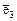имеет матрицу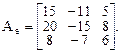

Найти его матрицу в базисе , , .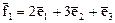

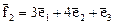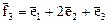7. Пусть оператор А в базисе 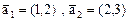имеет матрицу 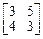, оператор В в базисе 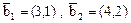имеет матрицу 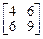. Найти матрицу оператора А+В в базисе .

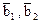8. Доказать, что любое линейное преобразование А одномерного пространства сводится к умножению всех векторов на одно и то же число, т.е. .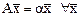

9. Как изменится матрица линейного оператора, если в базисе 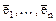поменять местами векторы 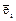и 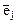?