
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Знакоопределенные и знакопеременные квадратичные формы
|
|
Квадратичные формы подразделяют на типы в зависимости от множества принимаемых ими значений.
Определение 6.11. Квадратичная форма  называется:
называется:
 положительно определенной, если для всякого ненулевого вектора
положительно определенной, если для всякого ненулевого вектора 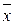 :
: 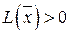 ;
;
 отрицательно определенной, если для всякого ненулевого вектора
отрицательно определенной, если для всякого ненулевого вектора 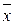 :
: 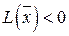 ;
;
 неположительно определенной (отрицательно полуопределенной), если для всякого ненулевого вектора
неположительно определенной (отрицательно полуопределенной), если для всякого ненулевого вектора 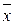 :
: 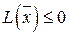 ;
;
 неотрицательно определенной (положительно полуопределенной), если для всякого ненулевого вектора
неотрицательно определенной (положительно полуопределенной), если для всякого ненулевого вектора 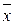 :
:  ;
;
 знакопеременной, если существуют ненулевые векторы
знакопеременной, если существуют ненулевые векторы 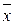 ,
, 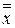 :
:  .
.
Определение 6.12. Положительно (отрицательно) определенные квадратичные формы называются знакоопределенными. Неположительно (неотрицательно) определенные квадратичные формы называются знакопостоянными.
Тип квадратичной формы можно легко определить, приведя ее к каноническому (или нормальному) виду. Справедливы следующие две теоремы.
Теорема 6.6. Пусть квадратичная форма  приведена к каноническому виду и имеет сигнатуру
приведена к каноническому виду и имеет сигнатуру  (
( ,
, 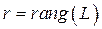 ). Тогда:
). Тогда:

 является положительно определенной
является положительно определенной 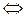
 ;
;

 является отрицательно определенной
является отрицательно определенной 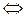
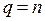 ;
;

 является неположительно определенной
является неположительно определенной 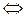
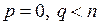 ;
;

 является неотрицательно определенной
является неотрицательно определенной 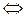
 ;
;

 является знакопеременной
является знакопеременной 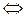
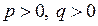 .
.
Из теоремы в частности следует, что всякая знакоопределенная форма является невырожденной ( ,
, 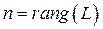 ), всякая знакопостоянная форма является вырожденной (
), всякая знакопостоянная форма является вырожденной ( ,
, 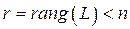 ). Знакопеременная форма может являться как невырожденной, так и вырожденной.
). Знакопеременная форма может являться как невырожденной, так и вырожденной.
Ниже в таблице указаны примеры квадратичных форм (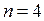 ), записанных в каноническом (или нормальном) виде, их тип и сигнатуры.
), записанных в каноническом (или нормальном) виде, их тип и сигнатуры.
| № | Квадратичная форма | Сигнатура | Тип формы |

| 
| Положительно определенная | |
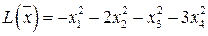
| 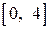
| Отрицательно определенная | |
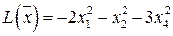
| 
| Неположительно определенная | |
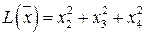
| 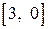
| Неотрицательно определенная | |
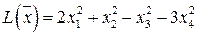
| 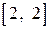
| Знакопеременная, невырожденная | |
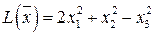
| 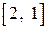
| Знакопеременная, вырожденная |
Теорема 6.7. Пусть квадратичная форма  приведена к каноническому виду
приведена к каноническому виду 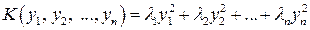 методом ортогональных преобразований (
методом ортогональных преобразований (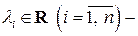 собственные значения матрицы формы
собственные значения матрицы формы  ). Тогда:
). Тогда:

 является положительно определенной
является положительно определенной 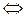 при всех
при всех 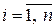
 ;
;

 является отрицательно определенной
является отрицательно определенной 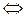 при всех
при всех 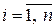
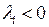 ;
;

 является неположительно определенной
является неположительно определенной 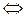 при всех
при всех 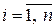
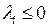 ;
;
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение

 является неотрицательно определенной
является неотрицательно определенной 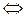 при всех
при всех 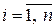
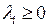 ;
;

 является знакопеременной
является знакопеременной 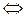 среди собственных чисел есть как положительные, так и отрицательные.
среди собственных чисел есть как положительные, так и отрицательные.
|
|
