Нормальный вид квадратичной формы

Согласно теореме Лагранжа любую квадратичную форму можно привести к каноническому виду. То есть существует диагонализирующий (канонический) базис, в котором матрица этой квадратичной формы имеет диагональный вид

,

где . Тогда в этом базисе квадратичная форма имеет вид

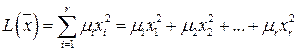. (6.17)

Пусть среди ненулевых элементов имеется 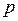положительных и отрицательных, причем . Меняя, в случае необходимости нумерацию базисных векторов, можно всегда добиться того, чтобы в диагональной матрице квадратичной формы первые 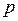элементов были положительными, остальные – отрицательными (если 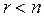, то последние элементов в матрице – нули). В результате квадратичную форму (6.17) можно записать в следующем виде

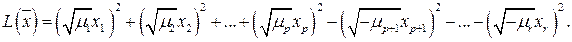(6.18)

В результате замены переменных 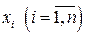на переменные согласно системе:

квадратичная форма (6.18) примет диагональный вид, в которой коэффициенты при квадратах переменных единицы, минус единицы или нули:

, (6.19)

где матрица квадратичной формы (6.19) имеет диагональный вид

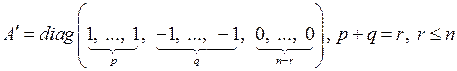. (6.20)

Определение 6.9. Запись (6.19) называется нормальным видом квадратичной формы, а диагонализирующий базис, в котором квадратичная форма имеет матрицу (6.20), называется нормализирующим базисом.

Таким образом, в нормальном виде (6.19) квадратичной формы диагональными элементами матрицы (6.20) могут быть единицы, минус единицы или нули, причем располагаются они так, что сначала первыми идут 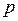единиц, затем минус единиц, потом 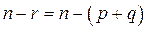нулей (не исключаются случаи обращения в нуль указанных значений , , ).

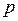Таким образом, доказана следующая теорема.

Теорема 6.3. Всякая квадратичная форма может быть приведена к нормальному виду (6.19) с диагональной матрицей (6.20).