Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Диапазон чисел, потеря значимости, переполнение

Рассмотренные принципы представления чисел с ПЗ поясним на примере. На рис. 2.21 представлен типичный 32-битовый формат числа с ПЗ.

Рисунок -Типичный 32-битовый формат числа с плавающей запятой

Старший (левый) бит содержит знак числа.

Значение смещенного порядка хранится в разрядах с1-го по 8-й и может находиться в диапазоне от 0 до 255: Для получения фактического значения порядка из содержимого этого поля нужно вычесть фиксированное значение, равное 128. С таким смещением фактические значения порядка могут лежать в диапазоне от -128 до +127. В примере предполагается, что основание системы счисления равно 2.

Третье поле слова содержит нормализованную мантиссу со скрытым разрядом (единицей). Благодаря такому приему 23-разрядное поле позволяет хранить 24-разрядную мантиссу в диапазоне от 0, 5 до 1, 0.

На рис. 2.22 приведены диапазоны чисел, которые могут быть записаны с помощью 32-разрядного слова.

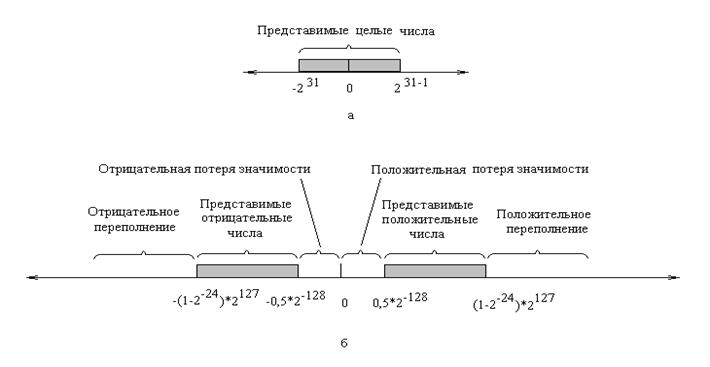
Рисунок -Числа представимые в 32-битовых форматах: а – целые числа с фиксированной запятой; б – числа с плавающей запятой

В варианте с ФЗ для целых чисел в дополнительном коде могут быть представлены все целые числа от -2 ³¹ до 2 ³¹-1, то есть 2 ³² различных чисел (см. рис. 2.22, а).

Для случая ПЗ возможны следующие диапазоны чисел (см. рис. 2.22, б)

- отрицательные числа между –(1-2^-24)*2¹²⁷ и -0, 5*2^-128;

- положительные числа между 0, 5*2^-128 и (1-2^-24)*2¹²⁷;

В эту область не включены четыре участка:

- отрицательные числа, меньшие чем –(1-2^-24)*2¹²⁷ – отрицательное переполнение;

- отрицательные числа, большие чем -0, 5 * 2 ¹²⁸ — отрицательная потеря значимости;

- положительные числа, меньшие, чем 0, 5 * 2^-28 — положительная потеря значимости;

- положительные числа, большие чем (1 – 2^-24) * 2¹²⁷ — положительное переполнение.

Показанная запись числа с ПЗ не учитывает нулевого значения. Для этой цели используется специальная кодовая комбинация.

Переполнения возникают, когда в результате арифметической операции получается значение большее, чем можно представить порядком 127 (2¹²⁰ х 2¹⁰⁰ = 2²³⁰).

Потеря значимости — это когда результат представляет собой слишком маленькое дробное значение (2^-120 х 2^-100 = 2^-230). Потеря значимости является менее серьезной проблемой, поскольку такой результат обычно рассматривают как нулевой.

Для формата, изображенного на рис. 2.21, имеет место противоречие между диапазоном и точностью. Если увеличить число битов, отведенных под порядок, расширяется диапазон представимых чисел. Однако, поскольку может быть представлено только фиксированное число различных значений, уменьшается плотность и тем самым точность. Единственный путь увеличения, как диапазона, так и точности, это увеличение количества разрядов, поэтому в большинстве ВМ предлагается использовать числа в одинарном и двойном форматах. Например, число одинарного формата может занимать 32 бита, а двойного — 64 бита.