💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Граф G7

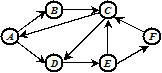
Длина пути во взвешенном графе равна сумме весов дуг, входящих в этот путь.

Путь, не содержащий одинаковых узлов (за исключением, может быть, n ₀= n _k), называется простым.

Путь от узла к самому себе, не содержащий одинаковых дуг, называется циклом. Если граф содержит цикл, то он называется циклическим, в противном случае – ациклическим.

Расстояние между двумя узлами – это длина кратчайшего пути, соединяющего эти узлы.

Граф называется связным, если для любой пары узлов существует соединяющий их путь. Например, граф G 3 связный, а графы G 4 – G 6 – нет. Очевидно, что ориентированный граф не будет связным, если в нем есть узлы, не имеющие входящих или исходящих дуг. Неориентированный граф несвязный, если он содержит узлы, не имеющие инцидентных с ним дуг.

Связный ориентированный граф без петель называется сетью.

2. Операции над графом

Над графом g могут быть выполнены следующие операции:

– возвращение адреса узла со значением v – NodeAddr (g, v);

– проверка смежности узлов Node1 и Node 2 – ArcAddr (g, Node1, Node2);

– возвращение начального узла дуги Arc – HeadNode (g, Arc);

– возвращение конечного узла дуги Arc – RearNode (g, Arc);

– возвращение информации, содержащейся в узле, – Value (g, Node);

– проверка наличия узлов в графе – Empty (g);

– включение дуги между узлами Node1 и Node2 – AddArc (g, Node1, Node2);

– исключение дуги между узлами Node1 и Node2 – DeleteArc (g, Node1, Node2);

– включение узла со значением v в граф – AddNode (g, v);

– исключение из графа узла Node с исключением инцидентных ему дуг и возвращение значения информационного поля узла – DeleteNode (g, Node);

– определение количества узлов в графе – NodesQuantity (g);

– просмотр графа – Revision (g);

– создание пустого графа – Create (g);

– удаление всех узлов и дуг графа – Clear (g);

– построение графа – Build (g).

С использованием вышеперечисленных операций можно реализовать более сложные операции: определение расстояния (кратчайшего пути) между двумя заданными узлами графа; поиск узлов в графе; определение путей между двумя заданными узлами графа и их длин и др.

Графы применяют для решения задач планирования и распределения работ проекта, транспортных задач, задач о потоках в сетях и других.

3. Реализация графа

Одним из способов представления графа является матричный способ. При представлении графа с помощью матрицы инцидентности строки матрицы соответствуют узлам графа, а столбцы – дугам; на пересечении каждой строки и столбца ставится 1, если дуга инцидентна узлу, и 0 в противном случае.

Граф представляют также с помощью матрицы смежности узлов. И строки и столбцы матрицы при этом соответствуют узлам графа, а на пересечении каждой строки и столбца ставится 1, если соответствующие узлы смежные, и 0 в противном случае.

Несмотря на очевидные преимущества (простота включения и исключения дуг, простота реализации большинства основных алгоритмов обработки графа), матричное представление графа не всегда удобно, поскольку число узлов (и дуг для матрицы инцидентности) требуется знать заранее. Если граф должен создаваться или изменяться во время выполнения программы, то для каждого добавления или удаления узла надо строить новую матрицу. Кроме того, память должна быть отведена для всех возможных дуг.

Очевидным решением является представление графа, при котором все узлы графа и инцидентные им дуги объединены в связанные списки. Конкретные реализации списковых структур могут быть различными: односвязные и двусвязные, линейные и циклические списки.

Списковое представление является одним из наиболее удобных и универсальных способов представления графа и позволяет представлять любые графы: ориентированные и неориентированные, взвешенные и невзвешенные, хранить информацию, связанную с дугами и узлами графа.

Рассмотрим один из способов связанного представления графа. Узлы графа объединяются в список, каждый элемент которого содержит три поля: Value (информация, связанная с узлом графа), NextNode (указатель на следующий элемент списка узлов графа) и ArcList (указатель на список дуг, выходящих из данного узла, – список смежности). Каждый элемент списка смежности представляет дугу графа и содержит два поля: RearNode (указатель на элемент в списке узлов графа, которым заканчивается дуга) и NextArc (указатель на следующий элемент списка смежности данного узла). Для взвешенного графа элемент списка дуг должен содержать дополнительное поле Weight (вес дуги). Для неориентированного графа список дуг для каждого узла должен содержать все дуги, инцидентные этому узлу (входящие и выходящие), при этом каждая дуга будет присутствовать в представлении графа дважды, так как инцидентна двум узлам.

Пример ориентированного невзвешенного графа и его представление с помощью линейных односвязных списков:

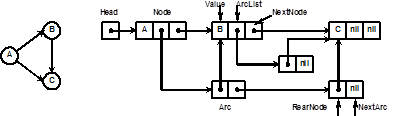
Переменная ссылочного типа Head указывает на начало списка узлов графа. Каждый узел Node графа состоит из трех полей: Value, ArcList и NextNode. Дуга Arc содержит два поля: NextArc и RearNode. Последний узел графа и последняя дуга из списка дуг каждого узла содержат указатель nil. Поле ArcList узла содержит значение nil в том случае, если этот узел не имеет исходящих из него дуг.

Описание класса tOrGraph (Oriented Graph – ориентированный граф) с использованием линейных односвязных списков имеет вид:

Type

tValue = Char; // тип информационной части узла графа – Char

pArc = ^tArc; // тип указателя на дугу графа

pNode = ^tNode; // тип указателя на узел графа

tNode = record // тип узла графа

Value: tValue; // информационная часть узла графа

NextNode: pNode; // указатель на следующий узел графа

ArcList: pArc; // указатель на список смежности узла

end; // tNode

tArc = record // тип элемента списка смежности узла - дуги графа

RearNode: pNode; // указатель на узел, являющийся концом дуги

NextArc: pArc; // указатель на следующую дугу узла графа

end; // tArc

tOrGraph= class // класс – ориентированный граф