While not Eof(f) do begin

Read(f, Key); if Eoln(f) then ReadLn(f);

Search(Key); // функция Search вызывается как процедура

end;

end; //procedure tSearchTree.Build

11. Сбалансированные деревья

Поиск по дереву является эффективным только в том случае, если дерево будет идеально сбалансированным, так как среднее число сравнений, необходимых для обнаружения ключа, в идеально сбалансированном дереве равно log₂ n. Если дерево вырождается в список, то эта величина примерно равна n /2. Анализ показывает, что процедура балансировки, восстанавливающая после каждого случайного включения идеально сбалансированное дерево, не всегда является выгодной, так как реализуется довольно сложно.

Возможным выходом из положения является введение менее строгого понятия сбалансированности. Это может привести к более простой процедуре балансировки за счет незначительного увеличения времени поиска. Одно из таких определений сбалансированного дерева было предложено Г.М. Адельсон-Вельским и Е.М. Ландисом. Их критерий сбалансированности сформулирован следующим образом.

Дерево называется сбалансированным, если высоты двух поддеревьев каждого из его узлов отличаются не более чем на единицу.

Деревья, удовлетворяющие такому условию, часто называют АВЛ-деревьями (по имени их открывателей). Мы их будем называть сбалансированными деревьями. В таких деревьях, как доказали их авторы, операция поиска выполняется за время, пропорциональное log₂ n.

12. Включение в сбалансированное дерево

Есть корень r, левое (L) и правое (R) поддеревья с высотами h_L и h_R соответственно. Что может произойти при включении в сбалансированное дерево нового узла?

Предположим, включение в L нового узла приведет к увеличению на 1 его высоты; тогда возможны три ситуации:

1) h_L = h_R: после включения L и R станут разной высоты, но критерий сбалансированности не будет нарушен;

2) h_L < h_R: после включения L и R станут равной высоты, т.е. сбалансированность улучшится;

3) h_L > h_R: после включения критерий сбалансированности нарушится и дерево необходимо перестраивать.

Например, в сбалансированное дерево, приведенное ниже, узлы с ключами 9 и 11 можно включить, не нарушая его сбалансированности. Включение узлов 1, 3, 5 или 7 потребует последующей балансировки.

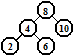
Существуют лишь 2 различные возможности устранения несбалансированности, возникшей из-за включения, требующие индивидуального подхода (оставшиеся могут быть выведены из них на основе симметрии). Эти случаи показаны ниже. Прямоугольниками обозначены поддеревья, причем «добавленная» при включении высота заштрихована.

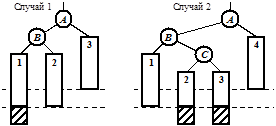
Первый случай возникает, когда в дерево на числовом примере включаются узлы с ключами 1 или 3. Ситуация, характерная для второго случая, возникает при включении узлов с ключами 5 или 7. Простые преобразования восстанавливают желанную сбалансированность. Заметим, что допускаются лишь вертикальные перемещения, относительное горизонтальное расположение узлов и поддеревьев должно оставаться без изменения. Результат балансировки показан ниже.

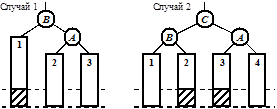
Алгоритм включения и балансировки существенно зависит от того, каким образом хранится информация о сбалансированности дерева. Удобно хранить в каждом узле показатель сбалансированности как разность между высотами правого и левого поддеревьев этого узла:

Type

TBalance= -1..+1; // тип показателя сбалансированности

tItem = record // тип элемента дерева

Value: tValue; // содержательная часть элемента дерева

Left, Right: pItem; // указатели на левое и правое поддеревья

Bal: TBalance; // показатель сбалансированности - разность между

// высотами правого и левого поддеревьев узла

end; // tItem

Процесс включения узла в сбалансированное дерево состоит из трех последовательно выполняемых частей.

1. Проход по пути поиска, пока не убедимся, что ключа нет.

2. Включение нового узла и определение результирующего показателя сбалансированности.

3. «Отступления» по пути поиска и проверка в каждом узле показателя сбалансированности. Если необходимо – балансировка.

Хотя при таком методе и требуются некоторые избыточные проверки (если сбалансированность уже зафиксирована, то нет необходимости проверять её в вышестоящих узлах), мы воспользуемся этой схемой, так как её можно реализовать расширением функции поиска с включением.

Дополнительная информация, которую нужно передавать на каждом шаге, – изменение высоты поддерева в том месте, где произошло включение. Её можно передавать в виде булевской переменной H, означающей «высота дерева увеличилась».

Рассмотрим процесс возвращения к узлу Item после включения в его левое поддерево, причем известно, что высота Item увеличилась.

В зависимости от высоты поддеревьев перед включением мы должны различать три возможные ситуации:

1) h_L < h_R, Item ^. Bal = +1, предыдущая несбалансированность в Item уравновешивается;

2) h_L = h_R, Item^.Bal = 0, левое поддерево стало «перевешивать», но балансировка не нужна;

3) h_L > h_R, Item^.Bal = –1, необходима балансировка;

В третьей ситуации по показателю сбалансированности корня p 1 левого поддерева можно определить, с каким из случаев балансировки мы имеем дело. Если p1^.Bal = –1 (левое поддерево этого узла также выше правого), то имеем дело со случаем 1, иначе – со случаем 2.

Операция балансировки состоит только из последовательных переприсваиваний ссылок. Фактически ссылки циклически меняются местами, что приводит к однократному или двукратному повороту двух или трех участвующих в процессе узлов. Кроме вращения ссылок нужно должным образом поправить и показатели сбалансированности соответствующих узлов.

Случай 1 называется однократным LL -поворотом (в левом дереве выросло левое поддерево):

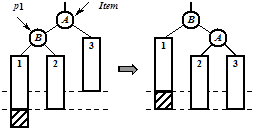
Для реализации LL -поворота необходимо выполнить однократный поворот двух узлов Item и p 1:

Item^.Left: =p1^.Right; p1^.Right: =Item; Item: =p1;

Случай 2 называется двойным LR -поворотом (в левом дереве выросло правое поддерево):

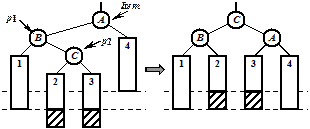
Для реализации LR -поворота необходимо выполнить двукратный поворот трех узлов p1, p2 и Item:

p1^.Right: =p2^.Left; p2^.Left: =p1;

Item^.Left: =p2^.Right; p2^.Right: =Item;

Item: =p2;

Процедура, выполняющая все необходимые действия по балансировке, если высота левого поддерева узла Item увеличилась (Н=True), имеет вид:

procedure LeftBalance(var Item: pItem; var H: Boolean);

// Высота левого поддерева узла Item увеличилась, входное значение Н=True

Var

p1, p2: pItem;

Begin