Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Private

fOperators: tOperatorSet; // поле - множество операторов

Public

function IsOperator(ExprEl: tValue): Boolean; // элемент выражения - оператор?

procedure Build(var f: Text); // построение дерева выражения

constructor Create; // создание пустого дерева

end; // tExprTree

Метод IsOperator проверяет, принадлежит ли очередной элемент выражения к множеству допустимых операторов fOperators. Метод Build дерева выражения перекрывает одноименный метод бинарного дерева, так как реализуется иначе. Конструктор Create помимо создания пустого дерева задает множество Operators разрешенных в данном выражении операторов. Все остальные методы бинарного дерева наследуются.

В простейшем случае – для операндов и операторов, представляемых одним символом, – процедура построения дерева выражения по его префиксной записи, хранящейся в текстовом файле, имеет вид:

procedure TExprTree.Build(var f: Text);

// Построение дерева выражения по его префиксной записи в файле f

function BuildTree: pItem; // рекурсивная функция построения

Var

Item: pItem; // элемент дерева выражения

Symbol: tValue; // символ выражения

Begin

if not Eof(f)

Then begin

Read(f, Symbol); if Eoln(f) then ReadLn(f);

Item: = New(pItem); Item^.Value: = Symbol;

if IsOperator(Symbol)

then begin // cимвол - оператор

Item^.Left: = BuildTree; Item^.Right: = BuildTree; end

else begin // cимвол - операнд

Item^.Left: = Nil; Item^.Right: = nil;

end;

BuildTree: = Item;

end;

end; // function BuildTree

Begin

fRoot: = BuildTree;

end; // procedure TExprTree.Build

7. Дерево поиска

Бинарные деревья часто используются для представления множества данных, среди которых идет поиск элементов по уникальному ключу. Если дерево организовано так, что для каждого узла t все ключи его левого поддерева меньше ключа t, а все ключи правого поддерева t больше ключа t, то такое дерево будем называть деревом поиска. В нем легко найти элемент с нужным ключом – достаточно, начав с корня, двигаться в левое или правое поддерево на основании сравнения заданного ключа с ключом текущего узла. Известно, что из n элементов можно построить бинарное дерево с высотой не более log₂ n, поэтому, если дерево идеально сбалансировано, поиск среди его n элементов выполняется максимум за log₂ n сравнений. Подобные деревья широко используются и для сортировки больших массивов данных, так как обход дерева поиска слева направо дает отсортированную в порядке возрастания последовательность ключей.

При обходе слева направо дерева поиска, приведенного ниже, получается последовательность: 1, 4, 8, 9, 11, 15, 20.

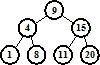
8. Операции над деревом поиска

Над деревом поиска могут быть выполнены все операции, определенные для бинарного дерева. Но в основном к дереву поиска применяются операции, определяемые особенностями его организации:

Ø поиск элемента с заданным ключом Key в дереве и возвращение адреса элемента, если он найден, в противном случае возвращается значение nil – операция Addr(Key);

Ø поиск по дереву с включением – поиск элемента с ключом Key в дереве, подключение узла с этим ключом, если поиск был неудачным, и возвращение адреса элемента с заданным ключом – операция Search(Key);

Ø поиск по дереву с исключением – поиск элемента с заданным ключом в дереве и исключение этого элемента, если он найден, – операция Delete(Key); после исключения дерево должно остаться деревом поиска.

Для построения дерево поиска, можно использовать операцию поиска по дереву с включением Search(Key), считывая из входного потока элементы с заданными ключами и включая их в дерево поиска. Операция Search(Key) может быть построена таким образом, что она будет включать в дерево элемент и в том случае, если он уже существует в дереве. Использование такой операции для построения дерева поиска позволяет построить дерево с повторяющимися ключами.

9. Реализация дерева поиска

В общем случае каждый элемент дерева поиска может содержать в содержательной части Value специальное поле, называемое ключом этого элемента. Для упрощения описания будем считать, что поле Value является ключом элемента дерева. В этом случае класс tSearchTree может быть описан как наследник класса tBinaryTree:

Type

tSearchTree = class (tBinaryTree) // класс - дерево поиска

function Addr(Key: tValue): pItem; // поиск элемента с ключом Key

function Search(Key: tValue): pItem; // поиск с включением

procedure Delete(Key: tValue); // поиск с исключением

procedure Build(var f: Text); // построение дерева поиска

end; // tSearchTree

Метод Build дерева поиска перекрывает одноименный метод бинарного дерева, поскольку реализуется иначе. Поле fRoot и все остальные методы бинарного дерева наследуются деревом поиска. Методы Locate, Search и Delete являются новыми, расширяющими возможности дерева поиска по сравнению с обычным бинарным деревом.

10. Реализация операций над деревом поиска

Поиск элемента с ключом Key может быть выполнен с помощью итерации, так как поиск идет по единственному пути от корня к искомому узлу:

function tSearchTree.Addr(Key: tValue): pItem; // адрес элемента с ключом Key

Var

Item: pItem;

Begin

if Empty

then Addr: = nil