Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Case Item^.Bal of
|
|
+1: begin
// Правое поддерево было выше, увеличение высоты левого
// поддерева не увеличило высоту дерева, балансировка не нужна
H: = False; Item^.Bal: = 0; end;
0: begin
Item^.Bal: = -1; end;
// Поддеревья были одинаковой высоты, увеличение высоты левого
// поддерева увеличило высоту дерева, но балансировка не нужна
-1: begin
// Левое поддерево было выше, увеличение его высоты
// привело к разбалансировке дерева, нужна балансировка:
p1: = Item^.Left;
if p1^.Bal = -1
then begin // однократный LL-поворот
Item^.Left: = p1^.Right; p1^.Right: = Item; Item^.Bal: = 0; Item: = p1; end
else begin // двойной LR-поворот
p2: = p1^.Right; p1^.Right: = p2^.Left; p2^.Left: = p1;
Item^.Left: = p2^.Right; p2^.Right: = Item;
if p2^.Bal = -1 then Item^.Bal: = +1 else Item^.Bal: = 0;
if p2^.Bal = +1 then p1^.Bal: = -1 else p1^.Bal: = 0;
Item: = p2;
end;
// после балансировки показатель сбалансированности равен 0:
Item^.Bal: = 0;
// в результате балансировки высота дерева не увеличилась:
H: = False;
end; // конец балансировки
end; // case
end; // procedure LeftBalance
Мы рассмотрели ситуации, возникающие при включении в левое поддерево узла. При включении в правое поддерево все ситуации будут зеркальным отображением рассмотренных ситуаций. Так, если при включении в правое поддерево выросло его правое поддерево, то получим однократный RR -поворот, если выросло левое поддерево, то двойной RL -поворот. При реализации процедуры RightBalance, работающей, если высота правого поддерева узла Item увеличилась, все левые указатели узлов меняются на правые и наоборот; все показатели сбалансированности узлов также меняются на противоположные (–1 на +1 и наоборот).
Класс tBalanceTree может быть наследником класса tSearchTree с учетом изменения типа tItem элемента дерева:
Type
tValue = Char; // тип элемента дерева - символьный
tBalance = -1..+1; // тип показателя сбалансированности
pItem = ^tItem; // тип - указатель на элемент дерева
tItem = record // тип - элемент дерева
Value: tValue; // содержательная часть элемента дерева
Left, Right: pItem; // указатели на левое и правое поддеревья
Bal: TBalance; // показатель сбалансированности в узле
end; // tItem
// Класс tSearchTree - дерево поиска
tSearchTree = class (tBinaryTree)
function Addr(Key: tValue): pItem; // поиск элемента с ключом Key
function Search(Key: tValue): pItem; virtual; // поиск с включением
procedure Delete(Key: tValue); // поиск с исключением
procedure Build(var f: Text); // построение дерева поиска
end; // tSearchTree
// Класс tBalanceTree - сбалансированное дерево поиска
tBalanceTree = class (tSearchTree)
function Search(Key: tValue): pItem; override; // поиск с включением
// и перебалансировкой
procedure Delete(Key: tValue); // поиск с исключением и перебалансировкой
end; // tBalanceTree
Методы Addr и Build класс tBalanceTree наследует у класса tSearchTree. Методы Search и Delete класса tBalanceTree перекрывают одноименные методы класса tSearchTree, так как реализуются иначе. Метод Search у классов tSearchTree, tBalanceTree должен быть виртуальным, так как наследуемая процедура Build использует его при построении дерева (процедура Build должна вызывать метод Search того класса, для которого она вызывается).
Функция поиска элемента с заданным ключом Key с включением в сбалансированное дерево имеет вид
function TBalanceTree.Search(Key: tValue): pItem;
// поиск элемента с ключом Key с включением в сбалансированное дерево
Var
Addr: pItem; // вспомогательный указатель
H: Boolean; // True, если высота дерева увеличилась
procedure LeftBalance(var Item: pItem; var H: Boolean);
// Высота левого поддерева узла Item увеличилась, входное значение Н=True
… // текст процедуры см. выше
end; // procedure LeftBalance
procedure RightBalance(var Item: pItem; var H: Boolean);
// Высота правого поддерева узла Item увеличилась
…
end; // procedure RightBalance
procedure IncKey(var Item: pItem; var H: Boolean); // рекурсивная процедура включения
Begin
if Item= nil
then begin // элемента с ключом Key нет -> включение
Item: = New(pItem); H: = True;
Item^.Value: = Key; Item^.Bal: = 0;
Item^.Left: = nil; Item^.Right: = nil;
Addr: = Item; Inc(fSize);
End
Else
if Key < Item^.Value
then begin // поиск слева
IncKey(Item^.Left, H);
if H then LeftBalance(Item, H); // выросла левая ветвь
End
Else
if Key > Item^.Value
then begin //поиск справа
IncKey(Item^.Right, H);
if H then RightBalance(Item, H); // выросла правая ветв ь
End
else Addr: = Item; // элемент найден
end; // procedure IncKey
Begin
H: = False;
IncKey(fRoot, H);
Search: = Addr;
end; // function tBalanceTree.Sear ch
При исключении из сбалансированного дерева алгоритм балансировки остается практически тем же, что и при включении, в частности балансировка опять основывается на однократных или двукратных поворотах узлов.
Сложность операции балансировки предполагает, что сбалансированные деревья следует использовать только тогда, когда поиск информации происходит значительно чаще, чем её включение.
Рассмотрим работу процедуры поиска с включением на примере дерева (a). Включение 7 приводит к несбалансированному дереву (b), а его балансировка достигается RR -поворотом (c). Последующее включение узлов с ключами 2 и 1 приводит к несбалансированному дереву (d) с корнем 4, которое балансируется LL -поворотом (e).
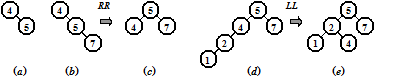
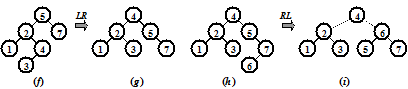
Включение ключа 3 нарушает критерий сбалансированности в узле 5 (f), и балансировка достигается двойным LR -поворотом (g). Включение узла с ключом 6 (h) приводит к четвертому типу балансировки – двойному RL -повороту. Результат – дерево (i).
Лабораторная работа 3.
Бинарные деревья
|
|