
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Координатний простір – Oxyz.
|
|
Якщо взяти три взаємно перпендикулярні координатні прямі – 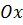 (вісь абсцис),
(вісь абсцис), 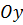 (вісь ординат) та
(вісь ординат) та 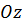 (вісь аплікат), які перетинаються в одній точці
(вісь аплікат), які перетинаються в одній точці 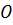 (початок координат), то вони утворять взаємно перпендикулярні координатні площини –
(початок координат), то вони утворять взаємно перпендикулярні координатні площини – 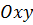 ,
,  ,
, 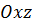 .
.
Осі розбивають координатний простір на 8 частин, які називають октантами.
Точка 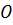 розбиває осі на півосі: додатну і від'ємну.
розбиває осі на півосі: додатну і від'ємну.
Візьмемо довільну точку 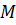 і проведемо через неї площину, паралельну координатній площині
і проведемо через неї площину, паралельну координатній площині  . Вона перетне вісь
. Вона перетне вісь 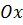 в деякій точці
в деякій точці 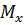 (рис 1).
(рис 1).
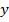
|

|
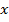
|
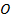
|
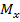
|
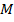
|
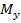
|
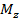
|
| Рис 2 |
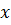 (або абсцисою) точки
(або абсцисою) точки 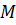 називається число, яке дорівнює за абсолютною величиною довжині відрізка
називається число, яке дорівнює за абсолютною величиною довжині відрізка 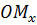 : додатне, якщо точка
: додатне, якщо точка 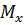 лежить на додатній півосі
лежить на додатній півосі 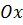 , від'ємне, якщо вона лежить на від'ємній півосі і дорівнює нулю, якщо точка
, від'ємне, якщо вона лежить на від'ємній півосі і дорівнює нулю, якщо точка 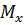 збігається з точкою
збігається з точкою 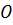 .
.
Проведемо через точку 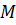 ще дві площини, паралельні відповідно координатним площинам
ще дві площини, паралельні відповідно координатним площинам 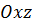 та
та 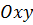 . Вони перетнуть відповідні осі координат
. Вони перетнуть відповідні осі координат 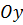 – у точці
– у точці 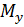 та
та 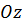 – у точці
– у точці 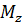 (рис 2).
(рис 2).
Координати точки у просторі позначають так:  , а іноді використовують просто координати, без буквених позначень.
, а іноді використовують просто координати, без буквених позначень.
2 Відстань між точками. Координати середини відрізка.
| xО |
| O |
| A |
| BО |

|
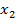
|
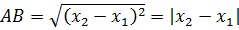
Яка довжина відрізка, зображеного на координатній прямій?
Перевіримо: 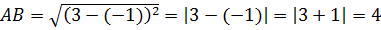
| xО |
| O |
| A |
| BО |
| y |

|
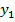
|
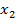
|
|
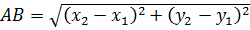
Знайдіть відстань між точками 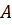 і
і 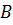 .
.
Перевірте себе: 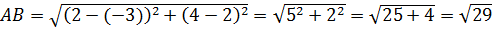
|

|
|
|

|
|
|
|
|
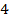
|
Отже, відстань між точками у просторі дорівнюватиме:
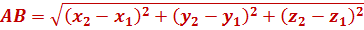
Використовуючи формулу, знайдіть відстань між просторовими точками, зображеними на рисунку.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Перевірте себе: знайдемо координати точок 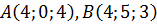
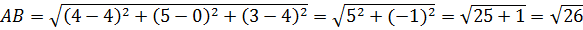
Координати середини відрізка знаходяться як середнє арифметичне координат його кінців. Якщо задано точки 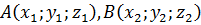 , то координати точки
, то координати точки  дорівнюватимуть:
дорівнюватимуть:
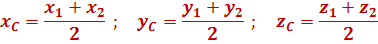
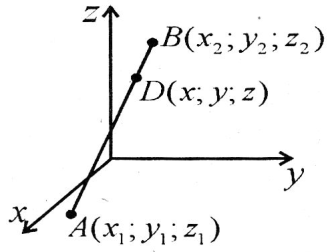
Координати точки, що поділяє відрізок у заданому відношенні теж можна знайти. Якщо відоме відношення відрізків, на які поділено відрізок точкою 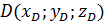 , наприклад,
, наприклад, 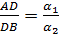 , то координати будуть:
, то координати будуть:

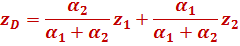
3 Перетворення фігур у просторі.

|
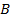
|
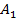
|
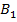
|

|
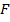
|
 у фігуру
у фігуру 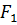 називається рухом, якщо воно зберігає відстані між точками, тобто переводить будь-які дві точки
називається рухом, якщо воно зберігає відстані між точками, тобто переводить будь-які дві точки 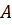 і
і 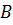 фігури
фігури  в точки
в точки  і
і 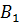 фігури
фігури 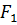 так, що
так, що  .
.
Симетрія відносно площини 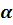 – перетворення фігури
– перетворення фігури  в
в 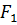 , при якому кожна точка
, при якому кожна точка 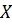 фігури
фігури  переходить в точку
переходить в точку 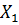 – симетричну до
– симетричну до 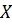 відносно площини
відносно площини  .
.
Нехай  – довільна фіксована площина. З точки
– довільна фіксована площина. З точки 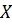 опускають перпендикуляр на площину
опускають перпендикуляр на площину  (точка
(точка 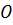 – основа перпендикуляра) і на його продовженні (за точку
– основа перпендикуляра) і на його продовженні (за точку 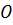 ) відкладають відрізок
) відкладають відрізок 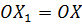 . Точки
. Точки 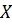 та
та 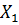 називають симетричними відносно площини
називають симетричними відносно площини  . (рис 1)
. (рис 1)
На рис 2 зображено дві сфери, симетричні відносно площини  .
.
Якщо перетворення симетрії відносно площини переводить фігуру саму в себе, то фігура є симетричною відносно площини  , а площина
, а площина  називається площиною симетрії.
називається площиною симетрії.
На рис 3 зображено площини симетрії сфери. У сфери таких площин симетрій нескінченна множина.
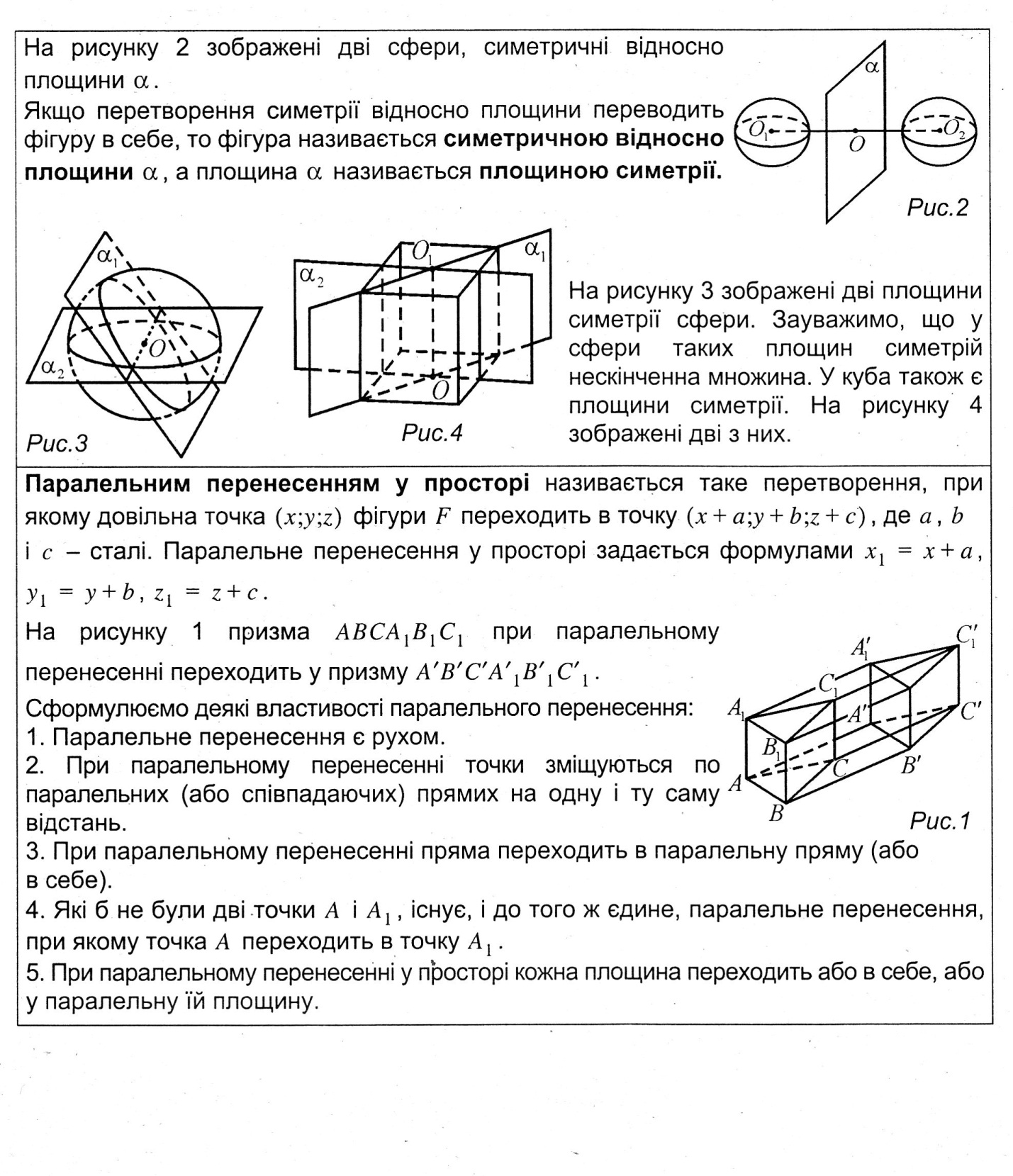

 У куба також є площини симетрії (рис 4), проте їх всього вісім.
У куба також є площини симетрії (рис 4), проте їх всього вісім.

Паралельним перенесенням у просторі називається таке перетворення, при якому довільна точка  фігури
фігури  переходить у точку
переходить у точку 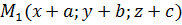 , де
, де 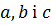 – сталі. Паралельне перенесення у просторі задається формулами:
– сталі. Паралельне перенесення у просторі задається формулами:
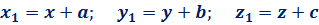 .
.
Властивості паралельного перенесення:
Паралельне перенесення є рухом.
При паралельному перенесенні точки зміщуються по паралельних (або співпадаючих) прямих на одну і ту саму відстань.
При паралельному перенесенні пряма переходить в паралельну пряму (або сама в себе).
Які б не були дві точки, існує, і до того ж єдине, паралельне перенесення, при якому одна точка переходить в іншу.
При паралельному перенесенні у просторі кожна площина переходить або в себе, або у паралельну їй площину.
Гомотетія.
Нехай  – дана фігура і
– дана фігура і 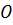 – задана точка. Проведемо через довільну точку
– задана точка. Проведемо через довільну точку 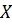 фігури
фігури  промінь
промінь 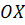 і на ньому відкладемо відрізок
і на ньому відкладемо відрізок 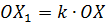 , де
, де 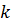 – додатне число.
– додатне число.

 Перетворення фігури
Перетворення фігури  , при якому кожна її точка
, при якому кожна її точка 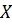 переходить у відповідну їй за побудовою точку
переходить у відповідну їй за побудовою точку 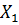 , називається гомотетією відносно центра
, називається гомотетією відносно центра 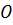 . Число
. Число 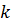 називається коефіцієнтом гомотетії, а фігури
називається коефіцієнтом гомотетії, а фігури  і
і 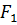 називаються гомотетичними.
називаються гомотетичними.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Перетворення фігури в фігуру називається перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюється (збільшуються або зменшуються) в одне й те саме число разів.
Якщо довільні точки 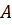 і
і 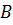 фігури
фігури  при цьому перетворенні переходять в точки
при цьому перетворенні переходять в точки  і
і 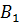 фігури
фігури 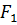 , то
, то  , де
, де 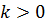 .
.
Число 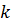 називається коефіцієнтом подібності (
називається коефіцієнтом подібності (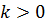 ).
).
При 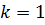 перетворення подібності є рухом.
перетворення подібності є рухом.

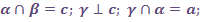
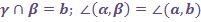
|
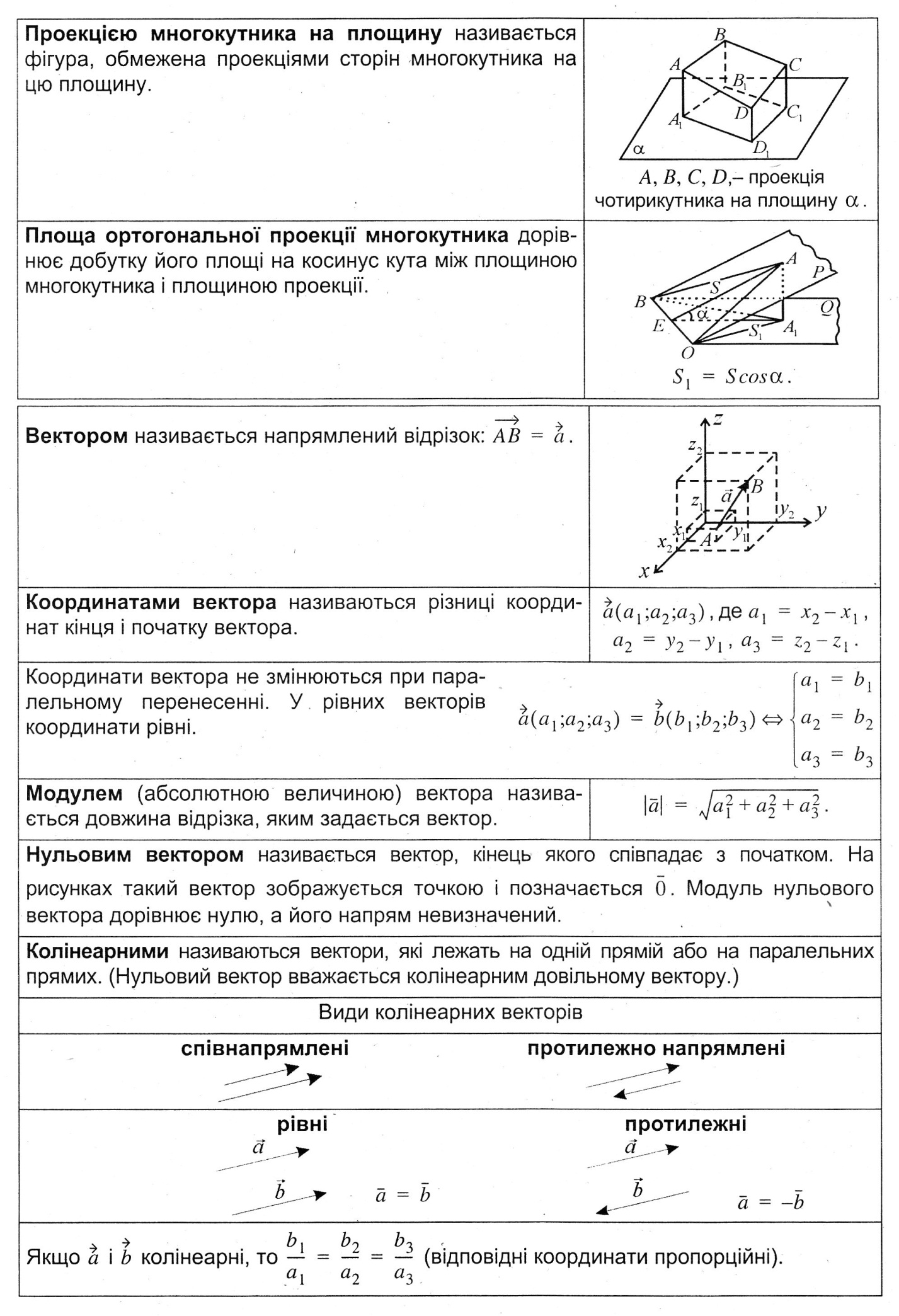
4 Кути у просторі.
Кутом між площинами  і
і 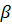 , які перетинаються по прямій
, які перетинаються по прямій 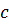 , називається кут між прямими, по яких третя площина
, називається кут між прямими, по яких третя площина 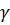 , яка перпендикулярна до лінії перетину, перетинає площини
, яка перпендикулярна до лінії перетину, перетинає площини  і
і 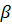 .
.
 Для побудови кута між площинами достатньо вибрати точку на ребрі утвореного двогранного кута (лінія перетину двох площин) і провести перпендикуляри в кожній із заданих площин. Кут між побудованими перпендикулярами і буде кутом між заданими площинами.
Для побудови кута між площинами достатньо вибрати точку на ребрі утвореного двогранного кута (лінія перетину двох площин) і провести перпендикуляри в кожній із заданих площин. Кут між побудованими перпендикулярами і буде кутом між заданими площинами.
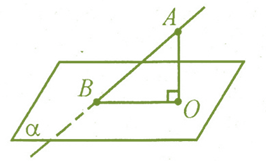
Кутом між прямою і площиною, яка її перетинає, називається кут між цією прямою та її проекцією на цю площину.
Отже, для побудови такого кута необхідно побудувати перпендикуляр з будь-якої точки заданої прямої на задану площину і проекцію прямої на площину. Кут між побудованою проекцією і заданою прямою буде шуканим кутом між прямою і площиною.
Кут між паралельними прямими і площинами вважається рівним 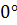 .
.
Кут між перпендикулярними прямою і площиною становить 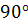 .
.
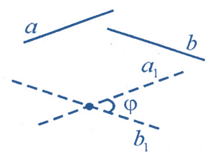 Кутом між мимобіжними прямими називається кут між прямими, які перетинаються і паралельні даним мимобіжним прямим.
Кутом між мимобіжними прямими називається кут між прямими, які перетинаються і паралельні даним мимобіжним прямим.
Якщо кут між мимобіжними прямими дорівнює 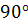 , то їх називають перпендикулярними.
, то їх називають перпендикулярними.


|
|
