Преобразования к линейному виду функций одной переменной.

I) Уравнение:

Координаты прямой:

Ось х: x

Ось y: 1\y

Уравнение прямой:

Значения:

Асимптоты:

____________________________________________________________________________________________________

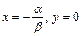
II) Уравнение:

Координаты прямой:

Ось х: 1\ x

Ось y: y

Уравнение прямой:

Значения:

Асимптоты:

____________________________________________________________________________________________________

III) Уравнение:

или

или

Координаты прямой:

Ось х: 1\ x

Ось y: 1\ y

Уравнение прямой:

Значения:

Асимптоты:

III a) Уравнение:

Координаты прямой:

Ось х: x

Ось y:

где

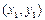- любая

точка на экспериментальной кривой

Уравнение прямой:

Значения:

Асимптоты:

Та же кривая, что и в 3), сдвинутая

вверх или вниз на расстояние .

____________________________________________________________________________________________________

IV) Уравнение:

Координаты прямой:

Ось х: log x

Ось y: log y

Уравнение прямой:

Значения:

Если , кривая

имеет вид параболы и проходит через начало координат и точку .

Если , кривая является гиперболой

с осями координат в качестве асимптот и проходит через точку .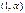

____________________________________________________________________________________________________

IV a) Уравнение:

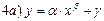
Координаты прямой:

Ось х: log x

Ось y:

Уравнение прямой:

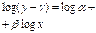
Значения:

Сначала аппроксимируем

по формуле

,

где

, а

- экспериментальные точки.

____________________________________________________________________________________________________

IV b) Уравнение:

Координаты прямой:

Ось х: log x

Ось y:

Уравнение прямой:

Значения:

После логарифмирования исходного уравнения поступают, как в п. 4а)

V) Уравнение:

Координаты прямой:

Ось х: x

Ось y: log y

Уравнение прямой:

Значения:

Кривая проходит

через точку .

Критерий МНК имеет вид:

где и рассчитываются при одном и том же значении элементов вектора

n – общее число опытов или объём выборки.

Согласно уравнению (3) и поэтому критерий Cr также является функцией многих переменных от параметров :

Для определения (подгонки) коэффициентов (параметров) модели (3) необходимо, чтобы критерий Cr стал наименьшим, т.е. чтобы сумма квадратов вертикальных отрезков на рисунке стала наименьшей:

Поэтому задача определения коэффициентов модели (3) сводится к реализации одного из алгоритмов оптимизации для определения минимума критерия (15) и (16):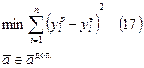

- допустимая область изменения параметров - ограничения первого рода.

Именно так решается задача параметрической идентификации для нелинейных моделей.

Конечно, в данном случае возможно также воспользоваться необходимым условием экстремума функции многих переменных (16):

Для определения искомых коэффициентов система в общем случае нелинейных уравнений (18) должна быть решена относительно коэффициентов a₀, a₁, …a_m.

Однако, как показывает практика, решение систем нелинейных уравнений ничуть не проще, чем прямое решение задачи оптимизации (17).

Определение выборочных (эмпирических) коэффициентов регрессии

для линейных по параметрам моделей (произвольное число входных переменных

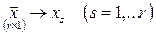
Таблица проведения экспериментальных исследований в этом случае имеет вид:

Для линейных или линеаризованных по параметрам моделей необходимо выражение (6) подставить в критерий МНК (15):

и, воспользовавшись необходимым условием экстремума функции многих переменных (18), решать полученную систему линейных алгебраических уравнений (СЛАУ):

Перегруппировав члены в системе уравнений (20), можно записать СЛАУ в виде:

И если ввести в рассмотрение информационную матрицу :

то она окажется квадратной, симметричной и значения её элементов зависят только от входных переменных и конкретного вида функций .

В матричном виде информационную матрицу можно представить в виде произведения трансформированной и исходной матрицы входных переменных :

Матрица, зависящая от входных переменных, имеет вид:

Соответственно правую часть СЛАУ (21) можно записать:

или в матричном виде:

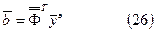
В результате СЛАУ (21), решаемая для определения коэффициентов эмпирической модели, может быть представлена:

или в матричном виде:

Если для определения коэффициентов использовать метод обратной матрицы, то получится:

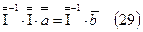
и так как произведение равно единичной матрице , т.е.

то

или

Матричная формула для определения коэффициентов линейной регрессии (параметров эмпирической модели) получается после подстановки в (32) матричных равенств (23) и (26):

Таким образом для определения коэффициентов линейной или линеаризованной регрессионной модели необходимо выполнить следующую последовательность действий:
сформировать вектор наблюдений и вычислить его компоненты (только для линеаризованных моделей);

сформировать и рассчитать компоненты матрицы, зависящей от входных переменных ;
транспонировать матрицу ;

перемножить транспонированную матрицу 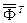на исходную матрицу ;

выполнить обращение информационной матрицы - ;

умножить полученную обратную матрицу на матрицу ;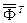

умножить полученный результат на вектор наблюдений и получить выборочные коэффициенты регрессии (33).