Построение эмпирических моделей по данным пассивного эксперимента

2.1. Определение вида приближённого уравнения регрессии

В общем случае необходимо анализировать графики зависимостей экспериментальных данных выходных переменных y от входных x и по их виду выбирать конкретную форму функциональной зависимости (3).

Преобразование системы координат y – x даёт возможность выбрать оптимальный вид функциональной зависимости (3).

Для случая одной входной переменной х по опытным данным рекомендуется построить эмпирическую линию регрессии (рис.1) и с её помощью выбирать конкретный вид функции (3).

Изображение эмпирической линии регрессии:

При этом весь диапазон изменения x (рис.1) разбивается на s равных интервалов Δ x. Все точки, попавшие в данный интервал Δ x_j, относят к его середине x_j^*. После этого подсчитывают частные средние y_j^* для каждого интервала:

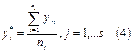
где n_j – число точек в интервале Δ x_j.

В результате объём выборки определяется по формуле:

Эмпирическая линия регрессии y по x получается в виде ломанной линии путём последовательного соединения отрезками прямой линии точек:

При выборе вида функции (3) для случая нескольких входных переменных

может быть применён метод Брандона, который здесь не рассматривается.

В общем случае различают два вида уравнений регрессии (эмпирических моделей) – нелинейные по параметрам , статистический анализ которых осуществляется методом «нелинейной регрессии» и линейные по параметрам , статистический анализ которых проводится методом «линейной регрессии».

Линейные по параметрам модели могут быть представлены в следующем виде:

где - линейные или нелинейные функции входных переменных ( ).

Определение параметров (коэффициентов) линейных моделей и их регрессионный анализ существенно проще, чем для нелинейных моделей.

Поэтому нелинейные модели, по возможности, стараются линеаризовать и привести к виду (6).

Частными случаями уравнения линейной регрессии являются:

А) полиномиальная регрессия, когда

и её разновидности – линейная регрессия от одной переменной (m =1):

и параболическая регрессия (m =2):

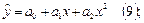
Б) трансцендентная регрессия и её разновидности в виде зависимости показательного типа:

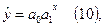
которая линеаризуется логарифмически:

и дробно-показательного типа:

которая также линеаризуется логарифмически:

В) множественная регрессия, когда число входных переменных больше 1:

2.2. Определение коэффициентов регрессии – параметров эмпирических моделей (выполнение первого этапа регрессионного анализа).

В соответствии с методологией регрессионного анализа в этом случае решается задача аппроксимации экспериментальных данных методом наименьших квадратов (МНК).

На рисунке приведена графическая интерпретация МНК для случая регрессии от одной переменной х (* - экспериментальные данные, - расчётные данные по уравнению регрессии):

При этом эксперимент проводится с использованием следующей таблицы:

Вид функции одной переменной может быть выбран (решение задачи структурной идентификации) путём преобразования осей координат у – х как показано ниже.

В результате преобразованная функция у становится линейной не только по коэффициентам регрессии, но и по преобразованной переменной х.