Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Многомолекулярная локализованная адсорбция. Изотерма адсорбции Ленгмюра.

Мономолекулярная адсорбция — адсорбция происходит в один слой. Локализованная адсорбция — если адсорбированные молекулы закреплены на адсорбционных центрах и при этом выделяется максимум энергии.

Модель Ленгмюра: 1) Если молекула попадает на свободный адсорбционный центр, то она остается на нем. 2) Если молекула попадает на занятый адсорбционный центр, то она уходит с поверхности. 3) Адсорбирование имеет место только на определенные адсорбционные центры. 4) Если все адсорбционные центры заняты, то наступает предел адсорбции.

- число адсорбционных центров на единицу поверхности.

- число занятых адсорбционных центров на единицу поверхности.

- число доступных для адсорбции адсорбционных центров на единицу поверхности.

Вероятность того, что молекула, ударяющаяся о поверхность будет адсорбирована равна: И з кинетической теории газов. Число адсорбированных молекул в единицу времени: Если это выражение помножить на время жизни одной адсорбированной молекулы, то получим выражение, которое показывает число молекул, находящихся в поверхности:

Степень заполняемости поверхности: И введем обозначение:

Данное выражение показывает зависимость адсорбции от давления при постоянной температуре и носит название изотермы адсорбции Ленгмюра.

Полимолекулярная адсорбция. Полимолекулярная адсорбция характерна для адсорбции газов, в случае, если газы не реагируют с поверхностью и не разлагаются на ней.

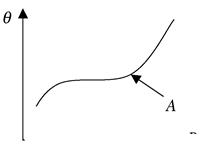
Теплота адсорбции 2 слоя атомов или молекул очень мала. Изотермы паров при Т < Ткип часто имеют S -образную форму. В точке A внешнее давление приближается к давлению насыщенных паров и происходит объемная конденсация паров. Такая адсорбция называется /Т < Т/ полимолекулярной. Для того, чтобы имела место полимолекулярная адсорбция, необходимо, чтобы время жизни молекул второго слоя было соизмеримо со временем изни молекул первого слоя. В противном случае (Т2 < ТХ) наблюдается ономолекулярная адсорбция. Взаимодействие между (1 и 2), (2 и 3) и т.д. слоями определяется энергией конденсации. При адсорбции пара молекулы, попадая на уже занятую поверхность, образуют адсорбционные комплексы второго слоя. Между молекулами одного слоя и молекулами следующего слоя существует взаимодействие и оно постоянно для молекул этих двух слоев. Молекулы любого отдельно взятого слоя не взаимодействуют друг с другом. Начиная со второго слоя адсорбция и десорбция протекают так же как в жидкостях и теплота адсорбции равна теплоте конденсации.

Уравнение изотермы Брунауэра-Эммета-Теллера

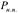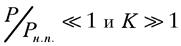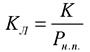- текущее давление. - давление насыщенных паров. Если , то уравнение БЭТ упрощается: Принимая при данных условиях БЭТ вырождается в уравнение адсорбции Ленгмюра. Таким образом уравнение адсорбции Ленгмюра описывает адсорбцию при давлениях пара гораздо меньших, чем давление насыщенного пара.

Диффузия. Определение и основные понятия.

Диффузия — процесс переноса материи или энергии из области с высокой концентрацией в область с низкой концентрацией. Самым известным примером диффузии является перемешивание газов или жидкостей. Все виды диффузии подчиняются одинаковым законам. Скорость диффузии пропорциональна площади поперечного сечения образца, а также разности концентраций, температур или зарядов (в случае относительно небольших величин этих параметров). Так тепло будет в четыре раза быстрее распространяться через стержень с диаметром в два сантиметра, чем через стержень с диаметром в один сантиметр. Это тепло будет распространяться в два раза быстрее, если перепад температур на одном сантиметре будет 10 º C вместо 5 º C. Скорость диффузии пропорциональна также параметру, характеризующему конкретный материал. В случае тепловой диффузии этот параметр называется теплопроводность, в случае потока электрических зарядов — электропроводность. Количество вещества, которое диффундирует в течение определённого времени и расстояние, проходимое диффундирующим веществом, пропорциональны квадратному корню времени. Диффузия представляет собой процесс на молекулярном уровне и определяется случайным характером движения отдельных молекул. Скорость диффузии пропорциональна в связи с этим средней скорости молекул. В случае газов средняя скорость малых молекул больше, а именно она обратно пропорциональна квадратному корню из массы молекулы и растёт с повышением температуры. Диффузионные процессы в твёрдых телах при высоких температурах часто находят практическое применение. С точки зрения термодинамики движущим потенциалом любого выравнивающего процесса является рост энтропии. При постоянных давлении и температуре в роли такого потенциала выступает химический потенциал µ, обуславливающий поддержание потоков вещества. Поток частиц вещества пропорционален при этом градиенту потенциала J ~ . В большинстве практических случаев вместо химического потенциала применяется концентрация C. Прямая замена µ на C становится некорректной в случае малых концентраций, так как химический потенциал связан с концентрацией по логарифмическому закону. Если не рассматривать такие случаи, то выше приведённую формулу можно заменить на следующую: . которая показывает, что плотность потока вещества J [cm - 2s - 1] пропорциональна коэффициенту диффузии D [(cm2s - 1)] и градиенту концентрации. Это уравнение выражает первый закон Фика (Адольф Фик — немецкий физиолог, установивший законы диффузии в 1855 г.). Второй закон Фика связывает пространственное и временное изменения концентрации (уравнение диффузии): . Коэффициент диффузии D зависит от температуры. В ряде случаев в широком интервале температур эта зависимость представляет собой уравнение Аррениуса. Дополнительное поле, наложенное параллельно градиенту химического потенциала, нарушает стационарное состояние. В этом случае диффузионные процессы описываются нелинейным уравнением Фоккерa—Планка