Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Уравнение Клапейрона — Клаузиуса

Уравнение Клапейрона-Клаузиуса — основное уравнение, описывающее фазовые превращения.

Рассмотрим G = H-TS - энергию Гиббса, так как процесс изотермический для индивидуального вещества.

Энтальпия есть H = U + PV, тогда

G = U + PV - TS. Продифференцируем:

dG = dU + PdV + VdP - TdS - SdT

Рассмотрим изолированную систему, находящуюся в равновесии (например, жидкость-пар). Равновесие заключается в том, что за единицу времени определенное число молекул переходит из жидкой фазы в газообразную. За это же самое время ровно такое же число молекул переходит из газообразной фазы в жидкую.

Это значит, что

- химический потенциал компонента системы.

В изолированной системе равновесие при dS = 0.

Также учтем, что

dG=dU+PdV+VdP-TdS-SdT (dU=0; dV=0; dS=0)

dG=VdP-SdT

dG1=V1dP-S1dT

dG2=V2dP-S2dT

Перейдем к конечным разностям AG = VAP - SAT. Рассмотрим две фазы:

Вычтем из выражения (2) выражение (1):

- изменение энтропии при фазовом переходе;

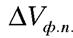
- изменение объема при фазовом переходе;

Так как температура фазового перехода зависит от давления, то индекс ф.п. опускаем.

Клапейрона — Клаузиуса уравнение, термодинамическое уравнение, относящееся к процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно К. — К. у теплота фазового перехода (например, теплота испарения, теплота плавления) при равновесно протекающем процессе определяется выражением

, (1)

где Т — температура перехода (процесс изотермический), dp/dT — значение производной от давления по температуре при данной температуре перехода, (V₂—V₁) — изменение объёма вещества при переходе его из первой фазы во вторую.

Первоначально уравнение было получено в 1834 Б. П. Э. Клапейроном из анализа Карно цикла для конденсирующегося пара, находящегося в тепловом равновесии с жидкостью. В 1850 P. Клаузиус усовершенствовал уравнение и распространил его на др. фазовые переходы. К. — К. у. применимо к любым фазовым переходам, сопровождающимся поглощением или выделением теплоты (т. н. фазовым переходом 1 рода), и является прямым следствием условий фазового равновесия, из которых оно и выводится.

К. — К. у. может служить для расчёта любой из величин, входящих в уравнение, если остальные известны. В частности, с его помощью рассчитывают теплоты испарения, экспериментальное определение которых сопряжено со значительными трудностями.

Часто К. — К. у. записывают относительно производных dp/dT или dT/dp:

(2)

Для процессов испарения и сублимации dp/dT выражает изменение давления насыщенного пара р с температурой Т, а для процессов плавления и полиморфного превращения dT/dp определяет изменение температуры перехода с давлением. Иными словами, К. — К. у. является дифференциальным уравнением кривой фазового равновесия в переменных р, Т.

Для решения К. — К. у. необходимо знать, как изменяются с температурой и давлением величины L, V₁ и V₂, что представляет сложную задачу. Обычно эту зависимость устанавливают эмпирически и решают К. — К. у. численно.

К. — К. у. применимо как к чистым веществам, так и к растворам и отдельным компонентам растворов. В последнем случае К. — К. у. связывает парциальное давление насыщенного пара данного компонента с его парциальной теплотой испарения.

24. Фазовое равновесие: твердое кристаллическое тело — жидкость.

ФАЗОВОЕ РАВНОВЕСИЕ, сосуществование термодинамические равновесных фаз гетерогенной системы. Является одним из основных случаев термодинамического равновесия и включает в себя условия равенства т-ры всех частей системы (термич. равновесие), равенства давления во всем объеме системы (мех. равновесие) и равенство хим. потенциалов каждого компонента во всех фазах системы, что обеспечивает равновесное распределение компонентов между фазами. Число фаз f, находящихся одновременно в равновесии, связано с числом компонентов k, числом n независимых параметров, определяющих состояние системы (обычно, когда учитывается только влияние т-ры и давления, n = 2), и числом термодинамич. степеней свободы v ур-нием: v = k + 2 - f (см. Фаз правило).[Равновесие процесса перехода в-ва из одной фазы в другую без изменения хим. состава – фаз. равновесие]

В общем виде условие Ф. р., согласно принципу равновесия Гиббса, сводится к максимуму энтропии S системы при постоянстве внутр. энергии U, общего объема V и числа молей каждого компонента n_i-. Этот принцип можно выразить также как условие минимума любого из термодинамич. потенциалов: внутр. энергии U, энтальпии H, энергии Гиббса G, энергии Гельмгольца А при условии постоянства соответствующих параметров состояния, включая число молей каждого компонента. Ф.р. могут быть стабильными и метастабильными.

Твердое кристаллическое тело Жидкость; Вэтом случае изменения объема и

Как правило, объем жидкости превышает объем твердого тела:

Ввыражении (1) - величина большая, поэтому , но величина малая.

Для каждого вещества существует свой барический коэффициент температуры плавления.

Например, для бензола Δ T/Δ P=0.00285 K/атм. Это значит, что если твердый бензол сжать до давления в 1000 атм., то температура плавления изменится на 2, 85 К.

25. Фазовое равновесие: жидкость — пар.

- уравнение Клайперона-Клаузиуса.

 

Соответственно неизвестны для химической термодинамики, известно лишь изменение энтальпии Определим зависимость давления насыщенного пара от температуры . Примем три допущения для решения уравнения Клаузиуса-Клапейрона: 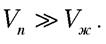Это легко показать: 1 моль весит 18 г, а занимает объем V = 22, 4 л. 2) В узком температурном интервале тепловой эффект испарения Δ Н_исп не зависит от температуры. 3) Считаем пар идеальным газом, для 1 моля которого выполняется закон Менделеева-Клапейрона Тогда, учитывая допущения, уравнение Клаузиуса-Клайперона примет вид:

разделим переменные:

 

рисунок 2

 

Давление насыщенного пара над жидкостью не зависит от количества жидкости и определяется только температурой. Значения давления насыщенного пара для различных жидкостей сведены в таблицы. Кипение - это процесс парообразования (испарения) по всему объему жидкости, а не только с ее поверхности. Кипение имеет место, когда P н.п = Р внеш. (рис 1)

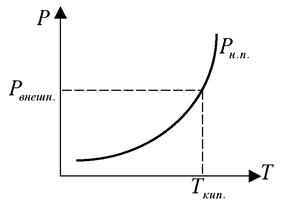
рис 1 рис 2

26.Фазовое равновесие: твердое тело — пар.

Процесс (1) называется сублимация или возгонка. А процесс (2) — конденсация. Для многих твердых веществ давление насыщенного пара очень мало. Основное условие измерения давления насыщенного пара твердого тела: в системе должно быть только твердое тело и его пар.

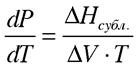- уравнение Клапейрона-Клаузиуса для данного случая.

П о закону Гесса: Δ Н _{су 6 л} =Δ Н_плавл + Δ Н_исп, — данное равенство соблюдается точно, когда в равновесии находятся все три фазы. Примем три допущения для решения уравнения Клаузиуса-Клайперона:

4)

5)В узком температурном интервале тепловой эффект испарения не зависит от температуры;

6) Считаем пар идеальным газом, для 1 моля которого выполняется закон Менделеева-Клайперона 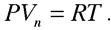Тогда, учитывая допущения, уравнение Клаузиуса-Клайперона примет вид:

Таким образом экспериментально можно определить теплоту сублимации. разделим переменные:

 

27. Правило фаз Гиббса. Диаграмма состояния однокомпонентной системы .

Компонентом называется химически однородная составная часть вещества, которая может быть выведена из системы. Диаграммами состояния (фазовыми диаграммами) называются диаграммы, по которым можно определить условия устойчивости фаз и фазового равновесия. В качестве примера диаграммы состояния однокомпонентной системы рассмотрим диаграмму состояния воды. Каждая точка поля диаграммы состояний характеризуется парой чисел P и Т. AO - зависимость давления насыщенного пара твердого тела от температуры OD - зависимость

OB -

AO - равновесие тв.тело пар

OD - равновесие жидкость пар

OB - равновесие тв.тело жидкость

В о всех других точках диаграммы состояний, которые не лежат на перечисленных

кривых, система существует в виде одной фазы. В точке О в равновесии существуют все три фазы. Эта точка называется тройной. Обозначим через Ф - число фаз системы. Пусть / - число степеней свободы, то есть число параметров, которые можно менять, не меняя состояния системы. К - число независимых компонентов системы. Также через п обозначим число внешних условий, влияющих на равновесие (как правило, давление и температура, т.е. п = 2). Правило фаз Гиббса: