Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Задача №53

Побудувати проекції наскрізних отворів

а) б)

в) г)

д) е)

ж) з)

5.5 Контрольний тест до інформаційного модуля 5

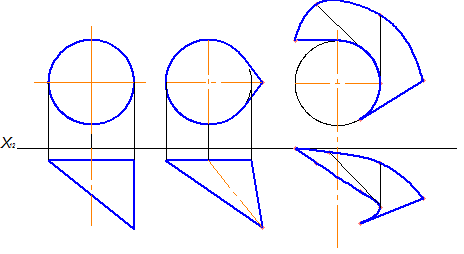
1. Які з показаних поверхонь відносяться до поверхонь обертання?

а) б) в)

2. На якому рисунку показано поверхню Каталану?

а) б) в)

3. На якому рисунку точка А належить поверхні?

а) б) в)

4. На якому рисунку лінія ℓ належить поверхні?

а) б) в)

5. На якому рисунку січна площина перетинає задану поверхню по еліпсу?

а) б) в)

ІНФОРМАЦІЙНИЙ МОДУЛЬ 6

ПОЗИЦІЙНІ ЗАДАЧІ НА ПРЯМОКУТНИХ ПРОЕКЦІЯХ ПОВЕРХОНЬ

6.1 Третя позиційна задача

Третя позиційна задача – це задача на перетин поверхні з площиною. Якщо площина займає проекціювальне положення, то одна з проекцій лінії перетину збігається із слід-проекцією площини в межах заданої поверхні. Далі розв’язування зводиться до побудови інших проекцій точок, що належать поверхні (див. тему 5). Якщо площина займає загальне положення, то для розв’язування задачі треба застосувати спеціальні методи, наприклад, метод заміни площин проекцій. При цьому додаткова площина вводиться таким чином, щоб задана площина перетворилася в проекціювальну.

Рисунок 6.1 – Побудова лінії перетину циліндра площиною загального положення (наочне зображення)

Приклад розв’язування (рис.6.1, 6.2):

1) вводимо додаткову площину проекцій X₁₄, що перпендикулярна до горизонтальної проекції горизонталі_, h₁;

2) проекціюємо циліндр на додаткову площину Π ₄;

3) проекціюємо площину на додаткову площину Π ₄;

4) визначаємо лінію перетину, проекція якої збігається з проекцією пло-щини на Π ₄ в межах проекції циліндра (1₄ – 3₄);

5) знаходимо проекції точок, що належать даній лінії, послідовно на Π ₁ та Π ₂, враховуючи при цьому, що відстані в Π ₁ від Х_{1, 2} до відповідної проекції і відстані в Π ₄ від Х _{1, 4} до відповідної проекції рівні між собою;

6) обов’язково визначаємо точки 2 і 5, оскільки саме вони визначають границю видимості на Π ₂.

Рисунок 6.2 – Побудова лінії перетину циліндра площиною загального положення (проекційне креслення)

Необхідно відмітити, що введена допоміжна площина проекцій може бути перпендикулярна як до Π ₁, так і до Π ₂. При цьому необхідно враховувати складність проекціювання також і самої поверхні.

У випадках, якщо поверхнею є конус, сфера та таке ін., необхідно будувати також і горизонтальну проекцію лінії перетину поверхні з площиною, використовуючи при цьому твірні або паралелі.

Задачі для самостійного розв’язування