Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача № 59

Побудувати лінію перетину

поверхні обертання площиною,

що задана трикутником.

6.2 Четверта позиційна задача

В загальному випадку ця задача формулюється так: визначити проекції точок перетину лінії (кривої або прямої) з поверхнею. Розглянемо алгоритми розв’язання задачі, коли необхідно визначити проекції точок перетину прямих ліній різного положення з поверхнями.

Алгоритм 1 - Пряма займає проекціювальне положення.

При такому розташуванні прямої відносно системи площин проекцій одна проекція шуканих точок збігається з виродженою проекцією самої прямої, а дві інші визначають за умови належності поверхні, яку перетинає пряма. Тобто, алгоритм реалізовує принцип одночасної належності шуканих точок двом геометричним фігурам - проекціювальній прямій та поверхні. На рис.6.3 показано циліндричну поверхню і пряму ℓ, яка займає фронтально-проекціювальне положення та перетинає циліндр в точках K і L. Тому фронтальні проекції K2 і L2 шуканих точок перетину лінії ℓ з циліндричною поверхнею збігаються з фронтальною проекцією заданої прямої лінії ℓ 2. Горизонтальні проекції K1 і L1 визначені за умови належності точок відповідним твірним циліндра.

Рисунок 6.3 - Перетин прямої лінії з циліндром

На рис. 6.4 проілюстровано алгоритм визначення проекцій точки перетину прямої ℓ, яка займає горизонтально-проекціювальне положення, з конусом.

Рисунок 6.4 - Перетин прямої лінії з конусом обертання

Алгоритм 2 – Пряма займає загальне положення або положення рівня.

При такому розташуванні прямої лінії визначення проекцій точок її перетину з поверхнею передбачає виконання таких геометричних операцій:

- проведення через пряму допоміжної січної площини (частіше за все – проекціювальної) – на рис.6.5, а така площина позначена «Т»;

- побудова лінії перерізу поверхні допоміжною площиною – на рис.6.5, б лінія перерізу позначена «а»;

- визначення шуканих точок як точок перетину побудованої лінії перерізу та заданої прямої, на рис. 6.5 такими точками є точки К і L.

На рис. 6.5, в показано реалізацію наведеного алгоритму для визначення прямокутних проекцій точок перетину лінії загального положення ℓ з поверхнею обертання θ, використовуючи допоміжну січну фронтально-проекціювальну площину Т.

а)

б) в)

Рисунок 6. 5 - Перетин прямої загального положення з поверхнею обертання

В деяких випадках, особливо для визначення точок перетину прямих з лінійчатими поверхнями, найбільш ефективним є використання допоміжних січних площин - площин загального положення. Доцільність їх використання - отримати переріз поверхні площиною якомога простіший за формою. На рис. 6.6 показано використання допоміжної січної площини загального положення для визначення точок перетину прямої ℓ з еліптичним конусом. Така площина утворена прямими a і ℓ, які перетинаються в точці А, проходить через вершину S і перерізає конус по твірних S1 і S2. Фігуру перерізу знайдено за допомогою попередньо визначеного сліду січної площини на Π 1 (пряма MN). Шукані точки K і L є точками перетину побудованого перерізу і заданої прямої.

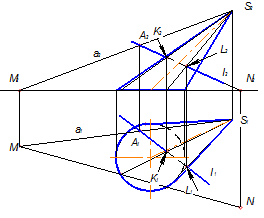
Рисунок 6.6 - Визначення точок перетину прямої з еліптичним конусом

Окремим випадком можна вважати визначення точок перетину прямої з проекціювальним циліндром (циліндром, у якого твірні займають проекціювальне положення), оскільки шукані точки визначають як точки, що одночасно належать циліндричній поверхні та прямій (рис. 6.7).

Рисунок 6.7 – Визначення точок перетину прямої з циліндром

Задачі для самостійного розв’язування