
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение прямой. Способы задания прямой. Взаимное расположение прямых
|
|
Задача 1 Построить и составить уравнение прямой 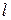 :
:
а)  ,
,  ; б)
; б)  ,
,  ;
;
в)  ,
,  ; г)
; г) 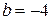 ,
,  ;
;
д)  ,
,  ; е) т.
; е) т.  ,
,  ;
;
ж) проходящей через 2 различные точки  и
и  ;
;
з) проходящей через точку  перпендикулярно прямой
перпендикулярно прямой 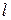 , проходящей через точки
, проходящей через точки  и
и 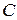 , где
, где  ,
,  ;
;
и) проходящей точка  параллельно прямой
параллельно прямой 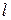 , проходящей через точки
, проходящей через точки  и
и 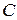 , где
, где  ,
,  ;
;
к) проходящей через точку 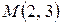 и направляющий вектор
и направляющий вектор  ;
;
л) проходящей через точку  с нормальным вектором
с нормальным вектором  .
.
 Решение. а) Так как
Решение. а) Так как  (
( - ордината точки пересечения прямой с осью
- ордината точки пересечения прямой с осью 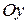 ) и
) и  (
( - угол, который прямая образует с положительным направлением оси
- угол, который прямая образует с положительным направлением оси  ). Воспользуемся формулой уравнением прямой с угловым коэффициентом
). Воспользуемся формулой уравнением прямой с угловым коэффициентом  .
.
 ,
,
 .
.
Ответ.  Рисунок 18
Рисунок 18
 б) Так как
б) Так как  (
( - ордината точки пересечения прямой с осью
- ордината точки пересечения прямой с осью 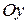 ) и
) и  (
( - угол, который прямая образует с положительным направлением оси
- угол, который прямая образует с положительным направлением оси  ). Воспользуемся формулой уравнением прямой с угловым коэффициентом
). Воспользуемся формулой уравнением прямой с угловым коэффициентом 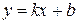 .
.
 ,
,
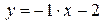
 .
.
Ответ.  Рисунок 19
Рисунок 19
в) Так как 
 (
( - расстояние, которое отсекает прямая на оси
- расстояние, которое отсекает прямая на оси  ) и
) и  , т.е. прямая перпендикулярно оси
, т.е. прямая перпендикулярно оси 
 .
.

Ответ.  Рисунок 20
Рисунок 20
г) Так как 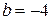 ,
, 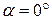 . Воспользуемся формулой уравнением прямой с угловым коэффициентом
. Воспользуемся формулой уравнением прямой с угловым коэффициентом 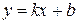 .
.
 .
.
 |
Ответ.  Рисунок 21
Рисунок 21
д) Так как  ,
,  (
( - угловой коэффициент прямой). Воспользуемся формулой уравнением прямой с угловым коэффициентом
- угловой коэффициент прямой). Воспользуемся формулой уравнением прямой с угловым коэффициентом
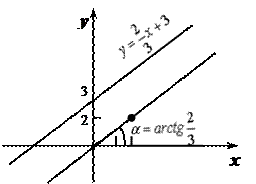
 .
.
| |||
| |||
Ответ.  Рисунок 22
Рисунок 22
е) Так как дана точка  лежащая на прямой и угловой коэффициент
лежащая на прямой и угловой коэффициент  , воспользуемся формулой
, воспользуемся формулой 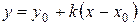

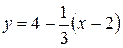 ,
,  ,
,
 .
.
Ответ.  Рисунок 23
Рисунок 23
 ж) Уравнение прямой, проходящей через две различные точки
ж) Уравнение прямой, проходящей через две различные точки  и
и  выглядит следующим образом:
выглядит следующим образом:
 .
.
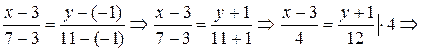

 Рисунок 24
Рисунок 24
 .
.
Ответ. 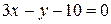
з) Уравнение прямой, проходящей через т.  перпендикулярно прямой
перпендикулярно прямой  , где
, где  ,
,  выглядит следующим образом:
выглядит следующим образом:
Составим уравнение прямой  :
:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
 .
.
 .
.
 Уравнение
Уравнение  :
:  . Угловой коэффициент прямой
. Угловой коэффициент прямой  :
:  . Так как прямые перпендикулярны, то их угловые коэффициенты противоположны по знаку и обратны по значению, т.е.
. Так как прямые перпендикулярны, то их угловые коэффициенты противоположны по знаку и обратны по значению, т.е. 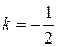 . Воспользуемся формулой
. Воспользуемся формулой 
 .
.
Ответ.  Рисунок 25
Рисунок 25
и) Уравнение прямой  составили в предыдущем примере
составили в предыдущем примере  :
:  .
.
Так как по условию две прямые параллельны, то их угловые коэффициенты равны, т.е. 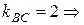 угловой коэффициент для нашей прямой будет тоже равен 2.
угловой коэффициент для нашей прямой будет тоже равен 2.
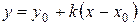 ,
,
 .
.
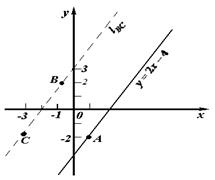
Ответ.  Рисунок 26
Рисунок 26
 к) Уравнение прямой, проходящей через точку
к) Уравнение прямой, проходящей через точку 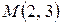 и направляющий вектор
и направляющий вектор  задается уравнением:
задается уравнением: 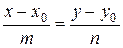 .
.
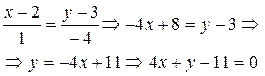
Ответ. 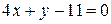 Рисунок 27
Рисунок 27
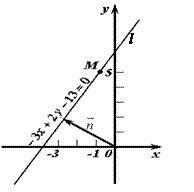 л) Общее уравнение прямой, проходящей через точку с нормальным вектором
л) Общее уравнение прямой, проходящей через точку с нормальным вектором 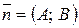 , выглядит следующим образом:
, выглядит следующим образом:  . Таким образом, уравнение прямой, проходящей через т.
. Таким образом, уравнение прямой, проходящей через т.  с нормальным вектором
с нормальным вектором  ,
,  будет следующим:
будет следующим:
 ,
,
 .
.
Ответ.  Рисунок 28
Рисунок 28
Задача 2 Определить взаимное расположение прямых:
а) 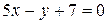 ,
,  ; б)
; б)  ,
,  ;
;
в)  ,
,  , г)
, г)  ,
,  .
.
Решение. а) 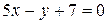 ,
,  .
.
1 способ. Найдем угол между двумя прямыми, если прямые заданы через угловые коэффициенты. От общего уравнения прямой 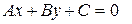
 перейдем к уравнению прямой через угловой коэффициент
перейдем к уравнению прямой через угловой коэффициент 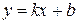

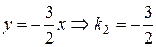 и воспользуемся формулой
и воспользуемся формулой 
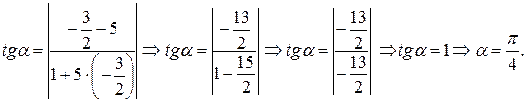
2 способ. Найдем угол между двумя прямыми, если прямые заданы в общем виде:  .
.
 ,
,  Воспользуемся формулой
Воспользуемся формулой 

 .
.
Ответ. 
б)  ,
,  .
.
1 способ. Аналогично, от общего уравнения прямой 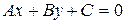
перейдем к уравнению прямой через угловой коэффициент 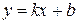
 :
:  .
.  Угловые коэффициенты противоположны по знаку и обратны по значению или
Угловые коэффициенты противоположны по знаку и обратны по значению или  . Следовательно, прямые перпендикулярны, т.е. угол между ними
. Следовательно, прямые перпендикулярны, т.е. угол между ними  .
.
2 способ. Прямые заданы в общем виде 


 . Найдем скалярное произведение векторов
. Найдем скалярное произведение векторов  и
и  :
:  нормальные вектора
нормальные вектора  и
и  перпендикулярны
перпендикулярны  прямые пересекаются под углом
прямые пересекаются под углом  .
.
Ответ. 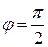
в)  ,
,  .
.
1 способ. Прямые заданы в общем виде 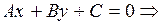
 ,
,  . Перейдем от общего уравнения прямой
. Перейдем от общего уравнения прямой 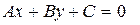


 к уравнению прямой через угловой коэффициент
к уравнению прямой через угловой коэффициент
и найдем угловые коэффициенты прямых

 Угловые коэффициенты равны, т.е.
Угловые коэффициенты равны, т.е. 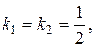
следовательно, прямые параллельны.
2 способ. Так как прямые заданы в общем виде  , то запишем координаты нормальных векторов
, то запишем координаты нормальных векторов  и
и  :
: 

 . Так как координаты векторов
. Так как координаты векторов  и
и  пропорциональны, то вектора коллинеарны
пропорциональны, то вектора коллинеарны  .
.
Нормальные вектора коллинеарны, следовательно, прямые параллельны.
Ответ. Прямые параллельны
г)  ,
,  .
.
1 способ. Перейдем от общего уравнения прямой 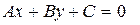


 к уравнению прямой через угловой коэффициент и найдем угловые коэффициенты прямых
к уравнению прямой через угловой коэффициент и найдем угловые коэффициенты прямых
 ,
,  ;
;  ,
, 
Следовательно, прямые совпадают, так как  и
и  .
.
2 способ. Так как прямые заданы в общем виде  , то запишем координаты нормальных векторов
, то запишем координаты нормальных векторов  и
и  :
: 
 . Так как координаты векторов
. Так как координаты векторов  и
и  пропорциональны
пропорциональны  и отношение свободных членов тоже равно
и отношение свободных членов тоже равно  , т. е.
, т. е.  . Таким образом, справедлива формула
. Таким образом, справедлива формула 
 прямые совпадают.
прямые совпадают.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Ответ. Прямые совпадают
Задача 3 При каких значениях  и
и 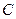 две прямые
две прямые  ,
, 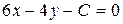
а) параллельны;
б) совпадают;
в) имеют общую точку.
Решение. Прямые на плоскости могут быть либо параллельными, т.е.  ; либо совпадать
; либо совпадать 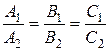 ; либо пересекаться
; либо пересекаться 
а) 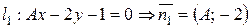 ,
,
 .
. 
 ;.
;.  .
.
б) прямые совпадают тогда и только тогда, когда 

 .
.
в) При  и
и  прямые имеют общую точку.
прямые имеют общую точку.
Ответ. а) при  и
и 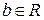 прямые параллельны;
прямые параллельны;
б) при  и
и  прямые совпадают;
прямые совпадают;
в) при  и
и  прямые имеют общую точку
прямые имеют общую точку
Задача 4 Привести общее уравнение прямой к нормальному виду:
а) 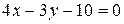 ; б)
; б)  ; в)
; в) 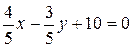 .
.
 Решение. а) Прямая задана в общем виде
Решение. а) Прямая задана в общем виде 
 Приведем к нормальному виду Найдем нормирующий множитель
Приведем к нормальному виду Найдем нормирующий множитель 
 . Так как
. Так как  , то
, то 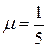 . Умножим общее уравнение на нормирующий множитель
. Умножим общее уравнение на нормирующий множитель  .
.
б)  ,
, 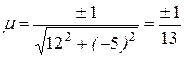
Так как  , то
, то  :
: 
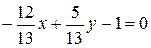 .
.
в)  ,
,  . Так как
. Так как  , то
, то  :
:  ,
,  .
.
Ответ. а) 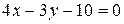 ; б)
; б) 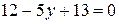 ; в)
; в) 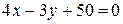
Задача 5 Вычислить расстояние  между прямыми:
между прямыми:
а)  ,
,  ; б)
; б)  ,
,  .
.
Решение. а)Исследуем данные прямые как они расположены друг относительно друга  ,
,  ,
,  .
.
Так как  прямые параллельны. Найдем расстояние между параллельными прямыми. На прямой
прямые параллельны. Найдем расстояние между параллельными прямыми. На прямой  найдем точку; пусть
найдем точку; пусть  , тогда
, тогда  . Точка
. Точка  .
.
По формуле  , найдем расстояние от точки
, найдем расстояние от точки  , т.е.
, т.е.  до прямой
до прямой  , т.е.
, т.е.  .
.

 .
.
б) Исследуем расположение данных прямых  и
и  .
.
 ,
,  ,
,
Используя формулу 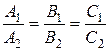
получим 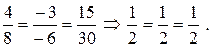 Следовательно, прямые совпадают и расстояние между ними равно нулю (
Следовательно, прямые совпадают и расстояние между ними равно нулю (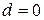 ).
).
Ответ. а)  ; б)
; б) 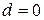
Задача 6 При каких значениях  следующие пары прямых
следующие пары прямых  и
и  : а) параллельны; б) перпендикулярны:
: а) параллельны; б) перпендикулярны:  :
:  и
и  :
:  ;
;
Решение. 1 способ. а)  и
и  .
.
Две прямые  и
и  параллельны (
параллельны ( ), если нормальные вектора
), если нормальные вектора  и
и  коллинеарны.
коллинеарны.  ,
, 

 .
.
б) Если две прямые  и
и  перпендикулярны (
перпендикулярны (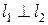 ), то нормальные вектора
), то нормальные вектора  и
и  ортогональны
ортогональны 
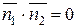 :
:  ,
, 
 ,
,  .
.
2 способ. Запишем уравнения прямых через угловые коэффициенты.
а)  ,
,  и
и  ,
, 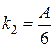
Прямые  , если угловые коэффициенты прямых равны. Приравняем угловые коэффициенты прямых
, если угловые коэффициенты прямых равны. Приравняем угловые коэффициенты прямых  .
.
б) Используем признак перпендикулярности двух прямых, если прямые заданы в общем виде. Прямые  перпендикулярны, если угловые коэффициенты прямых противоположны по знаку и обратны по значению
перпендикулярны, если угловые коэффициенты прямых противоположны по знаку и обратны по значению  ,
, 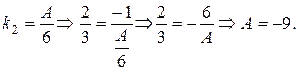
Ответ. а) 4; б) 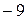
Задача 7 Через точку пересечения прямых  ,
,  проведена прямая, параллельная прямой
проведена прямая, параллельная прямой  .
.
Решение. Найдем точку пересечения прямых  и
и  . Решим систему линейных уравнений
. Решим систему линейных уравнений
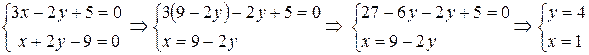
Точка пересечения двух прямых  . Так как прямые параллельны, то нормальные вектора коллинеарны:
. Так как прямые параллельны, то нормальные вектора коллинеарны:  .
.
 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку  с нормальным вектором
с нормальным вектором 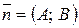 .
.

Ответ. 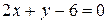
Задача 8 Найти координаты точки  , симметричной точке
, симметричной точке  относительно прямой
относительно прямой  .
.
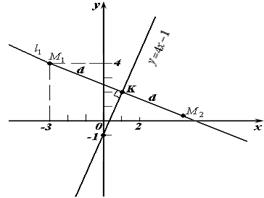
Рисунок 29
Решение. Найдем уравнение прямой  , проходящей через точку
, проходящей через точку  и перпендикулярной данной прямой
и перпендикулярной данной прямой  по формуле
по формуле 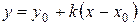 :
: 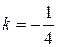 ,
,  .
.
Так как точка  лежит на
лежит на  , то ее координаты удовлетворяют уравнению
, то ее координаты удовлетворяют уравнению  , т.е.
, т.е.  .
.
Найдем расстояние от точки  до прямой
до прямой  .
.
 .
.
Найдем точку пересечения двух прямых:
 .
.
Точка  .
.
Найдем расстояние  , которое равно
, которое равно  :
:
 .
.
Решим систему уравнений:
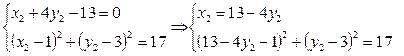
 ,
,
 ,
,

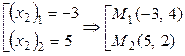
Ответ. 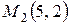
Задача 9 Определить при каком значении  три прямые
три прямые  ,
, 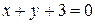 ,
,  будут пересекаться в одной точке.
будут пересекаться в одной точке.
Решение. Для того, чтобы найти при каком значении  три прямые будут пересекаться в одной точке, необходимо решить систему уравнений:
три прямые будут пересекаться в одной точке, необходимо решить систему уравнений:

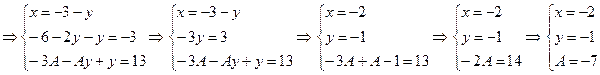
Ответ. 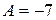
|
|
