Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Расстояние от данной точки до данной прямой

Под углом между прямыми в плоскости понимают наименьший (острый) из двух смежных углов, образованными этими прямыми.

Если прямые и заданы уравнениями с угловыми коэффициентами и , то угол между ними вычисляется по формуле (8)

Рисунок 10

Условие параллельности двух прямых: Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны, т.е.

(9)

Рисунок 11

Условие перпендикулярности двух прямых: Две прямые перпендикулярны тогда и только тогда, когда их угловые коэффициенты противоположны по знаку и обратны по значению, т.е.

(10)

Рисунок 12

Если прямые и заданы общими уравнениями , и , , 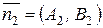то величина угла между ними вычисляется по формулам , . (11)

Рисунок 13

Условие параллельности двух прямых: Две прямые параллельны тогда и только тогда, когда их нормальные вектора коллинеарны, т.е.

( или ) (12)

Рисунок 14

Условие перпендикулярности двух прямых: Две прямые перпендикулярны тогда и только тогда, когда их нормальные вектора перпендикулярны, т.е. ( ) (13)

Рисунок 15

Для нахождения общих точек прямых и необходимо решить систему уравнений

или (14)

При этом:

если 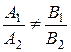, то имеется единственная точка пересечения прямых;

если - прямые и не имеют общей точки, т.е. параллельны;

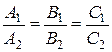если - прямые имеют бесконечное множество общих точек, т.е. совпадают.

Рисунок 16

Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из этой точки на прямую.

Расстояние определяется по формуле

(15)

Расстояние от точки до прямой вычисляется по формуле

(16)

Рисунок 17

Вопросы для самоконтроля

1 Запишите уравнение прямой 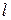, проходящей через две различные точки и .

2 Запишите общее уравнение прямой (изобразите прямую на плоскости). Чем задается прямая заданная общим уравнением?

3 Укажите взаимное расположение двух прямых на плоскости, прямые заданы через угловые коэффициенты.

4 Запишите уравнение прямой 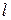проходящей через с угловым коэффициентом .

5 Укажите способы взаимного расположения двух прямых на плоскости, если прямые заданы общими уравнениями.

6 Сформулируйте признаки параллельности и перпендикулярности двух прямых на плоскости.

7 Выведите формулу расстояния от точки до прямой : .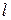

8 Запишите уравнение прямой 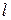, проходящей через точку с направляющим вектором .

9 Выведите нормальное уравнение прямой 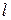. Укажите связь общего уравнение прямой с нормальным уравнением.

10 Запишите параметрическое уравнение прямой на плоскости (изобразите прямую).

11 Выведите уравнение прямой 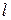, проходящей через с нормальным вектором .

12 Запишите уравнение прямой 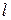с угловым коэффициентом и расстоянием .

13 Запишите уравнение прямой в отрезках (изобразите прямую на плоскости).

14 Дано уравнение Чем задается данная прямая?

15 Дан треугольник АВС. Координаты точек: А (2; -4), В (-2; –1), С (2; 0). Найти уравнение сторон треугольника АВС

16 Дан треугольник АВС. Координаты точек А (2; -4), В (-2; –1), С (2; 0). Найти уравнение медианы ВМ, опущенной из вершины В на сторону АС и уравнение высоты ВК.

17 Составить уравнение прямой 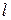, проходящей через точку М (1; 3) и направляющий вектор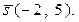

18 Составить уравнение прямой 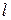, проходящей через точку Р (3; -2) и нормальный вектор .

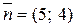19 Найти расстояние от точки А (2; 1) до прямой : .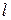

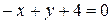20 Даны точки А(2, -1) и В(-3, 4). Найти координаты точки С, которая является серединой отрезка АВ.