Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Основные характеристики детерминированных сигналов.

Детерминированные (или регулярные) сигналы – это сигналы, течение которых во времени можно полностью предопределить.

Заданная аналитически (детерминированная, определенная в любой момент вре- мени), функция s(t) становится абстрактной математической моделью сигнала, не связанной с его физическим характером и удобной для изучения. Примеры математических моделей детерминированных радиотехнических сигналов.

Непрерывный сигнал (гармоническое колебание):

Непрерывный сигнал (гауссов импульс):

Непрерывный сигнал (экспоненциальный импульс):

Финитный сигнал (треугольный видеоимпульс):

Периодический сигнал:

где r (t) — финитный на интервале Т (периоде последовательности) сигнал; ино- гда говорят о «представительном» сигнале последовательности.
Дискретный сигнал, явл яющийся последовательностью отсчетов (чисел):

Тестовые сигналы. Особое место среди математических моделей сигналов занимают модели тестовых, испытате льных или пробных сигналов. Они широко используются в теоретических исследованиях, а приближенно от вечающие им фи- зические (радиотехнические) сигналы — в экспериментальной радиотехнической и радиоизмерительной практике. Известным тестовым сигналом является единичная ступенчатая функция, функция включения, или функция Хевисайда:

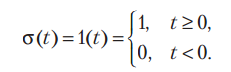
Важнейшим тестов ым радиотехническим сигналом является дельта-функция, или функция Дирака d(t), которая определяется соотношениями

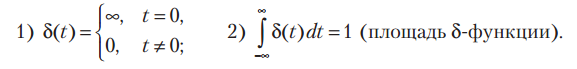
Из первой части определения (1.9) следует, что d(t) существует лишь при аргу- менте t = 0, поэтому справедливо:

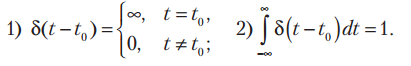
размерность d(t) обратна размерности аргумента t. Отметим также важное соотношение, определяющее фильтрующее свойство d-функции

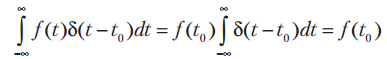
Для анализа сигналов очень важны методы представления математической модели сигнала в виде разложения ее в функциональный ряд. Разложения по линейно не- зависимым и ортогональным системам функций (базисам) широко используются при решении многих задач физики и математики. Бесконечная (в общем случае) система (последовательность) непрерывных на интервале Т функций { () i ϕ t, i = 0, 1, 2, …} является ортогональной на Т, если

где величина

называется нормой системы функций { ()} i ϕ t, при этом никакая из функций системы не равна тождественно нулю (неравенство в соотношении (1.17), определяющем ϕ i). Представление произвольной кусочно-непрерывной модели сигнала s(t), удовлетворяющей условию

в виде линейной комбинации взвешенных функций { () i ϕ t }

называется разложением в обобщенный ряд Фурье. Линейная независимость системы { () i ϕ t } обеспечивает единственность

разложения.

3) АЦП (аналогово-цифровое преобразование) сигналов.
Компьютеры и цифровые устройства могут обрабатывать только дискретные по времени и уровню сигналы, которые называют цифровыми. Для преобразования аналоговых сигналов в цифровые используются специальные устройства – аналого – цифровые преобразователи (АЦП). Аналого – цифровое преобразование (также популярен термин оцифровка сигнала) включает операции дискретизации по времени, квантования по уровню и кодирования значений входного сигнала (см. рис.).

Первичный преобразователь преобразует сообщение в электрическое напряжение, являющееся электрическим аналогом физического сообщения.
Низкочастотная фильтрация – это процесс выделения НЧ компонент сигнала в полосе частот от 0 до Fи подавления его ВЧ компонент на частотах > F.

Дискретизация по времени – это процесс преобразования непрерывного сигнала (НС) в дискретно-непрерывный сигнал (ДНС).
Квантование в АЦП связано с округлением отсчетов до разрешенных уровней.

В процессе квантования образуется специфическая, неустранимая погрешность (шум квантования):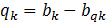

Кодирование – это дискретное отображение элементов одного множества в элементы другого множества по определенному правилу.

Примитивное кодирование связано с представлением чисел в той или иной системе счисления. В современных СПИ часто применяют представление десятичных чисел в двоичной системе счисления.

Сигнал на выходе кодера (Кд) представляется в следующем виде:

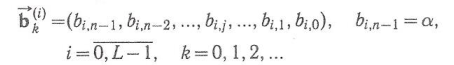
4) Цифро – аналоговое преобразование (ЦАП) сигналов.

Структурная схема ЦАП:

С помощью представленных в схеме процедур ЦАП восстанавливает непрерывный сигнал по его цифровому или дискретно-аналоговому представлениям.

Декодирование – это процесс обратный кодированию, в результате которого осуществляется дискретное отображение элементов одного множества в элементы другого множества по определенному правилу.

Физические значения декодированной посл-ти с учетом шага квантования и знака числа определяются так:

Верхние * в символах означают, что восстанавливаемые символы на приёме могут отличаться от аналогичных символов на передаче из-за ошибок в дискретном канале связи (КС).

Интерполяция – процесс преобразования цифрового сигнала, дискретного по времени, в сигнал, аналоговый по времени. В современных ЦАП используется ступенчатый интерполятор – это линейный фильтр с импульсной характеристикой:

Ступенчатый интерполятор преобразует входные квантованные отсчеты дискретно-аналогового сигнала в последовательность прямоугольных ипульсов длительностью его отклик является ступенчатой аппроксимацией сигнала.

Вторичный преобразователь. Для согласования выхода детектора с входом получателя информации применяют различные устройства её отображения – вторичные преобразователи (динамик, громкоговоритель, принтер и т.д.)

5) Теорема Котельникова имеет фундаментальное значение для дискретного представления аналоговых сигналов и решении многих задач теории связи и техники связи. Формулировка: любая непрерывная функция с ограниченным (фининым) спектром может быть точно представлена своими отсчетами 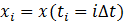, взятыми в момент времени , отстоящими друг от друга на интервал времени (интервал временной дискретизации)

, частота дискретизации:

Согласно выводам данной теоремы, сигнал предсавляется в виде ортогонального ряда Фурье:

Безошибочное представление в любой момент времени сигнала по его отсчетам, взятыми в дискретные моменты времени, возможно только при выполнении следующих ограничений:

· Спектр сигнала строго ограничен верхней частотой

· В восстановлении сигнала участвует бесконечное число отсчетов

· В качестве восстанавливающего устройства используется ИФНЧ

В реальных условиях ни одно из этих условий не выполняется, поэтому восстановление сигнала происходит с некоторой погрешностью.

Временная дискретизация сигналов

Спектр дискретно-аналогового сигнала:

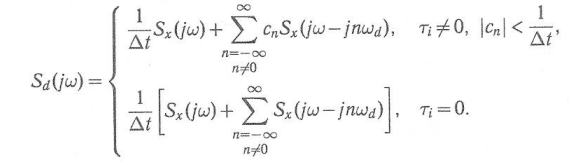
6) Восстановление аналогового (непрерывного) сигнала из отсчётов.

В линию связи передаются импульсы-отсчёты, которые поступают на вход приёмника.

Для восстановления исходного непрерывного сигнала из импульсов-отсчётов надо эти импульсы подать на вход идеального фильтра низких частот (ИФНЧ), который имеет следующие характеристики.

Амплитудно-частотная характеристика идеального ФНЧ (АЧХ ИФНЧ) имеет вид:

K(w)

K

- w_д 0 w_д w

Импульсная реакция ИФНЧ, т.е. реакция на дельта-импульс имеет вид:

g_ифнч (t)

Рис. 3.13

t

-3 Dt - 2Dt -Dt 0 Dt 2Dt 3Dt

(3.6)

Первая формула - это выражение для импульсной реакции ИФНЧ, вторая и третья формулы определяют моменты времени, для которых

g _ИФНЧ(t) обращается в ноль.

Очевидно, что на выходе ИФНЧ получим спектр:

S(w)= K S_д(w) = K S_x(w) /Dt;

или для АИМ сигнала получим: S(w)= KS_д(w) = K a₀S_x(w) /2.

Таким образом, с точностью до постоянного множителя мы получили на выходе ИФНЧ спектр исходного сигнала x(t). С временной точки зрения мы получили исходный непрерывный сигнал x(t).

Погрешности дискретизации и восстановления непрерывных сигналов.

Теорема Котельникова точно справедлива только для сигналов с финитным (конечным) спектром. На рис.3.14 показаны некоторые варианты финитных спектров:

S_x(w) 3

0 w_в w

Рис.3.14.

Однако спектры реальных информационных сигналов бесконечны. В этом случае теорема Котельникова справедлива с погрешностью.

S_x(w)

0 w_в w

Погрешность дискретизации определяется энергией спектральных составляющих сигнала, лежащих за пределами частоты w_в.

(3.7)

Вторая причина возникновения погрешностей - неидеальность восстанавливающего ФНЧ.

Т.о. погрешность дискретизации и восстановления непрерывного сигнала определяется следующими причинами:

1) Спектры реальных сигналов не финитны.

2) АЧХ реальных ФНЧ неидеальны.

Например, если в качестве ФНЧ использовать RC- фильтр, то восстановленный сигнал на его выходе будет иметь вид:

Вывод: чем выше 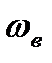и чем ближе характеристики ФНЧ к идеальным, тем ближе восстановленный сигнал к исходному.