Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 21 страница

💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

В отличие от собственной проводимости, осуществляющейся одновременно электронами и дырками, примесная проводимость полупроводников обусловлена в основном носителями одного знака: электронами—в случае донорной примеси, дырками — в случае акцепторной. Эти носители тока называются основными. Кроме основных носителей в полупроводнике имеются и неосновные носители: в полупроводниках n -типа — дырки, в полупроводниках p- типа — электроны.

Наличие примесных уровней в полупроводниках существенно изменяет положение уровня Ферми Е_F. Расчеты показывают, что в случае полупроводников n -типа уровень Ферми Е_F0 при 0 К расположен посередине между дном зоны проводимости и донорным уровнем (рис. 321), С повышением температуры все большее число электронов переходит из донорных состояний в зону проводимости, но, помимо этого, возрастает и число тепловых флуктуаций, способных возбуждать электроны из валентной зоны и перебрасывать их через запрещенную зону энергий. Поэтому при высоких температурах уровень Ферми имеет тенденцию смещаться вниз (сплошная кривая) к своему предельному положению в центре запрещенной зоны, характерному для собственного полупроводника.

Уровень Ферми в полупроводниках р- типа при 0 К Е_F0 располагается посередине между потолком валентной зоны и акцепторным уровнем (рис. 322). Сплошная кривая опять-таки показывает его смещение с температурой. При температурах, при которых примесные атомы оказываются полностью истощенными и увеличение концентрации носителей происходит за счет возбуждения собственных носителей, уровень Ферми располагается посередине запрещенной зоны, как в собственном полупроводнике.

Проводимость примесного полупроводника, как и проводимость любого проводника, определяется концентрацией носителей и их подвижностью. С изменением температуры подвижность носителей меняется по сравнительно слабому степенному закону, а концентрация носителей — по очень сильному экспоненциальному закону, поэтому проводимость примесных полупроводников от температуры определяется в основном температурной зависимостью концентрации носителей тока в нем. На рис. 323 дан примерный график зависимости ln g от 1/ T для примесных полупроводников. Участок AB описывает примесную проводимость полупроводника. Рост примесной проводимости полупроводника с повышением температуры обусловлен в основном ростом концентрации примесных носителей. Участок ВС соответствует области истощения примесей (это подтверждают и эксперименты), участок CD описывает собственную проводимость полупроводника.

Фотопроводимость (см. § 202) полупроводников — увеличение электропроводности полупроводников под действием электромагнитного излучения — может быть связана со свойствами как основного вещества, так и содержащихся в нем примесей. В первом случае при поглощении фотонов, соответствующих собственной полосе поглощения полупроводника, т. е. когда энергия фотонов равна или больше ширины запрещенной зоны (hn ³ D E), могут совершаться перебросы электронов из валентной зоны в зону проводимости (рис. 324, а), что приведет к появлению добавочных (неравновесных) электронов (в зоне проводимости) и дырок (в валентной зоне). В результате возникает собственная фотопроводимость, обусловленная как электронами, так и дырками.

Если полупроводник содержит примеси, то фотопроводимость может возникать и при hn < D E: для полупроводников с донорной примесью фотон должен обладать энергией hn ³ D Е_D, а для полупроводников с акцепторной примесью — hn ³ D Е_A. При поглощении света примесными центрами происходит переход электронов с донорных уровней в зону проводимости в случае полупроводника n -типа (рис. 324, б) или из валентной зоны на акцепторные уровни в случае полупроводника p -типа (рис. 324, в). В результате возникает примесная фотопроводимость, являющаяся чисто электронной для полупроводников п -типа и чисто дырочной для полупроводников p -типа.

(D E _п — в общем случае энергия активации примесных атомов), то в полупроводнике возбуждается фотопроводимость. Из (244.1) можноопределить красную границу фотопроводимости — максимальную длину волны, при которой еще фотопроводимость возбуждается:

Учитывая значения D E и D E _п для конкретных полупроводников, можно показать, что красная граница фотопроводимости для собственных полупроводников приходится на видимую область спектра, для примесных же полупроводников — на инфракрасную.

На рис. 325 представлена типичная зависимость фотопроводимости j и коэффициента поглощения { от длины волны l падающего на полупроводник света. Из рисунка следует, что при l> l ₀ фотопроводимость действительно не возбуждается. Спад фотопроводимости в коротковолновой части полосы поглощения объясняется большой скоростью рекомбинации в условиях сильного поглощения в тонком поверхностном слое толщиной х»1 мкм (коэффициент поглощения»10⁶ м^–1).

Наряду с поглощением, приводящим к появлению фотопроводимости, может иметь место экситонный механизм поглощения. Экситоны представляют собой квазичастицы — электрически нейтральные связанные состояния электрона и дырки, образующиеся в случае возбуждения с энергией, меньшей ширины запрещенной зоны. Уровни энергии экситонов располагаются у дна зоны проводимости. Так как экситоны электрически нейтральны, то их возникновение в полупроводнике не приводит к появлению дополнительных носителей тока, вследствие чего экситонное поглощение света не сопровождается увеличением фотопроводимости.

В природе давно известно излучение, отличное по своему характеру от всех известных видов излучения (теплового излучения, отражения, рассеяния света и т. д.). Этим излучением является люминесцентное излучение, примерами которого может служить свечение тел при облучении их видимым, ультрафиолетовым и рентгеновским излучением, g-излучением и т.д. Вещества, способные под действием различного рода возбуждений светиться, получили название люминофоров.

Люминесценция — неравновесное излучение, избыточное при данной температуре над тепловым излучением тела и имеющее длительность, большую периода световых колебаний. Первая часть этого определения приводит к выводу, что люминесценция не является тепловым излучением (см. § 197), поскольку любое тело при температуре выше 0 К излучает электромагнитные волны, а такое излучение является тепловым. Вторая часть показывает, что люминесценция не является таким видом свечения, как отражение и рассеяние света, тормозное излучение заряженных частиц и т. д. Период световых колебаний составляет примерно 10^–15 с, поэтому длительность, по которой свечение можно отнести к люминесценции, больше—примерно 10^–10 с. Признак длительности свечения дает возможность отличить люминесценцию от других неравновесных процессов. Так, по этому признаку удалось установить, что излучение Вавилова — Черенкова (см. § 189) нельзя отнести к люминесценции.

В зависимости от способов возбуждения различают: фотолюминесценцию (под действием света), рентгенолюминесценцию (под действием рентгеновского излучения), катодолюминесценцию (под действием электронов), электролюминесценцию (под действием электрического поля), радиолюминесценцию (при возбуждении ядерным излучением, например g-излучением, нейтронами, протонами), хемилюминесценцию (при химических превращениях), триболюминесценцию (при растирании и раскалывании некоторых кристаллов, например сахара). По длительности свечения условно различают: флуоресценцию (t £ 10^–8с)и фосфоресценцию — свечение, продолжающееся заметный промежуток времени после прекращения возбуждения.

Первое количественное исследование люминесценции проведено более ста лет назад Дж. Стоксом, * сформулировавшим в 1852 г. следующее правило: длина волны люминесцентного излучения всегда больше длины волны света, возбудившего его (рис. 326). Согласно квантовой теории, правило Стокса означает, что энергия hn падающего фотона частично расходуется на какие-то неоптические процессы, т. е.

откуда n _люм < n или l _люм > l что и следует из сформулированного правила.

* Дж. Стокс (1819—1903) — английский физик и математик.

Основной энергетической характеристикой люминесценции является энергетический выход, введенный С. И. Вавиловым в 1924 г., — отношение энергии, излученной люминофором при полном высвечивании, к энергии, поглощенной им. Типичная для органических люминофоров (на примере раствора флуоресцина) зависимость энергетического выхода h от длины волны l возбуждающего света представлена на рис. 327. Из рисунка следует, что вначале h растет пропорционально l, а затем, достигая максимального значения, быстро спадает до нуля при дальнейшем увеличении l (закон Вавилова). Величина энергетического выхода для различных люминофоров колеблется в довольно широких пределах, максимальное ее значение может достигать примерно 80%.

Твердые тела, представляющие собой эффективно люминесцирующие искусственно приготовленные кристаллы с чужеродными примесями, получили название кристаллофосфоров. На примере кристаллофосфоров рассмотрим механизмы возникновения люминесценции с точки зрения зонной теории твердых тел. Между валентной зоной и зоной проводимости кристаллофосфора располагаются примесные уровни активатора (рис. 328). При поглощении атомом активатора фотона с энергией hn электрон с примесного уровня переводится в зону проводимости, свободно перемещается по кристаллу до тех пор, пока не встретится с ионом активатора и не рекомбинирует с ним, перейдя вновь на примесный уровень. Рекомбинация сопровождается излучением кванта люминесцентного свечения. Время высвечивания люминофора определяется временем жизни возбужденного состояния атомов активатора, которое обычно не превышает миллиардных долей секунды. Поэтому свечение является кратковременным и исчезает почти вслед за прекращением облучения.

Для возникновения длительного свечения (фосфоресценции) кристаллофосфор должен содержать также центры захвата, или ловушки для электронов, представляющие собой незаполненные локальные уровни (например, Л₁ и Л₂), лежащие вблизи дна зоны проводимости (рис. 329). Они могут быть образованы атомами примесей, атомами в междоузлиях и т. д. Под действием света атомы активатора возбуждаются, т. е. электроны с примесного уровня переходят в зону проводимости и становятся свободными. Однако они захватываются ловушками, в результате чего теряют свою подвижность, а следовательно, и способность рекомбинировать с ионом активатора. Освобождение электрона из ловушки требует затраты определенной энергии, которую электроны могут получить, например, от тепловых колебаний решетки. Освобожденный из ловушки электрон попадает в зону проводимости и движется по кристаллу до тех пор, пока или не будет снова захвачен ловушкой, или не рекомбинирует с ионом активатора. В последнем случае возникает квант люминесцентного излучения. Длительность этого процесса определяется временем пребывания электронов в ловушках.

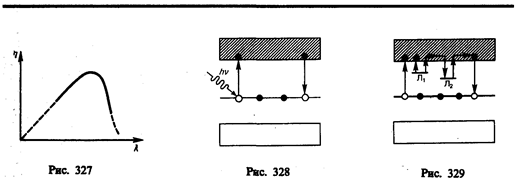
Явление люминесценции получило широкое применение в практике, например люминесцентный анализ — метод определения состава вещества по характерному его свечению. Этот метод, являясь весьма чувствительным (примерно 10^–10 г / см³), позволяет обнаруживать наличие ничтожных примесей и применяется при тончайших исследованиях в биологии, медицине, пищевой промышленностии т. д. Люминесцентная дефектоскопия позволяет обнаружить тончайшие трещины на поверхности деталей машин и других изделий (исследуемая поверхность покрывается для этого люминесцентным раствором, который после удаления остается в трещинах).

Люминофоры используются в люминесцентных лампах, являются активной средой оптических квантовых генераторов (см. § 233) и сцинтилляторов (будут рассмотрены ниже), применяются в электронно-оптических преобразователях (см. § 169), для создания аварийного и маскировочного освещения и для изготовления светящихся указателей различных приборов.

Если два различных металла привести в соприкосновение, то между ними возникает разность потенциалов, называемая контактной разностью потенциалов. Итальянский физик А. Вольта (1745—1827) установил, что если металлы А1, Zn, Sn, Pb, Sb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd привести в контакт в указанной последовательности, то каждый предыдущий при соприкосновении с одним из следующих зарядится положительно. Этот ряд называется рядом Вольта. Контактная разность потенциалов для различных металлов составляет от десятых до целых вольт.

Вольта экспериментально установил два закона:

1. Контактная разность потенциалов зависит лишь от химического состава и температуры соприкасающихся металлов.

2. Контактная разность потенциалов последовательно соединенных различных проводников, находящихся при одинаковой температуре, не зависит от химического состава промежуточных проводников и равна контактной разности потенциалов, возникающей при непосредственном соединении крайних проводников.

Для объяснения возникновения контактной разности потенциалов воспользуемся представлениями зонной теории. Рассмотрим контакт двух металлов с различными работами выхода А ₁ и А ₂, т.е. с различными положениями уровня Ферми (верхнего заполненного электронами энергетического уровня). Если A ₁ < A ₂ (этот случай изображен на рис. 330, а), то уровень Ферми располагается в металле 1 выше, чем в металле 2. Следовательно, при контакте металлов электроны с более высоких уровней металла 1 будут переходить на более низкие уровни металла 2, что приведет к тому, что металл 1 зарядится положительно, а металл 2 — отрицательно. Одновременно происходит относительное смещение энергетических уровней: в металле, заряжающемся положительно, все уровни смещаются вниз, а в металле, заряжающемся отрицательно, — вверх. Этот процесс будет происходить до тех пор, пока между соприкасающимися металлами не установится равновесие, которое, как доказывается в статистической физике, характеризуется совпадением уровней Ферми в обоих металлах (рис. 330, б).

Так как для соприкасающихся металлов уровни Ферми совпадают, а работы выхода А ₁ и A ₂ не изменяются (они являются константами металлов и не зависят от того, находятся металлы в контакте или нет), то потенциальная энергия электронов в точках, лежащих вне металлов в непосредственной близости к их поверхности (точки А и В на рис. 330, б), будет различной. Следовательно, между точками А и В устанавливается разность потенциалов, которая, как следует из рисунка, равна

Разность потенциалов (246.1), обусловленная различием работ выхода контактирующих металлов, называется внешней контактной разностью потенциалов. Чаще говорят просто о контактной разности потенциалов, подразумевая под ней внешнюю.

Если уровни Ферми для двух контактирующих металлов не одинаковы, то между внутренними точками металлов наблюдается внутренняя контактная разность потенциалов, которая, как следует из рисунка, равна

В квантовой теории доказывается, что причиной возникновения внутренней контактной разности потенциалов является различие концентраций электронов в контактирующих металлах. D j '' зависит от температуры T контакта металлов (поскольку наблюдается зависимость Е_F от T), обусловливая термоэлектрические явления. Как правило, D j ''< < D j '.

Если, например, привести в соприкосновение три разнородных проводника, имеющих одинаковую температуру, то разность потенциалов между концами разомкнутой цепи равна алгебраической сумме скачков потенциала во всех контактах. Она, как можно показать (предоставляем это сделать читателю), не зависит от природы промежуточных проводников (второй закон Вольта).

Внутренняя контактная разность потенциалов возникает в двойном электрическом слое, образующемся в приконтактной области и называемом контактным слоем. Толщина контактного слоя в металлах составляет примерно 10^–10 м, т. е. соизмерима с междоузельными расстояниями в решетке металла. Число электронов, участвующих в диффузии через контактный спой, составляет примерно 2% от общего числа электронов, находящихся на поверхности металла. Столь незначительное изменение концентрации электронов в контактном слое, с одной стороны, и малая по сравнению с длиной свободного пробега электрона его толщина — с другой, не могут привести к заметному изменению проводимости контактного слоя по сравнению с остальной частью металла. Следовательно, электрический ток через контакт двух металлов проходит так же легко, как и через сами металлы, т.е. контактный слой проводит электрический ток в обоих направлениях (1 ® 2 и 2 ® 1) одинаково и не дает эффекта выпрямления, который всегда связан с односторонней проводимостью.

§ 247. Термоэлектрические явления и их применение

Согласно второму закону Вольта, в замкнутой цепи, состоящей из нескольких металлов, находящихся при одинаковой температуре, э.д.с. не возникает, т. е. не происходит возбуждения электрического тока. Однако если температура контактов не одинакова, то в цепи возникает электрический ток, называемый термоэлектрическим. Явление возбуждения термоэлектрического тока (явление Зеебека), а также тесно связанные с ним явления Пельте и Томсона называются термоэлектрическими явлениями.0

1. Явление Зеебека (1821). Немецкий физик Т. Зеебек (1770—1831) обнаружил, что в замкнутой цепи, состоящей из последовательно соединенных разнородных проводников, контакты между которыми имеют различную температуру, возникает электрический ток.

Рассмотрим замкнутую цепь, состоящую из двух металлических проводников 1 и 2 с температурами спаев Т ₁ (контакт А) и Т ₂ (контакт В), причем Т ₁ > T ₂ (рис. 331).

Не вдаваясь в подробности, отметим, что в замкнутой цепи для многих пар металлов (например, Сu—Bi, Ag—Сu, Аu—Сu) электродвижущая сила прямо пропорциональна разности температур в контактах:

Эта э.д.с. называется термоэлектродвижущей силой. Направление тока при Т ₁ > Т ₂ на рис. 331 показано стрелкой. Термоэлектродвижущая сила, например для пары металлов медь — константан, для разности температур 100 К составляет всего 4, 25 мВ.

Причина возникновения термоэлектродвижущей э.д.с. ясна уже из формулы (246.2), определяющей внутреннюю контактную разность потенциалов на границе двух металлов. Дело в том, что положение уровня Ферми зависит от температуры. Поэтому если температуры контактов разные, то разными будут и внутренние контактные разности потенциалов. Таким образом, сумма скачков потенциала отлична от нуля, что и приводит к возникновению термоэлектрического тока. Отметим также, что при градиенте температуры происходит и диффузия электронов, которая тоже обусловливает термо-э.д.с.

Явление Зеебека не противоречит второму началу термодинамики, таккак в данном случае внутренняя энергия преобразуется в электрическую, для чего используется два источника теплоты (два контакта). Следовательно, для поддержания постоянного тока в рассматриваемой цепи необходимо поддерживать постоянство разности температур контактов: к более нагретому контакту непрерывно подводить теплоту, а от холодного — непрерывно ее отводить.

Явление Зеебека используется для измерения температуры. Для этого применяются термоэлементы, или термопары —датчики температур, состоящие из двух соединенных между собой разнородных металлических проводников. Если контакты (обычно спаи) проводников (проволок), образующих термопару, находятся при разных температурах, то в цепи возникает термоэлектродвижущая сила, которая зависит от разности температур контактов и природы применяемых материалов. Чувствительность термопар выше, если их соединять последовательно. Эти соединения называются термобатареями (или термостолбиками). Термопары применяются как для измерения ничтожно малых разностей температур, так и для измерения очень высоких и очень низких температур (например, внутри доменных печей или жидких газов). Точность определения температуры с помощью термопар составляет, как правило, несколько кельвин, а у некоторых термопар достигает»0, 01 К. Термопары обладают рядом преимуществ перед обычными термометрами: имеют большую чувствительность и малую инерционность, позволяют проводить измерения в широком интервале температур и допускают дистанционные измерения.

Явление Зеебека в принципе может быть использовано для генерации электрического тока. Так, уже сейчас к.п.д. полупроводниковых термобатарей достигает»18%. Следовательно, совершенствуя полупроводниковые термоэлектрогенераторы, можно добиться эффективного прямого преобразования солнечной энергии в электрическую.

2. Явление Пельтье (1834). Французский физик Ж. Пельтье (1785—1845) обнаружил, что при прохождении через контакт двух различных проводников электрического тока в зависимости от его направления помимо джоулевой теплоты выделяется или поглощается дополнительная теплота. Таким образом, явление Пельтье является обратным по отношению к явлению Зеебека. В отличие от джоулевой теплоты, которая пропорциональна квадрату силы тока, теплота Пельтье пропорциональна первой степени силы тока и меняет знак при изменении направления тока.

Рассмотрим замкнутую цепь, состоящую из двух разнородных металлических проводников 1 и 2 (рис. 332), по которым пропускается ток I ' (его направление в данном случае выбрано совпадающим с направлением термотока (на рис. 331 при условии T ₁ > T ₂)). Согласно наблюдениям Пельтье, спай А, который при явлении Зеебека поддерживался бы при более высокой температуре, будет теперь охлаждаться, а спай В — нагреваться. При изменении направления тока I ' спай А будет нагреваться, спай В — охлаждаться.

Объяснить явление Пельтье можно следующим образом. Электроны по разную сторону спая обладают различной средней энергией (полной—кинетической плюс потенциальной). Если электроны (направление их движения задано на рис. 332 пунктирными стрелками) пройдут через спай В и попадут в область с меньшей энергией, то избыток своей энергии они отдадут кристаллической решетке и спай будет нагреваться. В спае А электроны переходят в область с большей энергией, забирая теперь недостающую энергию у кристаллической решетки, и спай будет охлаждаться.

Явление Пельтье используется в термоэлектрических полупроводниковых холодильниках, созданных впервые в 1954 г. под руководством А. Ф. Иоффе, и в некоторых электронных приборах.

3. Явление Томсона (1856). Вильям Томсон (Кельвин), исследуя термоэлектрические явления, пришел к заключению, подтвердив его экспериментально, что при прохождении тока по неравномерно нагретому проводнику должно происходить дополнительное выделение (поглощение) теплоты, аналогичной теплоте Пельтье. Это явление получило название явления Томсона. Его можно объяснить следующим образом. Так как в более нагретой части проводника электроны имеют большую среднюю энергию, чем в менее нагретой, то, двигаясь в направлении убывания температуры, они отдают часть своей энергии решетке, в результате чего происходит выделение теплоты Томсона. Если же электроны движутся в сторону возрастания температуры, то они, наоборот, пополняют свою энергию за счет энергии решетки, в результате чего происходит поглощение теплоты Томсона.

§ 248. Выпрямление на контакте металл — полупроводник

Рассмотрим некоторые особенности механизма процессов, происходящих при приведении в контакт металла с полупроводником. Для этого возьмем полупроводник л-типа с работой выхода А, меньшей работы выхода А _м из металла. Соответствующие энергетические диаграммы до и после приведения в контакт показаны на рис. 333, а, б.

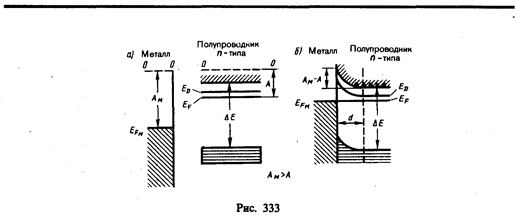
Если А _м > А, то при контакте электроны из полупроводника будут переходить в металл, в результате чего контактный слой полупроводника обеднится электронами и зарядится положительно, а металл — отрицательно. Этот процесс будет происходить до достижения равновесного состояния, характеризуемого, как и при контакте двух металлов, выравниванием уровней Ферми для металла и полупроводника. На контакте образуется двойной электрический слой d, поле которого (контактная разность потенциалов) препятствует дальнейшему переходу электронов. Вследствие малой концентрации электронов проводимости в полупроводнике (порядка 10¹⁵ см^–3 вместо 10²¹ см^–3 в металлах) толщина контактного слоя в полупроводнике достигает примерно 10^–6 см, т. е. примерно в 10 000 раз больше, чем в металле. Контактный спой полупроводника обеднен основными носителями тока — электронами в зоне проводимости, и его сопротивление значительно больше, чем в остальном объеме полупроводника. Такой контактный слой называется запирающим.

При d= 10^–6 см и D j»1 В напряженность электрического поля контактного слоя E= D j/d» 10⁸ В/м. Такое контактное поле не может сильно повлиять на структуру спектра (например, на ширину запрещенной зоны, на энергию активации примесей и т. д.) и его действие сводится лишь к параллельному искривлению всех энергетических уровней полупроводника в области контакта (рис. 333, б). Так как в случае контакта уровни Ферми выравниваются, а работы выхода—величины постоянные, то при А _м > А энергия электронов в контактном слое полупроводника больше, чем в остальном объеме. Поэтому в контактном слое дно зоны проводимости поднимается вверх, удаляясь от уровня Ферми. Соответственно происходит и искривление верхнего края валентной зоны, а также донорного уровня.

Помимо рассмотренного выше примера возможны еще следующие три случая контакта металла с примесными полупроводниками: a) А _м < А, полупроводник п -типа; б) А _м > А, полупроводник p -типа; в) А _м < А, полупроводник р -типа. Соответствующие зонные схемы показаны на рис. 334.

Если А _м < А, то при контакте металла с полупроводником п -типа электроны из металла переходят в полупроводник и образуют в контактном слое полупроводника отрицательный объемный заряд (рис. 334, а). Следовательно, контактный слой полупроводника обладает повышенной проводимостью, т.е. не является запирающим. Рассуждая аналогично, можно показать, что искривление энергетических уровней по сравнению с контактом металл — полупроводник п -типа (А _м > А) происходит в обратную сторону.

При контакте металла с полупроводником р -типа запирающий слой образуется при А _м < А (рис. 334, в), так как в контактном слое полупроводника наблюдается избыток отрицательных ионов акцепторных примесей и недостаток основных носителей тока—дырок в валентной зоне. Если же А _м > А (рис. 334, б), то в контактном слое полупроводника р- типа наблюдается избыток основных носителей тока — дырок в валентной зоне, контактный слой обладает повышенной проводимостью.