
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 19 страница
|
|
Для выделения направления лазерной генерации используется принципиально важный элемент лазера — оптический резонатор. В простейшем случае им служит пара обращенных друг к другу параллельных (или вогнутых) зеркал на общей оптической оси, между которыми помещается активная среда (кристалл или кювета с газом). Как правило, зеркала изготовляются так, что от одного из них излучение полностью отражается, а второе — полупрозрачно. Фотоны, движущиеся под углами к оси кристалла или кюветы, выходят из активной среды через ее боковую поверхность. Те же из фотонов, которые движутся вдоль оси, многократно отразятся от противоположных торцов, каждый раз вызывая вынужденное испускание вторичных фотонов, которые, в свою очередь, вызовут вынужденное излучение, и т. д. Так как фотоны, возникшие при вынужденном излучении, движутся в том же направлении, что и первичные, то поток фотонов, параллельный оси кристалла или кюветы, будет лавинообразно нарастать. Многократно усиленный поток фотонов выходит через полупрозрачное зеркало, создавая строго направленный световой пучок огромной яркости. Таким образом, оптический резонатор «выясняет» направление (вдоль оси) усаливаемого фотонного потока, формируя тем самым лазерное излучение с высокими когерентными свойствами. Первым газовым лазером непрерывного действия (1961) был лазер на смеси атомов неона и гелия. Газы обладают узкими линиями поглощения, лампы же излучают свет в широком интервале длин волн; следовательно, применять их в качестве накачки невыгодно, так какиспользуется только часть мощности лампы. Поэтому в газовых лазерах инверсная населенность уровней осуществляется электрическим разрядом, возбуждаемым в газах.
В гелий-неоновом лазере накачка происходит в два этапа: гелий служит носителем энергии возбуждения, а неон дает лазерное излучение. Электроны, образующиеся в разряде, при столкновениях возбуждают атомы гелия, которые переходят в возбужденное состояние 3 (рис. 311). При столкновениях возбужденных атомов гелия с атомами неона происходит их возбуждение и они переходят на один из верхних уровней неона, который расположен вблизи соответствующего уровня гелия. Переход атома неона с верхнего уровня 3 на один из нижних уровней 2 приводит к лазерному излучению с l=0, 6328 мкм.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение

Лазерное излучение обладает следующими свойствами:
1. Временная и пространственная когерентность (см. § 171). Время когерентности составляет 10–3 с, что соответствует длине когерентности порядка 105 м (l ког = сt ког), т. е. на семь порядков выше, чем для обычных источников света.
2. Строгая монохроматичность (D l< 10–11 м).
3. Большая плотность потока энергии. Если, например, рубиновый стержень при накачке получил энергию W= 20 Дж и высветился за 10–3 с, то поток излучения Ф е =20/10–3 Дж/с=2× 104 Вт. Фокусируя это излучение на площади 1 мм2, получим плотность потока энергии Ф е/S = 2× 104/10–6 Вт/м2 = 2× 1010 Вт/м2.
4. Очень малое угловое расхождение в пучке. Например, при использовании специальной фокусировки луч лазера, направленный с Земли, дал бы на поверхности Луны световое пятно диаметром примерно 3 км (луч прожектора осветил бы поверхность диаметром примерно 40 000 км).
К.п.д. лазеров колеблется в широких пределах — от 0, 01% (для гелий-неонового лазера) до 75% (для лазера на стекле с неодимом), хотя у большинства лазеров к.п.д. составляет 0, 1—1%. Создан мощный СО2-лазер непрерывного действия, генерирующий инфракрасное излучение (l=10, 6 мкм), к.п.д. которого (30%) превосходит к.п.д. существующих лазеров, работающих при комнатной температуре.
Необычные свойства лазерного излучения находят в настоящее время широкое применение.
Применение лазеров для обработки, резания и микросварки твердых материалов оказывается экономически более выгодным (например, пробивание калиброванных отверстий в алмазе лазерным лучом сократило время с 24 ч до 6—8 мин). Лазеры применяются для скоростного и точного обнаружения дефектов в изделиях, для тончайших операций (например, луч СО2-лазера в качестве бескровного хирургического ножа), для исследования механизма химических реакций и влияния на их ход, для получения сверхчистых веществ. Широко применяется лазерное разделение изотопов, например такого важного в энергетическом отношении элемента, как уран.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Одним из важных применений лазеров является получение и исследование высокотемпературной плазмы. Эта область их применения связана с развитием нового направления — лазерного управляемого термоядерного синтеза.
Лазеры широко применяются в измерительной технике. Лазерные интерферометры (в них источником света служит лазер) используются для сверхточных дистанционных измерений линейных перемещений, коэффициентов преломления среды, давления, температуры. Например, рассмотренный выше гелий-неоновый лазер из-за излучения высокой стабильности, направленности и монохроматичности (полоса частот 1 Гц при частоте 1014 Гц) незаменим при юстировочных и нивелировочных работах.
Интересное применение лазеры нашли в топографии (см. § 184). Для создания систем голографической памяти с высокой степенью считывания и большой емкостью необходимы газовые лазеры видимого диапазона еще более высокой монохроматичности и направленности излучения.
Очень перспективны и интересны полупроводниковые лазеры, так как они обладают широким рабочим диапазоном (0, 7—30 мкм) и возможностью плавной перестройки частоты их излучения.
Применения лазеров в настоящее время столь обширны, что даже их перечисление в объеме настоящего курса просто невозможно.
Глава 30Элементы квантовой статистики
§ 234. Квантовая статистика. Фазовое пространство. Функция распределения
Квантовая статистика — раздал статистической физики, исследующий системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.
В отличие от исходных положений классической статистической физики, в которой тождественные частицы различимы (частицу можно отличить от всех таких же частиц), квантовая статистика основывается на принципе неразличимости тождественных частиц (см. § 226). При этом оказывается, как будет показано ниже, что коллективы частиц с целым и полуцелым спинами подчиняются разным статистикам.
Пусть система состоит из N частиц. Введем в рассмотрение многомерное пространство всех координат и импульсов частиц системы. Тогда состояние системы определяется заданием 6 N переменных, так как состояние каждой частицы определяется тройкой координат х, у, z и тройкой соответствующих проекций импульса рх, ру, pz. Соответственно число «взаимно перпендикулярных» координатных осей данного пространства равно 6 N. Это 6 N -мерное пространство называется фазовым пространством. Каждому микросостоянию системы отвечает точка в 6 N -мерном фазовом пространстве, так как задание точки фазового пространства означает задание координат и импульсов всех частиц системы. Разобьем фазовое пространство на малые 6 N -мерные элементарные ячейки объемом dqdp=dq 1 dq 2 ...dq 3 N dp 1 dp 2 ...dp 3 N , где q — совокупность координат всех частиц, р — совокупность проекций их импульсов. Корпускулярно-волновой дуализм свойств вещества (см. § 213) и соотношение неопределенностей Гейзенберга (см. § 215) приводят к выводу, что объем элементарной ячейки (он называется фазовым объемом) не может быть меньше чем h 3(h — постоянная Планка).
Вероятность d W данного состояния системы можно представить с помощью функции распределения f (q, p):
 (234.1)
(234.1)
Здесь dW— вероятность того, что точка фазового пространства попадет в элемент фазового объема d q d p, расположенного вблизи данной точки q, р. Иными словами, dW представляет собой вероятность того, что система находится в состоянии, в котором ее координаты и импульсы, заключены в интервале q, q+dq и р, p+dp.
Согласно формуле (234.1), функция распределения есть не что иное, как плотность вероятности определенного состояния системы. Поэтому она должна быть нормирована на единицу:
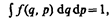
где интегрирование производится по всему фазовому пространству.
Зная функцию распределения f(q, р), можно решить основную задачу квантовой статистики — определить средние значения величин, характеризующих рассматриваемую систему. Среднее значение любой функции
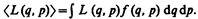 (234.2)
(234.2)
Если иметь дело не с координатами и импульсами, а с энергией, которая квантуется, то состояние системы характеризуется не непрерывной, а дискретной функцией распределения.
Явное выражение функции распределения в самом общем виде получил американский физик Д. Гиббс (1839—1903). Оно называется каноническим распределением Гиббса. В квантовой статистике каноническое распределение Гиббса имеет вид
 (234.3)
(234.3)
где А — постоянная, определяемая из условия нормировки к единице, n — совокупность всех квантовых чисел, характеризующих данное состояние. Подчеркнем, что f (Еn) есть именно вероятность данного состояния, а не вероятность того, что система имеет определенное значение энергии Еn, таккак данной энергии может соответствовать не одно, а несколько различных состояний (может иметь место вырождение).
§ 235. Понятие о квантовой статистике Бозе — Эйнштейна и Ферми — Дирака
Одним из важнейших «объектов» изучения квантовой статистики, как и классической, является идеальный газ. Это связано с тем, что во многих случаях реальную систему можно в хорошем приближении считать идеальным газом. Состояние системы невзаимодействующих частиц задается с помощью так называемых чисел заполнения Ni — чисел, указывающих степень заполнения квантового состояния (характеризуется данным набором i квантовых чисел) частицами системы, состоящей из многих тождественных частиц. Для систем частиц, образованных бозонами — частицами с нулевым или целым спином (см. § 226), числа заполнения могут принимать любые целые значения: 0, 1, 2,... (см. § 227). Для систем частиц, образованных фермионами — частицами с полуцелым спином (см. § 226), числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых (см. § 227). Сумма всех чисел заполнения должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т. е. определить средние числа заполнения á Ni ñ.
Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе — Эйнштейна. * Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым (см. § 227):
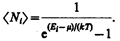 (235.1)
(235.1)
* Ш. Бозе (1894—1974) — индийский физик.
Это распределение называется распределением Бозе — Эйнштейна. Здесь á Ni ñ — среднее число бозонов в квантовом состоянии с энергией Ei, k — постоянная Больцмана, Т— термодинамическая температура, m —химический потенциал; m не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал находится обычно из условия, что сумма всех á Ni ñ равна полному числу частиц в системе. Здесь m £ 0, так как иначе среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фиксированы.
Идеальный газ из фермионов — ферми-газ — описывается квантовой статистикой Ферми — Дирака. * Распределение фермионов по энергиям имеет вид
 (235.2)
(235.2)
где á Ni ñ — среднее число фермионов в квантовом состоянии с энергией Еi, m — химический потенциал. В отличие от (235.1) m может иметь положительное значение (это не приводит к отрицательным значениям чисел á Ni ñ). Это распределение называется распределением Ферми — Дирака.
* Э. Ферми (1901—1954) — итальянский физик.
Если  > > 1, то распределения Бозе — Эйнштейна (235.1) и Ферми — Дирака (235.2) переходят в классическое распределение Максвелла — Больцмана:
> > 1, то распределения Бозе — Эйнштейна (235.1) и Ферми — Дирака (235.2) переходят в классическое распределение Максвелла — Больцмана:
 (235.3)
(235.3)
(ср. с выражением (44.4)), где
 (235.4)
(235.4)
Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.
Система частиц называется вырожденной, если ее свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Поведение как бозе-газа, так и ферми-газа отличается от классического газа, они являются вырожденными газами. Вырождение газов становится существенным при весьма низких температурах и больших плотностях. Параметром вырождения называется величина А. При А < < 1, т. е. при малой степени вырождения, распределения Бозе — Эйнштейна (235.1) и Ферми — Дирака (235.2) переходят в классическое распределение Максвелла — Больцмана (235.3).
Температурой вырождения Т 0 называется температура, ниже которой отчетливо проявляются квантовые свойства идеального газа, обусловленные тождественностью частиц, т. е. Т 0 — температура, при которой вырождение становится существенным. Если Т > > Т 0, то поведение системы частиц (газа) описывается классическими законами.
§ 236. Вырожденный электронный газ в металлах
Распределение электронов по различным квантовым состояниям подчиняется принципу Паули (см. § 227), согласно которому в одном состоянии не может быть двух одинаковых (с одинаковым набором четырех квантовых чисел) электронов, они должны отличаться какой-то характеристикой, например направлением спина. Следовательно, по квантовой теории, электроны в металле не могут располагаться на самом низшем энергетическом уровне даже при 0 К. Согласно принципу Паули, электроны вынуждены взбираться вверх «по энергетической лестнице».
Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми — Дирака (235.2). Если m 0 — химический потенциал электронного газа при Т= 0 К, то, согласно (235.2), среднее число á N (E)ñ электронов в квантовом состоянии с энергией Е равно
 (236.1)
(236.1)
Для фермионов (электроны являются фермионами) среднее число частиц в квантовом состоянии и вероятность заселенности квантового состояния совпадают, так как квантовое состояние либо может быть не заселено, либо в нем будет находиться одна частица. Это означает, что для фермионов á N (E)ñ =f(E), где f(E) — функция распределения электронов по состояниям.
Из (236.1) следует, что при T =0 К функция распределения á N (E)ñ = 1, если E< m 0, и á N (E)ñ = 0, если Е> m 0. График этой функции приведен на рис. 312, а. В области энергий от 0 до m 0 функция á N (E)ñ равна единице. При E=m 0 она скачкообразно изменяется до нуля. Это означает, что при Т= 0К все нижние квантовые состояния, вплоть до состояния с энергией E=m 0, заполнены электронами, а все состояния с энергией, большей m 0, свободны. Следовательно, m 0 есть не что иное, как максимальная кинетическая энергия, которую могут иметь электроны проводимости в металле при 0 К. Эта максимальная кинетическая энергия называется энергией Ферми и обозначается ЕF (ЕF=m 0). Поэтому распределение Ферми — Дирака обычно записывается в виде
 (236.2)
(236.2)
Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми. Уровню Ферми соответствует энергия Ферми ЕF, которую имеют электроны на этом уровне. Уровень Ферми, очевидно, будет тем выше, чем больше плотность электронного газа. Работу выхода электрона из металла нужно отсчитывать не от дна «потенциальной ямы», как это делалось в классической теории, а от уровня Ферми, т. е. от верхнего из занятых электронами энергетических уровней.
Для металлов при не слишком высоких температурах выполняется неравенство kT< < EF. Это означает, что электронный газ в металлах практически всегда находится в состоянии сильного вырождения. Температура Т 0 вырождения (см. § 235) находится из условия kT 0 =EF. Она определяет границу, выше которой квантовые эффекты перестают быть существенными. Соответствующие расчеты показывают, что для электронов в металле T 0»104 К, т. с. для всех температур, при которых металл может существовать в твердом состоянии, электронный газ в металле вырожден.
При температурах, отличных от 0 К, функция распределения Ферми — Дирака (236.2) плавно изменяется от 1 до 0 в узкой области (порядка kT) в окрестности ЕF (рис. 312, б). (Здесь же для сравнения пунктиром приведена функция распределения при T =0 К.) Это объясняется тем, что при T > 0 небольшое число электронов с энергией, близкой к ЕF, возбуждается вследствие теплового движения и их энергия становится больше ЕF. Вблизи границы Ферми при Е< ЕF заполнение электронами меньше единицы, а при Е> ЕF — больше нуля. В тепловом движении участвует лишь небольшое число электронов, например при комнатной температуре Т»300 К и температуре вырождения T 0=3× 104 К, — это 10–5 от общего числа электронов.

Если (Е–ЕF)> > kТ («хвост» функции распределения), то единицей в знаменателе (236.2) можно пренебречь по сравнению с экспонентой и тогда распределение Ферми — Дирака переходит в распределение Максвелла — Больцмана. Таким образом, при (Е–ЕF)> > kT, т.е. при больших значениях энергии, к электронам в металле применима классическая статистика, в то же время, когда (Е–ЕF)< < kT, к ним применима только квантовая статистика Ферми — Дирака.
§ 237. Понятие о квантовой теории теплоемкости. Фононы
Квантовая статистика устранила трудности в объяснении зависимости теплоемкости газов (в частности, двухатомных) от температуры (см. § 53). Согласно квантовой механике, энергия вращательного движения молекул и энергия колебаний атомов в молекуле могут принимать лишь дискретные значения. Если энергия теплового движения значительно меньше разности энергий соседних уровней энергии (kT < < D E), то при столкновении молекул вращательные и колебательные степени свободы практически не возбуждаются. Поэтому при низких температурах поведение двухатомного газа подобно одноатомному.
Так как разность между соседними вращательными уровнями энергии значительно меньше, чем между колебательными, т. е. D E вращ< < D E кол (см. § 230), то с ростом температуры возбуждаются вначале вращательные степени свободы, в результате чего теплоемкость возрастает; при дальнейшем росте температуры возбуждаются и колебательные степени свободы и происходит дальнейший рост теплоемкости (см. рис. 80).
Функции распределения Ферми — Дирака для T =0 К и T > 0 заметно различаются (рис. 312) лишь в узкой области энергий (порядка kT). Следовательно, в процессе нагревания металла участвует лишь незначительная часть всех электронов проводимости.Этим и объясняется отсутствие заметной разницы между теплоемкостями металлов и диэлектриков, что не могло быть объяснено классической теорией (см. § 103).
Как уже указывалось (см. § 73), классическая теория не смогла объяснить также зависимость теплоемкости твердых тел от температуры, а квантовая статистика решила эту задачу. Так, А. Эйнштейн, приближенно считая, что колебания атомов кристаллической решетки независимы (модель кристалла как совокупности независимых колеблющихся с одинаковой частотой гармонических осцилляторов), создал качественную квантовую теорию теплоемкости кристаллической решетки. Она впоследствии была развита П. Дебаем, который учел, что колебания атомов в кристаллической решетке не являются независимыми (рассмотрел непрерывный спектр частот гармонических осцилляторов).
Рассматривая непрерывный спектр частот осцилляторов, П. Дебай показал, что основной вклад в среднюю энергию квантового осциллятора вносят колебания низких частот, соответствующих упругим волнам. Поэтому тепловое возбуждение твердого тела можно описать в виде упругих волн, распространяющихся в кристалле. Согласно корпускулярно-волновому дуализму свойств вещества, упругим волнам в кристалле сопоставляют фононы, обладающие энергией Е= 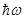 . Фонон есть квант энергии звуковой волны (так как упругие волны — волны звуковые). Фононы являются квазичастицами — элементарными возбуждениями, ведущими себя подобно микрочастицам. Аналогично тому как квантование электромагнитного излучения привело к представлению о фотонах, квантование упругих волн привело к представлению о фононах.
. Фонон есть квант энергии звуковой волны (так как упругие волны — волны звуковые). Фононы являются квазичастицами — элементарными возбуждениями, ведущими себя подобно микрочастицам. Аналогично тому как квантование электромагнитного излучения привело к представлению о фотонах, квантование упругих волн привело к представлению о фононах.
Квазичастицы, в частности фононы, сильно отличаются от обычных частиц (например, электронов, протонов, фотонов), так как они связаны с коллективным движением многих частиц системы. Квазичастицы не могут возникать в вакууме, они существуют только в кристалле. Импульс фонона обладает своеобразным свойством: при столкновении фононов в кристалле их импульс может дискретными порциями передаваться кристаллической решетке — он при этом не сохраняется. Поэтому в случае фононов говорят о квазиимпульсе.
Энергия кристаллической решетки рассматривается как энергия фононного газа, подчиняющегося статистике Бозе — Эйнштейна (см. § 235), так как фононы являются бозонами (их спин равен нулю). Фононы могут испускаться и поглощаться, но их число не сохраняется постоянным; поэтому в формуле (235.1) для фононов необходимо m положить равным нулю.
Применение статистики Бозе — Эйнштейна к фононному газу — газу из невзаимодействующих бозе-частиц — привело П. Дебая к количественному выводу, согласно которому при высоких температурах, когда T > > T D (классическая область), теплоемкость твердых тел описывается законом Дюлонга и Пти (см. § 73), а при низких температурах, когда T < < T D (квантовая область), — пропорциональна кубу термодинамической температуры: СV~Т 3. В данном случае TD — характеристическая температура Дебая, определяемая соотношением kТD= 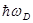 , где
, где 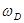 —предельная частота упругих колебаний кристаллической решетки. Таким образом, теория Дебая объяснила расхождение опытных и теоретических (вычисленных на основе классической теории) значений теплоемкости твердых тел (см. § 73 и рис. 113).
—предельная частота упругих колебаний кристаллической решетки. Таким образом, теория Дебая объяснила расхождение опытных и теоретических (вычисленных на основе классической теории) значений теплоемкости твердых тел (см. § 73 и рис. 113).
Модель квазичастиц — фононов — оказалась эффективной для объяснения открытого П. Л. Капицей явления сверхтекучести жидкого гелия (см. § 31, 75). Теория сверхтекучести, созданная (1941) Л. Д. Ландау и развитая (1947) российским ученым Н. Н. Боголюбовым (р. 1909), применена впоследствии к явлению сверхпроводимости (см. § 239).
§ 238. Выводы квантовой теории электропроводности металлов
Квантовая теория электропроводности металлов — теория электропроводности, основывающаяся на квантовой механике и квантовой статистике Ферми — Дирака, — пересмотрела вопрос об электропроводности металлов, рассмотренный в классической физике. Расчет электропроводности металлов, выполненный на основе этой теории, приводит к выражению для удельной электрической проводимости металла
 (238.1)
(238.1)
которое по внешнему виду напоминает классическую формулу (103.2) для g, но имеет совершенно другое физическое содержание. Здесь п — концентрация электронов проводимости в металле, á lF ñ — средняя длина свободного пробега электрона, имеющего энергию Ферми, á uF ñ — средняя скорость теплового движения такого электрона.
Выводы, получаемые на основе формулы (238.1), полностью соответствуют опытным данным. Квантовая теория электропроводности металлов, в частности, объясняет зависимость удельной проводимости от температуры: g ~ 1/ T (классическая теория (см. § 103) дает, что g ~1/  ), а также аномально большие величины (порядка сотен периодов решетки) средней длины свободного пробега электронов в металле (см. § 103).
), а также аномально большие величины (порядка сотен периодов решетки) средней длины свободного пробега электронов в металле (см. § 103).
Квантовая теория рассматривает движение электронов с учетом их взаимодействия с кристаллической решеткой. Согласно корпускулярно-волновому дуализму, движению электрона сопоставляют волновой процесс. Идеальная кристаллическая решетка (в ее узлах находятся неподвижные частицы и в ней отсутствуют нарушения периодичности) ведет себя подобно оптически однородной среде — она «электронные волны» не рассеивает. Это соответствует тому, что металл не оказывает электрическому току — упорядоченному движению электронов — никакого сопротивления. «Электронные волны», распространяясь в идеальной кристаллической решетке, как бы огибают узлы решетки и проходят значительные расстояния.
В реальной кристаллической решетке всегда имеются неоднородности, которыми могут быть, например, примеси, вакансии; неоднородности обусловливаются также тепловыми колебаниями. В реальной кристаллической решетке происходит рассеяние «электронных волн» на неоднородностях, что и является причиной электрического сопротивления металлов. Рассеяние «электронных волн» на неоднородностях, связанных с тепловыми колебаниями, можно рассматривать как столкновения электронов с фононами.
Согласно классической теории, á u ñ ~  , поэтому она не смогла объяснить истинную зависимость g от температуры (см. § 103). В квантовой теории средняя скорость á uF ñ от температуры практически не зависит, так как доказывается, что с изменением температуры уровень Ферми остается практически неизменным. Однако с повышением температуры рассеяние «электронных волн» на тепловых колебаниях решетки (на фононах) возрастает, что соответствует уменьшению средней длины свободного пробега электронов. В области комнатных температур á lF ñ ~Т –1, поэтому, учитывая независимость á u ñ от температуры, получим, что сопротивление металлов (R ~ 1/g) в соответствии с данными опытов растет пропорционально Т. Таким образом, квантовая теория электропроводности металлов устранила и эту трудность классической теории.
, поэтому она не смогла объяснить истинную зависимость g от температуры (см. § 103). В квантовой теории средняя скорость á uF ñ от температуры практически не зависит, так как доказывается, что с изменением температуры уровень Ферми остается практически неизменным. Однако с повышением температуры рассеяние «электронных волн» на тепловых колебаниях решетки (на фононах) возрастает, что соответствует уменьшению средней длины свободного пробега электронов. В области комнатных температур á lF ñ ~Т –1, поэтому, учитывая независимость á u ñ от температуры, получим, что сопротивление металлов (R ~ 1/g) в соответствии с данными опытов растет пропорционально Т. Таким образом, квантовая теория электропроводности металлов устранила и эту трудность классической теории.
§ 239. Сверхпроводимость. Понятие об эффекте Джозефсона
Преждечем на основе квантовой теории приступить к качественному объяснению явления сверхпроводимости, рассмотрим некоторые свойства сверхпроводников.
|
|
