
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Законы Кирхгофа для магнитных цепей.
|
|
Законы Кирхгофа для магнитных цепей. При расчетах магнитных цепей, как и электрических, используют первый и второй законы (правила) Кирхгофа.
Первый закон Кирхгофа: алгебраическая сумма магнитных потоков в любом узле магнитной цепи равна нулю:

Первый закон Кирхгофа для магнитных цепей следует из принципа непрерывности магнитного потока, известного из курса физики (см. также § 21.8 [1]).
Второй закон Кирхгофа: алгебраическая сумма падений магнитного напряжения, вдоль любого замкнутого контура равна алгебраической сумме МДС вдоль того же контура:

Второй закон Кирхгофа для магнитных цепей, по сути дела, есть иная форма записи закона полного тока.
Перед тем как записать уравнения по законам Кирхгофа, следует произвольно выбрать положительные направления потоков в ветвях и положительные направления обхода контуров.
Если направление магнитного потока на некотором участке совпадает с направлением обхода, то падение магнитного напряжения
этого участка входит в сумму ∑ Um со знаком плюс, если встречно ему, то со знаком минус.
Аналогично, если МДС совпадает с направлением обхода, она входит в ∑ Iw со знаком плюс, в противном случае — со знаком минус.

В качестве примера составим уравнения по законам Кирхгофа для разветвленной магнитной цепи, изображенной на рис. 14.12.
Левую ветвь назовем первой, и все относящиеся к ней величины запишем с индексом I (поток Ф1, напряженность поля H1, длина пути в стали l 1, длина воздушного зазора δ 1, МДС I1w1).
Среднюю ветвь назовем второй, и все относящиеся к ней величины будут соответственно с индексом 2 (поток Ф2, напряженность поля H2, длина пути в стали l2, длина воздушного зазора δ 2, МДС I2w2).
Все величины, относящиеся к правой ветви, имеют индекс 3 (поток Ф3, длина пути на вертикальном участке l ΄ 3, суммарная длина пути на двух горизонтальных участках l ΄ ΄ 3 ).
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Произвольно выберем направление потоков в ветвях. Положим, что все потоки (Ф1, Ф2, Ф3) направлены вверх (к узлу а). Число уравнений, которые следует составить по законам Кирхгофа, должно быть равно числу ветвей цепи (в рассматриваемом случае нужно составить три уравнения).
По первому закону Кирхгофа необходимо составить столько уравнений, сколько в цепи узлов без единицы (см. § 2.8 [1]).
В цепи (рис. 14.12) два узла; следовательно, по первому закону Кирхгофа составим одно уравнение:

По второму закону Кирхгофа следует составить число уравнений, равное числу ветвей, за вычетом числа уравнений, составленных по первому закону Кирхгофа. В рассматриваемом примере по второму закону Кирхгофа составим 3 — 1 = 2 уравнения.
Первое из этих уравнений составим для контура, образованного первой и второй ветвями, второе — для контура, образованного первой и третьей ветвями (для периферийного контура).
Перед составлением уравнений по второму закону Кирхгофа необходимо выбрать положительное направление обхода контуров. Будем обходить контуры по часовой стрелке.
Уравнение для контура, образованного первой и второй ветвями, имеет вид

где Hδ 1 и Hδ 2 — напряженности поля соответственно в воздушных зазорах δ 1 и δ 2.
В левую часть уравнения вошли слагаемые H1l1 и Hδ 1δ 1 со знаком плюс, так как на первом участке поток Ф1 направлен согласно с обходом контура, слагаемые H1l1 и Hδ 2δ 2 — со знаком минус, так как поток Ф2 направлен встречно обходу контура.
В правую часть уравнения МДС I1w1 вошла со знаком плюс, так как она направлена согласно с обходом контура, а МДС I2w2 — со знаком минус, так как она направлена встречно обходу контура.
Составим уравнение для периферийного контура, образованного первой и третьей ветвями:

Совместно решать уравнения (а) — (в) с тремя неизвестными (Ф1, Ф2, Ф3) не будем, так как в § 14.8 [1] дается решение рассматриваемой задачи более совершенным методом, чем метод на основе законов Кирхгофа — методом двух узлов.
Применение к магнитным цепям всех методов, используемых для расчета электрических цепей с нелинейными резисторами. В гл. 13 [1] подробно рассматривались различные методы расчета электрических цепей с НР. Эти методы полностью применимы и к расчету магнитных цепей, так как и магнитные и электрические цепи подчиняются одним и тем же законам — законам Кирхгофа.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Аналогом тока в электрической цепи является поток в магнитной цепи, аналогом ЭДС — МДС, аналогом вольт-амперной характеристики нелинейного резистора — вебер-амперная характеристика участка магнитной цепи.
Электромагнитные устройства
Катушка с магнитопроводом в цепи переменного тока


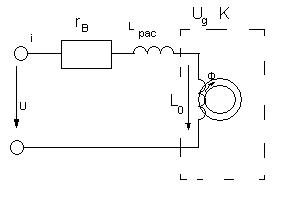

Ψ =  + wФ=
+ wФ= 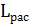 ί + wФ
ί + wФ
U=  ί +
ί +  +
+ 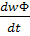 =
=  ί +
ί + 
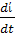 + w
+ w  =
=  ί +
ί + 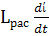 + w
+ w  =
=  ί +
ί +  +
+  = =
= =  +
+  +
+ 
Идеализированная катушка

 = -
= -  ;
;  =
=  sinω t
sinω t
 =
=  sinω t = W
sinω t = W  =>
=>  =
=  sinω t
sinω t  =>
=>
Ф = 
 = -
= -  cos
cos  + A
+ A
A=0 – в установившемся режиме
Ф= -  cos
cos  =
=  sin(ω t -
sin(ω t -  ) =
) =  sin(ω t -
sin(ω t - 
= > 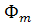 =
=  =
=  ,
,  = 4.44
= 4.44  - трансформаторная ЭДС
- трансформаторная ЭДС
Уравнения, схемы замещения и векторная диаграммыреальной катушки
1) Линейный характер  = B=
= B=  H
H
Ф = BS =  HS; H
HS; H  = ί w => H =
= ί w => H = 
Ф =  т.к. U =
т.к. U =  ί +
ί + 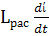 + L
+ L 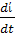 =>
=>
U =  +
+ 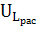 +
+ 

2) Округлая статическая петля гистерезиса
B=  sin
sin  , H=
, H=  sin
sin 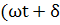 ) =>
) => 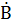 =
=  ,
,  =
=  = >
= >  =
= 
 =
= 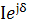
 =-
=-  =
= 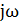 w
w 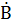 S=
S= 
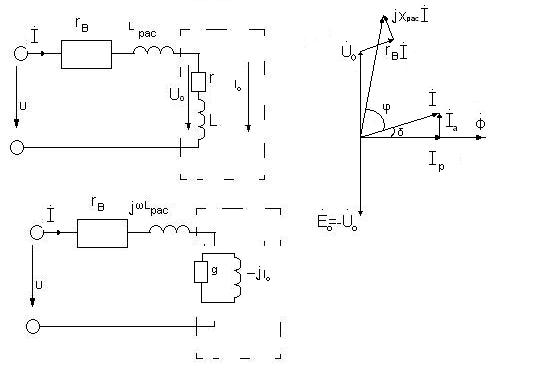
Z=  =
=  =
= 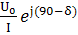 =
=  sin
sin  +
+  cos
cos  =
= 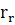 +
+  =
= 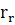 +
+ 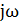 L
L
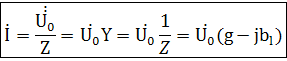
Трансформаторы.
|
|
