Приклад 4.

;

1. Знаходимо відносну похибку по пунктах:

а)

б)

в)

г)

2. Розраховуємо по розрахунковій формулі (1) середній

результат .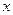

3. За формулою (3) знаходимо абсолютну похибку

вимірювання

.

4. Кінцеве значення дійсної величини буде:

.

Метод логарифмування з подальшим диференціюванням зручно використовувати, якщо розрахункова формула має вигляд добутків, часток та степенів.

Потрібно пам’ятати, що точність результату визначається точністю вимірювальних приладів і акуратністю вихідних вимірювань і не може бути збільшена в подальшому шляхом штучного набирання знаків при виконанні арифметичних дій.

Абсолютну похибку непрямого вимірювання заокруглюють до однієї значущої цифри.

Відносну похибку непрямого вимірювання заокруглюють до двох значущих цифр.

В наближеному числі усі цифри повинні бути вірними, за винятком останньої цифри.

В подальшому будемо користуватись таким поняттям, як ”десяткові знаки” та ”значущі цифри”.

Кількість десяткових знаків числа визначаються кількістю цифр, які стоять після коми, разом з нулями.

.

Значущими цифрами називають усі правильні цифри (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) окрім нулів на початку числа.

Наприклад:

Якщо знаходити значення похибок непотрібно, то при арифметичних діях з наближеними числами користуються наступними правилами заокруглення.

1. При додаванні та відніманні результат повинен зберігати стільки десяткових знаків, скільки їх має число з найменшою кількістю десяткових знаків та усі доданки можна заокруглювати:

2. При множенні та діленні результат повинен зберігати стільки значущих цифр, скільки їх має число з найменшою кількістю значущих цифр:

3. При піднесенні до степеня результат зберігає стільки значущих цифр, скільки їх має основа:

;

4. При знаходженні логарифму в результаті залишається стільки значущих цифр, скільки їх у числі, від якого брали логарифм:

5. Правила оформлення результатів лабораторної роботи.

Після виконання лабораторної роботи з фізики оформляється звіт на подвійному листку зі звичайного зошита, або на аркушах формату А4.

На титульній сторінці вказують:

Українська академія друкарства

кафедра математики і фізики

Звіт

про виконання лабораторної роботи №___

на тему: _________________________

студента групи ___________________

Прізвище І.Б.

На першій сторінці записують:

1. Теорія (теоретичні відомості)

В цьому пункті описують основні фізичні закони та параметри, які використовують та досліджують в даній роботі.

На другій сторінці записують:

2. Рисунок (схема установки) та робоча формула.

Опис цього пункту займає, приблизно, 0, 5 сторінки.

Прямі вимірювання	Непряме вимірювання з його похибками
M	P	R	T	ρ	∆ ρ	Eρ
кг/моль	Па	Дж/моль·К	К	кг/м 3	кг/м 3	%

3. Таблиця результатів вимірювань.

На третій сторінці записують:

4. Методика знаходження похибок

а) прямих вимірювань

, яким методом;

, яким методом;

, яким методом;

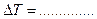, яким методом.

б) непрямого вимірювання

.

ЧАСТИНА 2. МЕХАНІКА

Лабораторна робота № 1.01 Визначення прискорення вільного падіння за допомогою фізичного маятника

Вступ

Фізичним маятником називається тверде тіло, яке під дією сили тяжіння здійснює коливний рух навколо горизонтальної осі, що не проходить через його центр інерції. При малих кутах відхилення маятник здійснює гармонічні коливання, які описуються диференціальним рівнянням:

, (1)

де – кут відхилення маятника від вертикального положення, – момент інерції маятника відносно осі коливань, – маса маятника. Це рівняння одержане на основі другого закону Ньютона для обертового руху. Розв'язком рівняння є функція виду:

, (2)

де – циклічна частота власних коливань маятника. Так як , то період коливання маятника

. (3)

У формулі (3) вираз має розмірність довжини і називається приведеною довжиною фізичного маятника. Період коливання фізичного маятника з приведеною довжиною і математичного маятника такої ж довжини співпадають:

. (4)

Метод визначення прискорення вільного падіння

Згідно з формулою (4) прискорення вільного падіння можна визначити по періоду 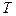коливань маятника, якщо відома його приведена довжина .

При паралельному переносі осі коливання маятника вздовж прямої, що з’єднує цю вісь і центр тяжіння маятника, на віддаль приведеної довжини маятник буде коливатися з однаковим періодом.

Рис. 1.1

У цій роботі використовується маятник (рис. 1.1), що представляє собою стержень з двома нерухомо закріпленими паралельними одна одній тригранними опорними призмами 2, на яких він може почергово підвішуватися на кронштейні 3, та сочевицями 4 і 5. Такої конструкції маятник називається оборотним. Сочевиця 4 закріплена нерухомо, а друга – 5 може переміщатися вздовж стержня. Положення сочевиці 5 на стержні визначається по шкалі 6.

ля полегшення підрахунку числа коливань маятника в роботі використовується автоматичний лічильник, що працює синхронно з електросекундоміром.