Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Завдання. 1. Встановити всі чотири вантажі на віддалі , від осі стержня

1. Встановити всі чотири вантажі на віддалі , від осі стержня. Привести маятник в коливний рух, для чого повернути хрестовину довкола вертикальної осі на невеликий кут (не більше 10°) і залишити їй свободу руху. За допомогою секундоміру виміряти час двадцяти коливань і вирахувати період коливань . Вимірювання провести не менше 5-ти разів і знайти середнє значення періоду .

2. Аналогічно провести вимірювання для положення всіх чотирьох вантажів на віддалі від осі стержня і знайти середнє значення періоду .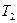

3. Виміряти довжину стержня і, за допомогою мікрометра, діаметр стержня. Вимірювання цих розмірів провести декілька разів і визначити середнє значення і 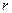. Зважуванням знайти масу вантажу .

4. Підставивши у формулу (9) середнє значення виміряних величин, вирахувати модуль зсуву. Оцінити похибки визначення модуля зсуву.

Вказівки до виконання завдання

1. Після того, як маятник приведений у коливний рух, необхідно слідкувати, щоб він не здійснював коливань довкола горизонтальної осі і його коливання проходили тільки довкола вертикальної осі стержня.

2. Вимірювання періоду коливання необхідно починати після встановлення стабільної амплітуди (приблизно через 30-40 секунд після початку коливань).

3. Відлік часу коливань слід починати в той момент, коли хрестовина знаходиться в положенні максимального відхилення від положення рівноваги.

4. При вимірюванні періоду коливань потрібно слідкувати, щоб кут повороту маятника довкола осі не перевищував 10°.

5. Віддалі і потрібно вимірювати від центра вантажу до осі стержня.

Контрольні запитання:

1. Що таке межа пружності?

2. Який фізичний зміст модуля зсуву?

3. Яка методика визначення моменту інерції маятника в даній роботі?

Лабораторна робота № 1.05. Визначення моментів інерції тіл методом крутильних коливань

Вступ

Момент інерції (динамічний момент інерції) є мірою інертності системи, що обертається.

Для окремої матеріальної точки, що здійснює обертовий рух, момент інерції відносно заданої осі дорівнює добутку маси цієї точки на квадрат віддалі до осі обертання:

. (1)

Момент інерції відносно осі дорівнює сумі моментів інерції складових його частин (матеріальних точок) відносно цієї осі:

, (2)

де і 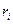– маса матеріальної точки і її віддаль до осі обертання, – число матеріальних точок, на яке можна розбити тіло.

Як видно з (2), момент інерції тіла є величина адитивна, тобто момент інерції тіла дорівнює сумі моментів інерції його частин і момент інерції системи тіл дорівнює сумі моментів інерції окремих тіл. Одне і те ж тіло має різні моменти інерції відносно різних осей. Важливою динамічною характеристикою тіла є його момент інерції відносно осі, що проходить через центр інерції (центр мас) тіла, оскільки момент інерції тіла відносно довільної іншої осі можна представити, згідно з теоремою Штейнера, як суму моментів інерції тіла відносно осі, що проходить через центр інерції тіла паралельно даній, і добутку маси тіла на квадрат віддалі між осями:

. (3)

Момент інерції тіла залежить від його маси, конфігурації і розподілу мас в тілі відносно осі обертання. Для однорідних тіл правильної геометричної форми моменти інерції можна знайти шляхом розрахунку. Так моменти інерції циліндра (диску) і кулі відносно їх геометричних осей дорівнює

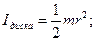
(4)

де і 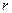– маса і радіус вказаних тіл. Є різні методи експериментального визначення моментів інерції любих тіл. В цій роботі моменти інерції визначаються методом крутильних коливань трифілярного підвісу.

Метод вимірювань

Рис. 1.8

Трифілярний підвіс представляє собою круглу платформу, підвішену на трьох симетрично розташованих пружних нитках, які симетрично прикріплені до кільця меншого діаметра (рис. 1.8). Якщо платформу повернути на деякий кут відносно вертикальної осі, що проходить через її середину, і залишити їй свободу руху, то вона буде здійснювати крутильні коливання довкола цієї осі, причому центр інерції платформи в процесі її коливань буде переміщатися вверх і вниз по осі обертання. Суть цього методу полягає у вимірюванні періоду коливань, який визначається моментом інерції трифілярного підвісу відносно осі коливань. Співвідношення між моментом інерції трифілярного підвісу і періодом його крутильних коливань можна знайти на основі закону збереження енергії. При малих кутах повороту платформа здійснює гармонічні крутильні коливання, що описуються рівнянням:

, (5)

де – кут повороту (кутове зміщення) платформи в момент часу , – кутова амплітуда, – період коливань. Кутова швидкість обертання:

, (6)

Як видно із формули (6) абсолютне максимальне значення кутової швидкості , яку має платформа, переходячи через положення рівноваги, дорівнює

. (7)

Цьому значенню кутової швидкості платформи відповідає її кінетична енергія , рівна

, (8)

де – момент інерції платформи. У результаті повороту платформи довкола вертикальної осі на максимальний кут її центр інерції переміститься по цій осі. Відносно положення рівноваги на висоту 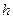, що відповідає приросту потенціальної енергії платформи на величину

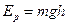, (9)

Висоту підйому платформи легко виразити через параметри трифілярного підвісу: довжини ниток підвісу , радіус платформи і радіус кільця . Відповідний розрахунок, враховуючи, що кут малий, дає

. (10)

За законом збереження енергії:

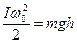. (11)

Підставивши останній вираз у рівняння (10) знайдемо:

(12)

По формулі (12) можна, вимірявши період коливань, визначити момент інерції як самої платформи, так і тіла, яке навантажене на платформу, оскільки, як про це сказано вище, момент інерції системи тіл дорівнює сумі моментів інерції тіл, що складають систему.