Случай произвольной области

Теорема 7. Пусть выполнены следующие условия: 1) область D ограничена, замкнута и такова, что любая прямая, параллельная оси Oy, пересекает границу этой области не более чем в двух точках, ординаты которых суть y ₁(x) и y ₂(x), где y ₁(x) ≤ y ₂(x) (см. Рис. 1); 2) функция f (x, y) допускает существование двойного интеграла

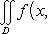
и существование для любого x однократного интеграла

При этих условиях существует повторный интеграл

(x ₁ и x ₂ - наименьшая и наибольшая абсциссы точек области D) и справедливо равенство

(19)

Доказательство. Обозначим через R прямоугольник со сторонами, параллельными координатным осям, содержащий область D, а через F (x, y) - функцию, совпадающую с f (x, y) в точках области D и равную нулю в остальных точках R. Для функции F (x, y) в прямоугольнике R выполнены все условия теоремы 7, и, стало быть, справедлива формула (13), которая (с учетом того, что F (x, y) равна нулю вне D и совпадает с f (x, y) в D) переходит в формулу (19). Теорема доказана.

Замечание 1. В теореме 7 можно поменять ролями x и y, т. е. можно предположить, что выполнены следующие два условия: 1) область D такова, что любая прямая, параллельная оси Ox, пересекает границу этой области не более чем в двух точках, абсциссы которых x ₁(y) и x ₂(y), где x ₁(y) ≤ x ₂(y) (см. Рис. 2); 2) функция f (x, y) допускает существование по области D двойного интеграла и существование для любого y однократного интеграла

При выполнении этих двух условий существует повторный интеграл

(y ₁ и y ₂ - наименьшая и наибольшая ординаты точек области D) и справедливо равенство

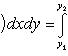
(19')

Пример. Пусть область D - круг x ² + y ² ≤ R ² (см. Рис. 3), а f (x, y) = x ²(R ² - y ²)^3/2. Любая прямая, параллельная оси Ox, пересекает границу D не более чем в двух точках, абсциссы которых и (см. Рис. 3). Поэтому применяя формулу (19'), получим

Замечание 2. В случае, если область D не удоволетворяет требованиям теоремы 7 или замечания 1 к этой теореме, часто удается разбить эту область на сумму конечного числа областей такого типа, не имеющих общих внутренних точек. Тогда интеграл по области D, в силу свойства аддитивности, равен сумме интегралов по соответствующим областям. Так, область D, изображенную на Рис. 4, удается разбить на сумму трех областей D ₁, D ₂ и D ₃, к каждой из которых применима теорема 7 или замечание 1.