Сортування злиттям.

В основі цього способу сортування лежить злиття двох упорядкованих ділянок масиву в одну впорядковану ділянку іншого масиву. Злиття двох упорядкованих послідовностей можна порівняти з перебудовою двох колон солдатів, вишикуваних за зростом, в одну, де вони також розташовуються за зростом. Якщо цим процесом керує офіцер, то він порівнює зріст солдатів, перших у своїх колонах і вказує, якому з них треба ставати останнім у нову колону, а кому залишатися першим у своїй. Так він вчиняє, поки одна з колон не вичерпається— тоді решта іншої колони додається до нової.

Під час сортування в дві допоміжні черги з основної поміщаються перші дві відсортовані підпослідовності, які потім зливаються в одну і результат записується в тимчасову чергу. Потім з основної черги беруться наступні дві відсортовані підпослідовності і так до тих пір доки основна черга не стане порожньою. Після цього послідовність з тимчасової черги переміщається в основну чергу. І знову продовжується сортування злиттям двох відсортованих підпослідовностей. Сортування триватиме до тих пір поки довжина відсортованої підпослідовності не стане рівною довжині самої послідовності.

Схема алгоритму для конкретного прикладу послідовності

Проілюструємо алгоритм сортування на такій послідовності: 42 5 30 36 25 10 37 49 0 0 На початку сортування відсортовані підпослідовності містять в собі по одному елементу.

Крок 1: 5 42 | 30 36 | 10 25 | 37 49 | 0 0

Крок 2: 5 30 36 42 | 10 25 37 49 | 0 0

Крок 3: 5 10 25 30 36 37 42 49 | 0 0

Крок 4: 0 0 5 10 25 30 36 37 42 49

Самою найважливішою частиною алгоритму є злиття двох впорядкованих множин. Цю частину алгоритму опишемо більш детально.

1. Початкові установки. Визначити довжини першої і другої початкових множин – l1 і l2 відповідно. Встановити індекси поточних елементів в початковій множині і1 і і2 в 0. Встановити індекс в вихідній множині j=1.

2. Цикл злиття. Виконувати крок 3 до тих пір, поки і1< =l1 і і2< =l2.

3. Порівняння. Порівняти ключ і1 -го елемента з першої початкової множини з ключем і2 -го елемента з другої початкової множини. Якщо ключ елемента з 1-ої множини менший, то записати і1 -тий елемент з 1-ої множини на j -те місце в вихідній множині і збільшити і1 на 1. Інакше – записати і2 -тий елемент з 2-ої множини на j -те місце в вихідній множині і збільшити і2 на 1. Збільшити j на 1.

4. Виведення залишків. Якщо і1< =l1, то переписати частину 1-ої початкової множини від і1 до l1 включно в вихідну множину. Інакше – переписати частину 2-ої початкової множини від і2 до l2 включно в вихідну множину.

Принципи рандомізації.

В деяких програмах потрібно виконання операцій, протилежних сортуванню. Отримавши множину елементів, програма повинна розмістити їх у випадковому порядку. Рандомізацію нескладно виконати, використовуючи алгоритм, подібний на сортування вибіркою.

Для кожного розміщення в множині, алгоритм випадковим чином вибирає елемент, який повинен його зайняти з тих, які ще не були розміщені на своєму місці. Потім цей елемент міняється місцями з елементом, який, знаходиться на цій позиції. Так як алгоритм заповнює кожну позицію лише один раз, його складність – O(N).

Нескладно показати, що імовірність того, що елемент виявиться на якій-небудь позиції, рівна 1/N. Оскільки елемент може виявитися на будь-якій позиції з однаковою імовірністю, цей алгоритм дійсно приводить до випадкового розміщення елементів.

Результат рандомізації залежить від того, наскільки ефективним є генератор випадкових чисел. Для даного алгоритми не важливий початковий порядок розміщення елементів. Якщо необхідно неодноразово рандомізувати множину елементів, немає необхідності її попередньо сортувати.

Постановка задачі пошуку.

Одна з тих дій, які найбільш часто зустрічаються в програмуванні – пошук. Існує декілька основних варіантів пошуку, і для них створено багато різноманітних алгоритмів.

Задача пошуку – відшукати елемент, ключ якого рівний заданому „аргументу пошуку”. Отриманий в результаті цього індекс забезпечує доступ до усіх полів виявленого елемента.

43.Послідовний пошук.
Найпростішим методом пошуку елемента, який знаходиться в неврегульованому наборі даних, за значенням його ключа є послідовний перегляд кожного елемента набору, який продовжується до тих пір, поки не буде знайдений потрібний елемент. Якщо переглянуто весь набір, і елемент не знайдений – значить, шуканий ключ відсутній в наборі. Цей метод ще називають методом повного перебору.

Для послідовного пошуку в середньому потрібно N/2 порівнянь. Таким чином, порядок алгоритму – лінійний – O(N).

Програмна ілюстрація лінійного пошуку в неврегульованому масиві приведена в наступному прикладі, де a – початковий масив, key – ключ, який шукається; функція повертає індекс знайденого елемента.

int LinSearch(int *a, int key)

{

int i = 0;

while ((i< N) & & (a[i]! = key))

i++;

return i;

}

Якщо елемент знайдено, то він знайдений разом з мінімально можливим індексом, тобто це перший з таких елементів. Рівність i=N засвідчує, що елемент відсутній.

Єдина модифікація цього алгоритму, яку можна зробити, – позбавитися перевірки номера елементу масиву в заголовку циклу (i< N) за рахунок збільшення масиву на один елемент у кінці, значення якого перед пошуком встановлюють рівним шуканому ключу – key – так званий „бар’єр”.

int LinSearch(int *a, int key)

{

a[N] = key;

i = 0;

while (a[i]! = key)

i++;

return i; // i< N – повернення номера елемента

}

44.Бінарний пошук.
Іншим, відносно простим, методом доступу до елемента є метод бінарного (дихотомічного) пошуку, який виконується в явно впорядкованій послідовності елементів. Записи в таблицю заносяться в лексикографічному (символьні ключі) або чисельно (числові ключі) зростаючому порядку. Для досягнення впорядкованості може бути використаний котрийсь з методів сортування, які розглянемо пізніше.

Оскільки шуканий елемент швидше за все знаходиться „десь в середині”, перевіримо саме середній елемент: a[N / 2] == key? Якщо це так, то знайдено те, що потрібно. Якщо a[N / 2] < key, то значення i = N / 2 є замалим і шуканий елемент знаходиться „праворуч”, а якщо a[N / 2] > key, то „ліворуч”, тобто на позиціях 0 … i.

Для того, щоб знайти потрібний запис в таблиці, у гіршому випадку потрібно log2(N) порівнянь. Це значно краще, ніж при послідовному пошуку.

Приведемо ілюстрація бінарного пошуку на прикладі.

int BinSearch(int *a, int key)

{

int b, e, i;

b = 0; e = N-1; // початкові значення меж

bool Found = false; // прапорець

while ((b < e) & &! Found) // цикл, поки інтервал пошуку не звузиться до 0

{

i = (b + e) / 2; // середина інтервалу

if (a[i] == key)

Found = true; // ключ знайдений

else

if (a[i] < key)

b = i + 1; // пошук в правому підінтервалі

else

e = i - 1; // пошук в лівому підінтервалі

}

return i;

}

Максимальна кількість порівнянь для цього алгоритму рівна log2(N). Таким чином, приведений алгоритм суттєво виграє у порівнянні з лінійним пошуком.

Ефективність дещо покращиться, якщо поміняти місцями заголовки умовних операторів. Перевірку на рівність можна виконувати в другу чергу, так як вона зустрічається лише одноразово і приводить до завершення роботи. Але більш суттєвий виграш дасть відмова від завершення пошуку при фіксації знаходження елемента.

int BinSearch(int *a, int key)

{

int b, e, i;

b = 0; e = N-1;

while (b< e)

{

i = (b + e) / 2;

if (а[m] < x)

b = i + 1;

else

e = i - 1;

}

return i

}

Завершення циклу гарантовано. Це пояснюється наступним. На початку кожного кроку b< e. Для середнього арифметичного i справедлива умова b< =i< e. Значить, різниця e-b дійсно спадає, тому що або b збільшується при присвоєнні йому значення i+1, або e зменшується при присвоєнні йому значення i-1. При b< =i повторення циклу закінчується.

Виконання умови b=e ще не засвідчує знаходження потрібного елемента. Тут потрібна додаткова перевірка. Також, необхідно враховувати, що елемент a[e] у порівняннях ніколи не бере участі. Значить, і тут необхідна додаткова перевірка на рівність a[e]=key. Але ці перевірки виконуються однократно.

Алгоритм бінарного пошуку можна представити і трохи інакше, використовуючи рекурсивний опис. В цьому випадку граничні індекси інтервалу b і e є параметрами алгоритму. Рекурсивна процедура бінарного пошуку представлена в наступній програмі. Для виконання пошуку необхідно при виклику процедури задати значення її формальних параметрів b і е – 0 і N-1 відповідно, де b, e – граничні індекси області пошуку.

int BinSearch(int *a, int key, int & b, int & e)

{

int i;

if (b > e)

return -1; // перевірка ширини інтервалу

else

{

i = (b + e) / 2; // середина інтервалу

if (a[i] == key)

return i; // ключ знайдений, повернення індексу

else

if (a[i] < key) // пошук в правому підінтервалі

return BinSearch(a, key, i+1, e);

else // пошук в лівому підінтервалі

return BinSearch(a, key, b, i-1);

}

}

Відомо, також, декілька модифікацій алгоритму бінарного пошуку, які виконуються на деревах.

45.Пошук методом інтерполяції.
Якщо немає ніякої додаткової інформації про значення ключів, крім факту їхнього впорядкування, то можна припустити, що значення key збільшуються від a[0] до a[N-1] більш-менш „рівномірно”. Це означає, що значення середнього елементу a[N / 2] буде близьким до середнього арифметичного між найбільшим та найменшим значенням. Але, якщо шукане значення key відрізняється від вказаного, то є деякий сенс для перевірки брати не середній елемент, а „середньо-пропорційний”, тобто такий, номер якого пропорційний значенню key:

Програмна реалізація такого варіанту пошуку матиме вигляд:

int BinSearch(int *a, int key)

{

int b, e, i;

b = 0; e = N-1; // початкові значення меж

while (b < e) // цикл, поки інтервал пошуку не звузиться до 0

{

i = b + (key – a[b])*(e-b) / (a[e] – a[b]);

if (a[i] == key)

return i; // ключ знайдений - повернення індексу

else

if (a[i] < key)

b = i + 1; // пошук в правому підінтервалі

else

e = i - 1; // пошук в лівому підінтервалі

}

return -1; // ключ не знайдений

}

Вираз для поточного значення i одержано з пропорційності відрізків на рисунку:

В середньому цей алгоритм має працювати швидше за бінарний пошук, але у найгіршому випадку буде працювати набагато довше.

46.Пошук методом „золотого перерізу”.
Деякий ефект дає використання так званого „золотого перерізу”. Це число , що має властивість:

Доданій корінь і є золотим перерізом.

Згідно цього алгоритму відрізок b … e слід ділити не навпіл, як у бінарному алгоритмі, а на відрізки, пропорційні та 1, в залежності від того, до якого краю ближче key. Замість оператора

i = …;

у програму бінарного пошуку слід внести наступний фрагмент, попередньо визначивши константу Phi:

if a[e] - key < key - a[b]

i = b + (e - b) * (Phi - 1);

else

i = e - (e - b) * (Phi - 1) + 1;

47.Алгоритми пошуку послідовностей.
Даний клас задача відноситься до задачі пошуку слів у тексті. Нехай масив a[N] вважається масивом символів останній елемент якого – 0:

char a[N];

у якому слід знайти заданий рядок символів: 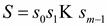довжиною m.

48.Хешування даних.
Для прискорення доступу до даних можна використовувати попереднє їх впорядкування у відповідності зі значеннями ключів. При цьому можуть використовуватися методи пошуку в упорядкованих структурах даних, наприклад, метод дихотомічного пошуку, що суттєво скорочує час пошуку даних за значенням ключа. Проте при добавленні нового запису потрібно дані знову впорядкувати. Втрати часу на повторне впорядкування можуть значно перевищувати виграш від скорочення часу пошуку. Тому для скорочення часу доступу до даних використовується так зване випадкове впорядкування або хешування. При цьому дані організуються у вигляді таблиці за допомогою хеш-функції h, яка використовується для „обчислення” адреси за значенням ключа.

У попередній главі описувався алгоритм інтерполяційного пошуку, який використовує інтерполяцію для пришвидшення пошуку. Порівнюючи шукане значення зі значеннями елементів у відомих точках, цей алгоритм може визначити імовірне розміщення шуканого елемента. По суті, він створює функцію, яка встановлює відповідність між шуканим значенням і індексом позиції, в якій він повинен знаходитися. Якщо перше передбачення помилкове, то алгоритм знову використовує цю функцію, передбачаючи нове розміщення, і так далі, до тих пір, поки шуканий елемент не буде знайдено.

Хешування використовує аналогічний підхід, відображаючи елементи в хеш-таблиці. Алгоритм хешування використовує деяку функцію, яка визначає імовірне розміщення елемента в таблиці на основі значення шуканого елементу.

Ідеальною хеш-функцією є така хеш-функція, яка для будь-яких двох неоднакових ключів дає неоднакові адреси. Підібрати таку функцію можна у випадку, якщо всі можливі значення ключів відомі наперед. Така організація даних носить назву „досконале хешування”.

Наприклад, потрібно запам’ятати декілька записів, кожен з яких має унікальний ключ зі значенням від 1 до 100. Для цього можна створити масив з 100 комірками і присвоїти кожній комірці нульовий ключ. Щоб добавити в масив новий запис, дані з нього просто копіюються у відповідну комірку масиву. Щоб добавити запис з ключем 37, дані з нього копіюються в 37 позицію в масиві. Щоб знайти запис з певним ключем – вибирається відповідна комірка масиву. Для вилучення запису ключу відповідної комірки масиву просто присвоюється нульове значення. Використовуючи цю схему, можна добавити, знайти і вилучити елемент із масиву за один крок.

У випадку наперед невизначеної множини значень ключів і обмеженні розміру таблиці підбір досконалої функції складний. Тому часто використовують хеш-функції, які не гарантують виконанні умови.

Наприклад, база даних співробітників може використовувати в якості ключа ідентифікаційний номер. Теоретично можна було б створити масив, кожна комірка якого відповідала б одному з можливих чисел; але на практиці для цього не вистарчить пам’яті або дискового простору. Якщо для зберігання одного запису потрібно 1 КБ пам’яті, то такий масив зайняв би 1 ТБ (мільйон МБ) пам’яті. Навіть якщо можна було б виділити такий об’єм пам’яті, така схема була б дуже неекономною. Якщо штат фірми менше 10 мільйонів співробітників, то більше 99 процентів масиву буде пустою.

Щоб вирішити цю проблему, схеми хешування відображають потенційно велику кількість можливих ключів на достатньо компактну хеш-таблицю. Якщо на фірмі працює 700 співробітників, можна створити хеш-таблицю з 1000 комірок. Схема хешування встановлює відповідність між 700 записами про співробітників і 1000 позиціями в таблиці. Наприклад, можна розміщати записи в таблиці у відповідності з трьома першими цифрами ідентифікаційного номеру. При цьому запис про співробітника з номером 123456789 буде знаходитися в 123 комірці таблиці.

Очевидно, що оскільки існує більше можливих значень ключа, ніж комірок в таблиці, то деякі значення ключів можуть відповідати одним і тим коміркам таблиці. Даний випадок носить назву „колізія”, а такі ключі називаються „ключі-синоніми”.

Щоб уникнути цієї потенційної проблеми, схема хешування повинна включати в себе алгоритм вирішення конфліктів, який визначає послідовність дій у випадку, якщо ключ відповідає позиції в таблиці, яка вже зайнята іншим записом.

Усі методи використовують для вирішення конфліктів приблизно однаковий підхід. Вони спочатку встановлюють відповідність між ключем запису і розміщенням в хеш-таблиці. Якщо ця комірка вже зайнята, вони відображають ключ на іншу комірку таблиці. Якщо вона також вже зайнята, то процес повторюється знову до тих пір, поки нарешті алгоритм не знайде пусту комірку в таблиці. Послідовність позицій, які перевіряються при пошуку або вставці елемента в хеш-таблицю, називається тестовою послідовністю.

В результаті, для реалізації хешування необхідні три речі:

• Структура даних (хеш-таблиця) для зберігання даних;

• Функція хешування, яка встановлює відповідність між значеннями ключа і розміщенням в таблиці;

• Алгоритм вирішення конфліктів, який визначає послідовність дій, якщо декілька ключів відповідають одній комірці таблиці.

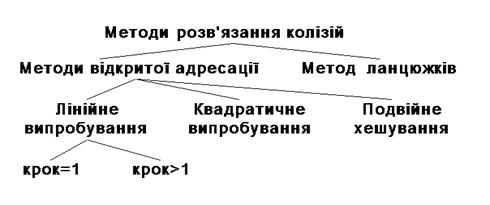
49.Алгоритми розв’язання колізій при хешуванні.
Для розв’язання колізій використовуються різноманітні методи, які в основному зводяться до методів „ланцюжків” і „відкритої адресації”.

Методом ланцюжків називається метод, в якому для розв’язання колізій у всі записи вводяться покажчики, які використовуються для організації списків – „ланцюжків переповнення”. У випадку виникнення колізій при заповненні таблиці в список для потрібної адреси хеш-таблиці добавляється ще один елемент.

Пошук в хеш-таблиці з ланцюжками переповнення здійснюється наступним чином. Спочатку обчислюється адреса за значенням ключа. Потім здійснюється послідовний пошук в списку, який зв’язаний з обчисленим адресом.

Процедура вилучення з таблиці зводиться до пошуку елемента в його вилучення з ланцюжка переповнення.

Схематичне зображення хеш-таблиці при такому методі розв’язання колізій приведене на наступному рисунку.

Якщо сегменти приблизно однакові за розміром, то у цьому випадку списки усіх сегментів повинні бути найбільш короткими при даній кількості сегментів. Якщо вихідна множина складається з N елементів, тоді середня довжина списків буде рівна N/B елементів. Якщо можна оцінити N і вибрати B якомога ближчим до цієї величини, то в списку буде один-два елементи. Тоді час доступу до елемента множини буде малою постійною величиною, яка залежить від N.

Одна з переваг цього методу хешування полягає в тому, що при його використанні хеш-таблиці ніколи не переповнюються. При цьому вставка і пошук елементів завжди виконується дуже просто, навіть якщо елементів в таблиці дуже багато. Із хеш-таблиці, яка використовує зв’язування, також просто вилучати елементи, при цьому елемент просто вилучається з відповідного зв’язного списку.

Один із недоліків зв’язування полягає в тому, що якщо кількість зв’язних списків недостатньо велика, то розмір списків може стати великим, при цьому для вставки чи пошуку елемента необхідно буде перевірити велику кількість елементів списку.

Метод відкритої адресації полягає в тому, щоб, користуючись якимось алгоритмом, який забезпечує перебір елементів таблиці, переглядати їх в пошуках вільного місця для нового запису.

Лінійне випробування зводиться до послідовного перебору елементів таблиці з деяким фіксованим кроком

a=h(key) + c*i,

де i – номер спроби розв’язати колізію. При кроці рівному одиниці відбувається послідовний перебір усіх елементів після поточного.

Квадратичне випробування відрізняється від лінійного тим, що крок перебору елементів нелінійно залежить від номеру спроби знайти вільний елемент

a = h(key2) + c*i + d*i²

Завдяки нелінійності такої адресації зменшується кількість спроб при великій кількості ключів-синонімів. Проте навіть відносно невелика кількість спроб може швидко привести до виходу за адресний простір невеликої таблиці внаслідок квадратичної залежності адреси від номеру спроби.

Ще один різновид методу відкритої адресації, яка називається подвійним хешуванням, базується на нелінійній адресації, яка досягається за рахунок сумування значень основної і додаткової хеш-функцій.

a=h1(key) + i*h2(key).

Розглянемо алгоритми вставки і пошуку для методу лінійного випробування.

Вставка:

1. i = 0

2. a = h(key) + i*c

3. Якщо t(a) = вільно, то t(a) = key, записати елемент і зупинитися

4. i = i + 1, перейти до кроку 2

Пошук:

1. i = 0

2. a = h(key) + i*c

3. Якщо t(a) = key, то зупинитися – елемент знайдено

4. Якщо t(a) = вільно, то зупинитися – елемент не знайдено

5. i = i + 1, перейти до кроку 2

Аналогічно можна було б сформулювати алгоритми добавлення і пошуку елементів для будь-якої схеми відкритої адресації. Відмінності будуть лише у виразі, який використовується для обчислення адреси (крок 2).

З процедурою вилучення справа складається не так просто, так як вона в даному випадку не буде оберненою до процедури вставки. Справа в тому, що елементи таблиці знаходяться в двох станах: вільно і зайнято. Якщо вилучити елемент, перевівши його в стан вільно, то після такого вилучення алгоритм пошуку буде працювати некоректно. Нехай ключ елемента, який вилучається, має в таблиці ключі синоніми. У цьому випадку, якщо за ним в результаті розв’язання колізій були розміщені елементи з іншими ключами, то пошук цих елементів після вилучення завжди буде давати негативний результат, так як алгоритм пошуку зупиняється на першому елементі, який знаходиться в стані вільно.

Скоректувати цю ситуацію можна різними способами. Самий простий із них полягає в тому, щоб проводити пошук елемента не до першого вільного місця, а до кінця таблиці. Проте така модифікація алгоритму зведе нанівець весь виграш в прискоренні доступу до даних, який досягається в результаті хешування.

Інший спосіб зводиться до того, щоб відслідкувати адреси всіх ключів-синонімів для ключа елемента, що вилучається, і при необхідності розмістити відповідні записи в таблиці. Швидкість пошуку після такої операції не зменшиться, але затрати часу на саме розміщення елементів можуть виявитися значними.

Існує підхід, який не має перерахованих недоліків. Його суть полягає в тому, що для елементів хеш-таблиці добавляється стан „вилучено”. Даний стан в процесі пошуку інтерпретується, як зайнято, а в процесі запису як вільно.

Тепер можна сформулювати алгоритми вставки, пошуку і вилучення для хеш-таблиці, яка має три стани елементів.

Вставка:

1. i = 0

2. a = h(key) + i*c

3. Якщо t(a) = вільно або t(a) = вилучено, то t(a) = key, записати елемент і стоп

4. i = i + 1, перейти до кроку 2

Вилучення:

1. i = 0

2. a = h(key) + i*c

3. Якщо t(a) = key, то t(a) = вилучено, стоп елемент вилучений

4. Якщо t(a) = вільно, то стоп елемент не знайдено

5. i = i + 1, перейти до кроку 2

Пошук:

1. i = 0

2. a = h(key) + i*c

3. Якщо t(a) = key, то стоп – елемент знайдено

4. Якщо t(a) = свободно, то стоп – елемент не знайдено

5. i = i + 1, перейти до кроку 2

Алгоритм пошуку для хеш-таблиці, яка має три стани, практично не відрізняється від алгоритму пошуку без врахування вилучення. Різниця полягає в тому, що при організації самої таблиці необхідно відмічати вільні і вилучені елементи. Це можна зробити, зарезервувавши два значення ключового поля. Інший варіант реалізації може передбачати введення додаткового поля, в якому фіксується стан елемента. Довжина такого поля може складати всього два біти, що достатньо для фіксації одного з трьох станів.

50.Організація даних для пошуку.
До тепер розглядалися способи пошуку в таблиці за ключами, які дозволяють однозначно ідентифікувати запис. Такі ключі називають первинними ключами. Можливий варіант організації таблиці, при якому окремий ключ не дозволяє однозначно ідентифікувати запис. Така ситуація часто зустрічається в базах даних. Ідентифікація запису здійснюється за деякою сукупністю ключів. Ключі, які не дозволяють однозначно ідентифікувати запис в таблиці, називаються вторинними ключами.

Навіть при наявності первинного ключа, для пошуку запису можуть використовуватися вторинні. Наприклад, пошукові системи Internet часто організовані як набори записів, які відповідають Web-сторінкам. В якості вторинних ключів для пошуку виступають ключові слова, а сама задача пошуку зводиться до вибірки з таблиці деякої множини записів, які містять потрібні вторинні ключі.

51.Метод часткових цілей.
Цей метод полягає у тому, що глобальна велика задача ділиться (якщо це можливо) на окремі задачі. Якщо велику задачу, можливо, і не можна осягнути, зрозуміти, як її розв’язувати, то для кожної з поділених задач може існувати давно відомий алгоритм розв’язку, або пошук такого алгоритму є значно легшою задачею.

Наприклад задача сортування масиву прямим обміном. Алгоритм сортування зводиться до відшукання мінімуму у несортованій частині масиву та дописування його до сортованої частини.

Функція пошуку проекції точки на площину зводиться до двох:

• пошуку рівняння прямої, перпендикулярної площині та такої, що проходить через задану точку;

• пошуку точки перетину перпендикуляру та площини.

Щоб знайти довжину перпендикуляру від точки до прямої, тобто відстань від прямої до площини, слід після знаходження проекції точки на площину звернутися до функції пошуку відстані між двома точками.

Останній приклад показує, що існують випадки, коли розбиття задачі на частинні задачі може призвести до зайвого ускладнення алгоритму, збільшення часу його роботи. Відстань від площини до точки шукається за допомогою канонічного рівняння площини, якщо у нього підставити координати точки, „за одну дію”. Але метод частинних цілей дає добре структурований, часто більш наочний алгоритм, тому кожного разу треба окремо вирішувати, яким шляхом іти.

Ще один класичний приклад методу частинних цілей – „Ханойська вежа”.

Принц Шак’я-Муні (623-544 р.р. до Р.Хр.), якого ще називали Буддою, що означає „просвітлений”, під час одної з своїх подорожей заснував у Ханої (В’єтнам) монастир. У головному храмі монастиря стоїть три стержні. На одну з них Будда надягнув 64 дерев’яні диски, усі різного діаметру, причому найширший поклав униз, а решту впорядкував за зменшенням розміру.

Слід переставити піраміду з осі A на вісь C у тому ж порядку, користуючись віссю B, як допоміжною, та додержуючись наступних правил:

• за один хід переставляти лише один диск з одної осі на іншу, а не декілька;

• забороняється класти більший диск на менший, тобто впорядкованість на кожній осі має зберігатися.

Ченці монастиря перекладають, не зупиняючись ні на мить, щосекунди по одному диску й досі. Коли піраміду буде складено на осі C, наступить кінець світу.

Рекурсивний підхід до програмування можна застосувати, якщо розуміти вежу з n дисків, як вежу з n-1 диску, що стоїть ще на одному. Щоби переставити всю піраміду з A на C, слід n-1 - піраміду переставити з A на B, перекласти один – найбільший – диск з A на C, а потім n-1 - піраміду з B на C. Таким чином, якщо за дрібнішу задачу править та ж задача, тільки з меншим значенням параметрів, то ця форма алгоритму частинних цілей є рекурсивним алгоритмом.

Як переставити вежу з двох дисків з A на C?

• переставити диск з A на B;

• переставити диск з A на C;

• переставити диск з B на C.

Повністю аналогічно, анітрохи не складніше, програмується повний алгоритм.

Щоби переставити вежу з n дисків (позначимо її B(n)) з A на C, слід:

• B(n-1) переставити з A на B;

• B(1) перекласти з A на C;

• B(n-1) переставити з B на C;

Тому основна функція буде void Move (int n, int from, int to), де n – розмір піраміди (якщо n = 1, то це лише один диск); from, to – осі, між якими відбувається операція пересування.

Для програмування слід визначити множину осей. Нам треба буде їх назви виводити на друк, тому назвемо їх 1, 2, 3. Крім того, треба за двома заданими осями вміти визначати третю, щоб її використовувати як робочу. Це легко зробити за допомогою оператора:

third = 6 - from - to;

Результатом роботи програми при n = 1 будемо вважати виведення рядка тексту на екран:

„Переставити диск з... на...”.

Тепер програма, яка писатиме ченцям інструкцію на 600 мільярдів років наперед, матиме вигляд:

#include < iostream.h>

#define n 64

void Move(int, int, int);

void main(void)

{

Move (n, 1, 3); // Переставити піраміду з n дисків з 1-ї осі на 3-ю

}

void Move(int n, int from, int to)

{

int third;

if (n == 1)

cout < < “Переставити диск з “ < < from < < “ на “ < < to < < endl;

else

{

third = 6 - from - to;

Move (n-1, from, third);

Move (1, from, to);

Move (n-1, third, to);

}

}

Усі рекурсивні алгоритми є реалізацією методу частинних цілей.

52.Метод динамічного програмування.
Нерідко не вдається поділити задачу на невелику кількість задач меншого розміру, об’єднання розв’язків яких дозволить отримати рішення початкової задачі. У таких випадках пробують поділити задачу на стільки задач, скільки необхідно, потім кожну поділену задачу ділять на ще декілька менших і так далі. Якщо б весь алгоритм зводився саме до такої послідовності дій, то в результаті отримали б алгоритм з експоненціальним часом виконання.

Але часто вдається отримати лише поліноміальну кількість задач меншого розміру і тому ту чи іншу задачу доводиться вирішувати багаторазово. Якщо б замість того відслідковувати рішення кожної вирішеної задачі і просто шукати у випадку необхідності відповідний розв’язок, то отримують алгоритм з поліноміальним часом виконання.

З точки зору реалізації, іноді, буває простіше створити таблицю розв’язків усіх задач меншого розміру, які доведеться вирішувати. Заповнюють таку таблицю незалежно від того, чи потрібна в реальному випадку конкретна задача для отримання загального розв’язку. Заповнення таблиці складових задач для отримання розв’язку певної задачі отримало назву динамічне програмування.

Динамічним програмуванням (в найбільш загальній формі) називають процес покрокового розв’язку задачі, коли на кожному кроці вибирається один розв’язок з множини допустимих на цьому кроці, причому такий, який оптимізує задану цільову функцію або функцію критерію. В основі теорії динамічного програмування лежить принцип оптимальності Белмана.

Форма алгоритму динамічного програмування може бути різною – спільною їх темою є лише заповнення таблиці і порядок заповнення її елементами.

53.Метод сходження.
Даний метод полягає у тому, щоби протягом пошуку найкращого розв’язку алгоритм відшукував все кращі та кращі варіанти розв’язку. Якщо ввести деяку кількісну оцінку якості розв’язку, який шукається, то такий метод подібний на здолання все нової та нової висоти при сходженні на вершину.

Розглянемо як приклад задачу про мандрівного крамаря. Крамар має проїхати n міст по циклу, використавши для цього цикл найменшої довжини та побувавши у кожному місті по одному разу.

Розв’язок можна шукати різними шляхами. Але самим очевидним є відшукати спочатку просто який-небудь цикл, що може вважатися „хорошим”. Для цього, наприклад, можна з першого міста їхати у найближче, звідти – у найближче з тих, що залишилися і так далі. З останнього міста треба буде повернутися назад. Це – перша вершина. Далі можна спробувати поліпшити цей варіант. Якщо це вийде, то це буде нова висота. Найкоротший цикл шукається за допомогою досить складних алгоритмів.

Ще один приклад використання методу сходження – ітерації.

Знайти значення корінь квадратний для довільного дійсного x – u = sqrt(x).

Якщо u = sqrt(x), то x/u = u;

Якщо u < sqrt(x), то x/u > sqrt(x).

Тому будь-коли середнє між u та x/u ближче до sqrt(x), ніж u. Тому, почавши з будь-якого „близького” початкового значення u(0), можна поступово поліпшувати наближення: u(n+1): = (u(n) + x / u(n)) / 2 доти, поки не буде виконуватися умова |u(n)- x / u(n)| < eps.

Даний тип алгоритмів має ще одну назву – „скупі” алгоритми. На кожній окремій стадії „скупий” алгоритм вибирає той варіант, який є локально оптимальним в тому чи іншому змісті. Раніше вже були розглянуті різні „скупі” алгоритми – алгоритм побудови найкоротшого шляху Дейкестри і алгоритм побудови стовбурного дерева мінімальної вартості Крускала. Алгоритм найкоротшого шляху Дейкестри є „скупим” у тому розумінні, що він вибирає вершину, найближчу до джерела, серед тих, найкоротший шлях яких ще невідомий. Алгоритм Крускала також „скупий” – він вибирає із ребер, які залишилися і не створюють цикл, ребро з мінімальною вартістю.

Потрібно зауважити, що не кожний „скупий” алгоритм дозволяє отримати оптимальний результат в цілому. Як це буває у житті, „скупа стратегія” у більшості випадків забезпечує локальний оптимум, у той же час як в цілому результат буде неоптимальним.

Узагальнюючи вище сказане, можна зробити висновок – стратегія методу полягає в тому, щоб почати з випадкового рішення і потім робити послідовні наближення. Почавши з випадково вибраного рішення, алгоритм робить випадковий вибір. Якщо нове рішення краще попереднього, програма закріплює зміни і продовжує перевірку інших випадкових змін. Якщо зміна не покращує рішення, програма відкидає його і робить нову спробу.

54.Дерева розв’язків.
Багато складних реальних задач можна змоделювати за допомогою дерев розв’язків. Кожний вузол дерева представляє один крок вирішення задачі. Кожна гілка в дереві представляє розв’язок, який веде до більш повного рішення. Листки є остаточним розв’язком. Мета полягає в тому, щоб знайти „найкращий шлях” від кореня дерева до листка при виконанні певних умов. Ці умови і значення поняття „найкращий” для шляху залежить від конкретної задачі.

Стратегію настільних ігор, таких як шахи, шашки, або „хрестики-нулики” можна змоделювати за допомогою дерев гри. Якщо в який-небудь момент гри існує 30 можливих ходів, то відповідний вузол у дереві гри матиме 30 гілок. Наприклад, для гри в „хрестики-нулики” кореневий вузол відповідає початковій позиції, при якій дошка порожня. Перший гравець може помістити хрестик в будь-яку з дев’яти кліток дошки. Кожному з цих дев’яти можливих ходів відповідає гілка дерева, яка виходить з кореня. Дев’ять вузлів на кінці цих гілок відповідають дев’яти різним позиціям після першого ходу гравця.

Після того, як перший гравець зробив хід, другий може поставити нулик в будь-яку з восьми кліток, що залишилися. Кожному з цих ходів відповідає гілка, що виходить з вузла, який відповідає поточній позиції.

Як можна здогадатися, дерево гри навіть для такої простої гри росте дуже швидко. Якщо воно буде продовжувати рости таким чином, що кожний наступний вузол в дереві матиме на одну гілку менше попереднього, то повне дерево гри матиме 9! = 362880 листки. Тобто, в дереві буде 362880 можливих шляхів розв’язку, які відповідають можливим варіантам гри.

Насправді багато з вузлів дерева в реальній грі будуть відсутніми, оскільки відповідні їм ходи заборонені правилами гри. Якщо гравець, що ходив першим, за три свої ходи поставить хрестики у верхній лівій, верхній середній і верхній правій клітках, то він виграє і гра закінчиться. Вузол, який відповідає цій позиції, не матиме нащадків, оскільки гра завершується на цьому кроці.

Після вилучення всіх неможливих вузлів в дереві залишається біля четверті мільйона листків. Це все ще дуже велике дерево, і пошук у ньому оптимального розв’язку методом повного перебору займає достатньо багато часу. Можна ще скоротити розмір цього дерева, враховуючи симетричність деяких позиція, але це підходить лише для конкретної гри. Для складніших ігор, таких як шашки, шахи або го, дерева мають величезний розмір. Якби під час кожного ходу в шахах гравець мав би 16 можливих варіантів, то дерево гри мало б більше трильйона вузлів після п’яти ходів кожного з гравців.

55.Програмування з поверненням назад.
Іноді доводиться мати справу з задачами пошуку оптимального розв’язку, коли неможливо застосувати жоден з відомих алгоритмів, які здатні допомогти відшукати оптимальний варіант розв’язку, і залишається застосувати останній засіб – повний перебір
. Реалізація пошуку з поверненням

Приведемо алгоритм побудови загального алгоритму пошуку з поверненням. Нехай задані правила деякої гри, тобто допустимі ходи і правила її завершення. Потрібно побудувати дерево цієї гри і оцінити його корінь. Це дерево можна побудувати звичним чином, а потім виконати обхід його вузлів у зворотному порядку. Такий обхід у зворотному порядку гарантує, що алгоритм попадає у внутрішній вузол лише після обходу всіх його нащадків, в результаті чого можна оцінити цей вузол, знайшовши максимум або мінімум значень його усіх нащадків.

Об’єм пам’яті для зберігання такого дерева може виявитися достатньо великим, але, якщо дотримуватися мір безпеки, можна обійтися зберіганням в пам’яті в будь-який заданий момент часу лише одного шляху – від кореня до того чи іншого вузла. Приведемо алгоритм пошуку, який виконує обхід дерева за допомогою послідовності рекурсивних викликів. Цей алгоритм передбачає виконання наступних умов:

• Виграші є дійсними числами з обмеженого інтервалу, наприклад [-1, 1].

• Константа більша, ніж будь-який додатній виграш, а - менша, ніж будь-який від’ємний виграш.

• Дані типу modetype (тип режиму) можуть приймати два фіксовані значення – MIN, або MAX.

• Передбачений тип даних boardtype (тип ігрової дошки), яка визначається способом представлення позицій на дошці.

• Передбачена функція payoff (виграш), яка обчислює виграш для будь-якої позиції, яка є листком дерева.

float Search(boardtype B, modetype mode)

// Оцінює і повертає виграш для позиції В з передбачення,

// що наступним повинен ходити гравець 1 (mode=MAX) або гравець 2 (mode=MIN)

{

boardtype C; // нащадок позиції В

float Value; // тимчасове значення виграшу

if (B є листком) // 1

return payoff(B); // 2

else

{

if (mode==MAX) // 3

Value = -; // 4

Else

Value =; // 5

For (для кожного сина С позиції В) // 6

{

if (mode==MAX) // 7

Value = max(Value, Search(C, MIN)); // 8

Else

Value = min(Value, Search(C, MAX)); // 9

return Value; // 10

}

}

}

60. Евристичні алгоритми.

У складніших іграх практично неможливо провести пошук навіть в невеликому фрагменту дерева. У цих випадках, можна використовувати різні евристики. Евристикою називається алгоритм або емпіричне правило, яке ймовірно, але не обов’язково дасть добрий результат.

Наприклад, в шахах звичайною евристикою є „посилення переваги”. Якщо у супротивника менше сильних фігур і однакова кількість інших, то слід йти на розмін при кожній нагоді. Зменшення кількості фігур робить дерево рішень коротшим і може збільшити відносну перевагу. Ця стратегія не гарантує виграшу, але підвищує його вірогідність.

Інша евристика, що часто використовується, полягає в присвоєнні різних ваг різним клітинкам. У шахах вага кліток в центрі дошки вища, оскільки фігури, що знаходяться на цих позиціях, можуть атакувати більшу частину дошки. Коли обчислюється вага поточної позиції на дошці, вона може присвоюватися більшою фігурам, які займають клітки в центрі дошки.

Якщо якість рішення не так важлива, то прийнятним може бути результат, отриманий за допомогою евристики. В деяких випадках точність вхідних даних може бути недостатньою. Тоді хороше евристичне рішення може бути таким же правильним, як і теоретично „якнайкраще рішення”.

У попередньому прикладі метод гілок і границь використовувався для вибору інвестиційних можливостей. Проте, вкладення можуть бути ризикованими, і точні результати часто наперед невідомі. Можливо, що наперед буде невідомий точний дохід або навіть вартість деяких інвестицій. В цьому випадку, ефективне евристичне рішення може бути таким же надійним, як і якнайкраще рішення, яке ви може обчислити точно.

Отже, евристичні алгоритми – це алгоритми, які мають такі властивості:

• Вони дозволяють знайти добрі, хоча і не завжди найкращі розв’язки з усіх, що існують.

• Метод пошуку або побудови розв’язку звичайно значно простіший, ніж той що гарантує оптимальність розв’язку.

Поняття „добрий розв’язок” змінюється від задачі до задачі, тому його важко визначити точно. Припустимість використання евристики залежить від співвідношення часу та складності пошуку розв’язку обома способами та співвідношення якості обох розв’язків.

У цьому розумінні усі умови, що висуваються до розв’язку, звичайно ділять на дві групи щодо витрат праці:

• ті, які легко задовольнити;

• ті, що вимагають великої роботи.

З іншої сторони, вони поділяються на такі групи щодо їхньої важливості для кінцевої якості:

• ті, які обов’язково слід задовольнити;

• ті, що можуть бути послаблені або змінені.

Цю ситуацію образно показано в таблиці

Повернемося до нашого прикладу – задачі про мандрівного крамаря. Якщо міст, про які йдеться – багато, то пошук точно мінімального за довжиною циклу може вимагати дуже багато часу. З іншої сторони, об’їзд слід зробити лише один раз. Якщо витрати на пошук оптимального маршруту можуть виявитися більшими або еквівалентними до витрат на пальне під час подорожі, то, можливо, варто просто рушати в путь, прямуючи до найближчого міста кожного разу.

Якщо ж слід відшукати найкращий маршрут для регулярного об’їзду (наприклад, вибирання пошти зі скриньок, розвезення хлібу з заводу по магазинах, маршрут для руки-маніпулятора робота під час монтування друкованих плат), то все ж варто відшукати оптимальний маршрут, бо витрати на програмування є разовими, а витрати на зайвий рух є регулярними.

Візьмемо за приклад сортування масиву. Якщо потрібно відсортувати один раз масив зі 100 записів, то можна використати будь-який з простих методів сортування – на весь процес буде витрачено щонайбільше 2-3 секунди машинного часу. Якщо ж розробляють пакет, що буде регулярно сортувати значні масиви інформації, то варто написати сучасну програму.

Частіше за все евристичні алгоритми базуються на методі сходження або на методі частинних цілей.