
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритми обходу дерева.
|
|
Бінарне дерево можна обходити трьома основними способами: низхідним, змішаним і висхідним
Схемно алгоритм обходу бінарного дерева відповідно до низхідного способу може виглядати таким чином:
1. В якості чергової вершини взяти корінь дерева. Перейти до пункту 2.
2. Провести обробку чергової вершини відповідно до вимог задачі. Перейти до пункту 3.
3.а) Якщо чергова вершина має обидві гілки, то в якості нової вершини вибрати ту вершину, на яку посилається ліва гілка, а вершину, на яку посилається права гілка, занести в стек; перейти до пункту 2;
3.б) якщо чергова вершина є кінцевою, то вибрати в якості нової чергової вершини вершину із стека, якщо він не порожній, і перейти до пункту 2; якщо ж стек порожній, то це означає, що обхід всього дерева закінчений, перейти до пункту 4;
3.в) якщо чергова вершина має тільки одну гілку, то в якості чергової вершини вибрати ту вершину, на яку ця гілка вказує, перейти до пункту 2.
4. Кінець алгоритму.
Змішаний обхід можна описати таким чином:
1) Спуститися по лівій гілці із запам’ятовуванням вершин в стеку;
2) Якщо стек порожній те перейти до п.5;
3) Вибрати вершину із стеку і обробити дані вершини;
4) Якщо вершина має правого сина, то перейти до нього; перейти до п.1.
5) Кінець алгоритму.
Рекурсивний змішаний обхід описується таким чином:
1) Змішаний обхід лівого піддерева;
2) Обробка кореневої вершини;
3) Змішаний обхід правого піддерева.
Алгоритм висхідного обходу можна представити таким чином:
1) Спуститися по лівій гілці із запам’ятовуванням вершини в стеку як 1-й вид стекових записів;
2) Якщо стек порожній, то перейти до п.5;
3) Вибрати вершину із стека, якщо це перший вид стекових записів, то повернути його в стек як 2-й вид стекових записів; перейти до правого сина; перейти до п.1, інакше перейти до п.4;
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
4) Обробити дані вершини і перейти до п.2;
5) Кінець алгоритму.
Принципи формалізації алгоритмів.
Перші спроби уточнення поняття алгоритму та його дослідження здійснювали в першій половині XX століття Алан Тюринг, Еміль Пост, Жак Ербран, Курт Гедель, Андрій Марков, Алонзо Черч. Було розроблено декілька означень поняття алгоритму, але згодом було з'ясовано, що всі вони визначають одне й те саме поняття.
Часткова формалізація поняття алгоритму почалася зі спроб вирішення проблеми дозволу (нім. Проблема дозволу), яку сформулював Давид Гільберт в 1928 році. Наступні етапи формалізації були необхідні для визначення ефективних обчислень або «ефективного методу»; серед таких формалізацій - рекурсивні функції Геделя - Ербрана - Кліні 1930 1934 і 1935 рр, λ -числення Алонзо Черча 1936 р «1 Формулювання» Еміля Поста 1936 року і машина Тьюринга.. У методології алгоритм є базисним поняттям і отримує якісно нове поняття як оптимальності в міру наближення до прогнозованого абсолюту. У сучасному світі алгоритм в формалізованому виразі складає основу освіти на прикладах, за подобою.
Основні принципи формалізаціі:
Машина Тюринга
Рекурсивні функці
Нормальні алгоритми Маркова
Інші формалізації
Для деяких задач названі вище формалізми можуть ускладнювати пошук розв'язків та здійснення досліджень. Для подолання перешкод було розроблено як модифікації «класичних» схем, так і створено нові моделі алгоритму. Зокрема, можна назвати:
• багатострічкову та недетермінованHYPERLINK " https://uk.wikipedia.org/wiki/Недетермінована_машина_Тюрінга" у машина Тюрінга;
• регістровHYPERLINK " https://uk.wikipedia.org/w/index.php? title=Регістрова_машина& action=edit& redlink=1" у та РАМ-машинHYPERLINK " https://uk.wikipedia.org/wiki/РАМ-машина" у — прототип сучасних комп'ютеріHYPERLINK " https://uk.wikipedia.org/wiki/Комп'ютер" в та віHYPERLINK " https://uk.wikipedia.org/wiki/Віртуальна_машина" ртуальних машин;
• Скінченні та клітинні автомати
Покрокове проектування алгоритмів.
Оскільки для вирішення вихідної задачі застосовують деяку математичну модель, то тим самим можна формалізувати алгоритм вирішення в термінах цієї моделі. У початкових версіях алгоритму часто застосовуються узагальнені оператори, які потім перевизначаться у вигляді більш дрібних, чітко визначених інструкцій.
В основу процесу проектування програми з розбиттям її на достатню кількість дрібних кроків можна покласти наступну послідовність дій:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
1.Вихідним станом процесу проектування є більш-менш точне формулювання мети алгоритму, або конкретніше – результату, який повинен бути отриманий при його виконанні. Формулювання проводиться на природній мові.
2.Проводиться збір фактів, які стосуються будь-яких характеристик алгоритму, і робиться спроба їх представлення засобами мови.
3.Створюється образна модель процесу, який відбувається, використовуються графічні та інші способи представлення, образні „картинки”, які дозволяють краще зрозуміти виконання алгоритму в динаміці.
4.В образній моделі виділяється найбільш суттєва частина, для якої підбирається найбільш точне словесне формулювання.
5.Проводиться визначення змінних, які необхідні для формального представлення даного кроку алгоритму.
6.Вибирається одна з конструкцій – проста послідовність дій, умовна конструкція або циклу. Складні частини вибраної формальної конструкції (умова, заголовок циклу) залишаються в словесному формулюванні.
Для інших неформалізованих частин алгоритму, які залишились у словесному формулюванні – перерахована послідовність дій повторюється.
Зовнішня сторона такого процесу проектування програми полягає в тому, що одне словесне формулювання алгоритму замінюється на одну з трьох можливих конструкцій мови, елементи якої продовжують залишатися в неформальному, словесному формулюванні. Насправді, кожне словесне формулювання алгоритму містить важливий перехід, який виконується в голові програміста і не може бути формалізованим – перехід від мети (результату) роботи програми до послідовності дій, які приводять до потрібного результату. Тобто алгоритм вже формулюється, але тільки з використанням образного мислення і природної мови.
Схематично узагальнений процес програмування можна представити наступною схемою.

Основні характеристики алгоритмів.
Охарактеризуємо поняття алгоритму не формально, а дескриптивно за допомогою таблиці:
| Вирішення гарантоване | |||
| Так | Ні | ||
| Чи обов’язкове оптимальне вирішення | Так | Алгоритм | Імовірнісний алгоритм |
| Ні | Приблизний алгоритм | Евристичний алгоритм |
Як бачимо, алгоритм – це механізм, який не тільки повинен гарантувати те, що вирішення колись буде знайдене, але й те, що буде знайдене саме оптимальне, тобто найкраще вирішення. Крім того, алгоритм повинен мати наступні п’ять якостей:
Обмеженість в часі – робота алгоритму обов’язково повинна завершитись через деякий розумний період часу.
Правильність – алгоритм повинен знаходити правильне, а не будь-яке рішення.
Детермінованість – скільки б разів не виконувався алгоритм з однаковими вхідними даними, результат повинен бути однаковим.
Скінченність – опис роботи алгоритму повинен мати скінчену кількість кроків.
Однозначність – кожний крок алгоритму повинен інтерпретуватися однозначно.
Як видно з таблиці, евристика – це пряма протилежність класичному алгоритму, так як вона не дає ніяких гарантій на те, що рішення буде знайдене, так само, як і на те, що воно буде оптимальним. Між ними є два перехідні стани, назв яким, на жаль, ще не придумали, і тому їх називають приблизними алгоритмами (рішення гарантоване, але його оптимальність – ні) і імовірнісні алгоритми (рішення не гарантоване, але якщо воно буде знайдене, то обов’язково буде оптимальним).
36.Поняття складності алгоритму.
У процесі вирішення прикладних задач вибір потрібного алгоритму викликає певні труднощі. І справді, на чому базувати свій вибір, якщо алгоритм повинен задовольняти наступні протиріччя.
1.Бути простим для розуміння, перекладу в програмний код і наладки.
2.Ефективно використовувати комп’ютерні ресурси і виконуватися швидко.
Якщо написана програма повинна виконуватися лише декілька разів, то перша вимога найбільш важлива. Якщо мати справу з задачею, вирішення якої потребує значних обчислювальних затрат, то вартість виконання програми може перевищити вартість написання програми, особливо якщо програма повинна виконуватися багаторазово. Тому, з економічної точки зору, перевагу буде мати складний комплексний алгоритм.
Існує декілька способів оцінки складності алгоритмів. Програмісти, звичайно, зосереджують увагу на швидкості алгоритму, але важливі й інші вимоги, наприклад, до розмірів пам’яті, вільного місця на диску або інших ресурсів. Від швидкого алгоритму може бути мало толку, якщо під нього буде потрібно більше пам’яті, ніж встановлено на комп’ютері.
Важливо розрізняти практичну складність, яка є точною мірою часу обчислення і об’єму пам’яті для конкретної моделі обчислювальної машини, і теоретичну складність, яка більш незалежна від практичних умов виконання алгоритму і дає порядок величини вартості.
Більшість алгоритмів надає вибір між швидкістю виконання і ресурсами. Задача може виконуватися швидше, використовуючи більше пам’яті, або навпаки – повільніше з меншим обсягом пам’яті.
37.Ефективність алгоритмів.
Одним із способів визначення часової ефективності алгоритмів полягає в наступному: на основі даного алгоритму потрібно написати програму і виміряти час її виконання на певному комп’ютері для вибраної множини вхідних даних. Хоча такий спосіб популярний і, безумовно, корисний, він породжує певні проблеми. Визначений час виконання програми залежить не тільки від використаного алгоритму, але й від архітектури і набору внутрішніх команд даного комп’ютера, Час виконання також може суттєво залежати від вибраної множини тестових вхідних даних. Ця залежність стає очевидною при реалізації одного й того ж алгоритму з використанням різних комп’ютерів. Щоб підвищити об’єктивність оцінки алгоритмів, учені, які працюють в галузі комп’ютерних наук, прийняли асимптотичну часову складність як основну міру ефективності виконання алгоритму.
Продуктивність алгоритму оцінюють за порядком величини. Говорять, що алгоритм має складність порядку 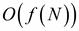 , якщо час виконання алгоритму росте пропорційно функції
, якщо час виконання алгоритму росте пропорційно функції  із збільшенням розмірності початкових даних
із збільшенням розмірності початкових даних  .
.  – позначає „величина порядку”.
– позначає „величина порядку”.
Оцінка з точністю до порядку дає верхню межу складності алгоритму. Те, що програма має певний порядок складності, не означає, що алгоритм буде дійсно виконуватися так довго. При певних вхідних даних, багато алгоритмів виконується набагато швидше, ніж можна припустити на підставі їхнього порядку складності.
Аналіз складності алгоритму корисний для розуміння особливостей алгоритму і звичайно знаходить частини програми, що витрачають велику частину комп’ютерного часу. Надавши увагу оптимізації коду в цих частинах, можна внести максимальний ефект в збільшення продуктивності програми в цілому.
Правила аналізу складності алгоритмів.
У загальному випадку час виконання оператора або групи операторів можна розглядати як функцію з параметрами – розміром вхідних даних і/або одної чи декількох змінних. Але для часу виконання програми в цілому допустимим параметром може бути лише розмір вхідних даних.
Час виконання операторів присвоєння, читання і запису звичайно має порядок  .
.
Час виконання послідовності операторів визначається за правилом сум. Тому міра росту часу виконання послідовності операторів без визначення констант пропорційності співпадає з найбільшим часом виконання оператора в даній послідовності.
Час виконання умовних операторів складається з часу виконання умовно виконуваних операторів і часу обчислення самого логічного виразу. Час обчислення логічного виразу часто має порядок  . Час для всієї конструкції if-then-else складається з часу обчислення логічного виразу і найбільшого з часів, який необхідний для виконання операторів, що виконуються при різних значеннях логічного виразу.
. Час для всієї конструкції if-then-else складається з часу обчислення логічного виразу і найбільшого з часів, який необхідний для виконання операторів, що виконуються при різних значеннях логічного виразу.
Час виконання циклу є сумою часів усіх часів виконуваних конструкцій циклу, які в свою чергу складаються з часів виконання операторів тіла циклу і часу обчислення умови завершення циклу (часто має порядок  ). Часто час виконання циклу обчислюється, нехтуючи визначенням констант пропорційності, як добуток кількості виконуваних операцій циклу на найбільший можливий час виконання тіла циклу. Час виконання кожного циклу, якщо в програмі їх декілька, повинен визначатися окремо.
). Часто час виконання циклу обчислюється, нехтуючи визначенням констант пропорційності, як добуток кількості виконуваних операцій циклу на найбільший можливий час виконання тіла циклу. Час виконання кожного циклу, якщо в програмі їх декілька, повинен визначатися окремо.
Постановка задачі сортування.
Для самого загального випадку сформулюємо задачу сортування таким чином: є деяка неврегульована вхідна множина ключів і потрібно отримати множину цих же ключів, впорядкованих за збільшенням або зменшенням в чисельному порядку.
Зі всіх задач програмування сортування, можливо, має найбагатший вибір алгоритмів розв’язку. Назвемо деякі чинники, які впливають на вибір алгоритму.
1.Наявний ресурс пам’яті: повинні вхідна й вихід множини розташовуватися в різних ділянках пам’яті.
2.Початкова впорядкованість вхідної множини: у вхідній множині можуть попадатися впорядковані ділянки.
3.Часові характеристики операцій: при визначенні порядку алгоритму час виконання вважається звичайно пропорційним кількості порівнянь ключів.
4.Складність алгоритму є не останнім міркуванням при його виборі.
Ефективність методів сортування визначається двома параметрами:
1.кількістю порівнянь;
2.кількістю пересилань елементів.
Класифікація алгоритмів сортування.
Різноманітність алгоритмів сортування вимагає деякої їхньої класифікації. Вибраний один з вживаних для класифікації підходів, орієнтований перш за все на логічні характеристики використовуваних алгоритмів. Згідно цьому підходу будь-який алгоритм сортування використовує одну з наступних чотирьох стратегій (або їхню комбінацію).
1.Стратегія вибірки. З вхідної множини вибирається наступний за критерієм впорядкованості елемент і включається в вихідну множину на місце, наступне за номером.
2.Стратегія включення. З вхідної множини вибирається наступний за номером елемент і включається в вихідну множину на те місце, яке він повинен займати відповідно до критерію впорядкованості.
3.Стратегія розподілу. Вхідна множина розбивається на ряд підмножин і сортування ведеться у середині кожної такої підмножини.
4.Стратегія злиття. Вихідна множина отримується шляхом злиття маленьких впорядкованих підмножин.
Також алгоритми класифікуються за:
• потреби у додатковій пам'яті або її відсутності
• потреби в знаннях про структуру даних, що виходять за рамки операції порівняння, або відсутності такої
41.Сортування вибіркою.
Даний метод реалізує практично „дослівно” стратегію вибірки. При програмній реалізації алгоритму виникає проблема значення ключа „порожньо”. Досить часто програмісти використовують в якості такого деяке явно відсутнє у вхідній послідовності значення ключа. Інший підхід – створення окремого вектора, кожний елемент якого має логічний тип і відображає стан відповідного елемента вхідної множини.
Сортування вибором — простий алгоритм сортування лінійного масиву, на основі вставок. Має ефективність n2, що робить його неефективним при сортування великих масивів, і в цілому, менш ефективним за подібний алгоритм сортування включенням. Сортування вибором вирізняється більшою простотою, ніж сортування включенням, і в деяких випадках, вищою продуктивністю.
Алгоритм працює таким чином:
1.Знаходить у списку найменше значення
2.Міняє його місцями із першим значеннями у списку
3.Повторює два попередніх кроки, доки список не завершиться (починаючи з другої позиції)
4.Фактично, таким чином ми поділили список на дві частини: перша (ліва) — повністю відсортована, а друга (права) — ні.
Ось приклад сортування масиву з п'яти елементів за даним алгоритмом:
64 25 12 22 11
11 25 12 22 64
11 12 25 22 64
11 12 22 25 64
Алгоритм сортування простою вибіркою рідко застосовується. Набагато частіше застосовується його обмінний варіант.
Сортування вибором не є складним в аналізі та порівнянні його з іншими алгоритмами, оскільки жоден з циклів не залежить від даних у списку. Знаходження найменшого елементу вимагає перегляду усіх n елементів (у цьому випадку n − 1 порівняння), і після цього, перестановки його до першої позиції.
Приведені вище алгоритми сортування вибіркою практично нечутливі до початкової впорядкованості. В будь-якому випадку пошук мінімуму вимагає повного перегляду вхідної множини. В обмінному варіанті початкова впорядкованість може дати деяку економію на перестановках для випадків, коли мінімальний елемент знайдений на першому місці у вхідній множині.
|
|
