Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача, содержащая в целевой функции и правой части ограничений параметр

Пример 3.3.1. Для всех значений параметра найти максимальное значение функции

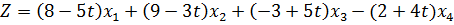
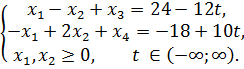
Решение. Пусть 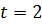. Находим симплекс-методом решение задачи.

Таблица 3.3.1.

БП	СЧ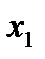
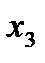
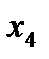
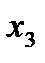
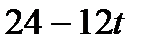
			-1
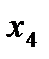
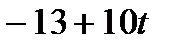
		-1
С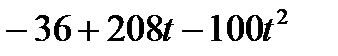

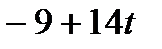
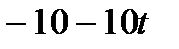
Таблица 3.3.2.

БП	СЧ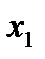
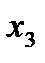
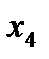
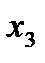
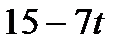
		1/2			1/2
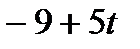
		-1/2			1/2
С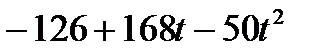

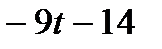
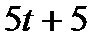
План 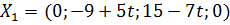оптимален при условии

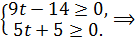
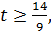
а среди компонент вектора 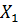нет отрицательных чисел:

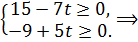
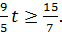
Следовательно, при , ,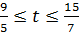

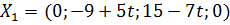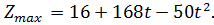
Если 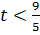, то 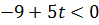и вектор 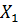не является планом задачи. Переходим к новой таблице, применяя двойственный симплекс-метод:

Таблица 3.3.3.

БП	СЧ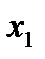
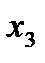
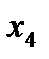
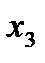
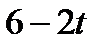
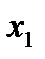
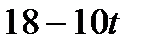
			-2		-1
С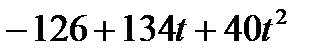

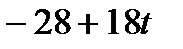
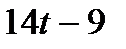
Вектор 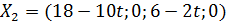оптимален при условии

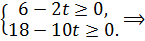
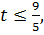
то есть при , .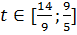

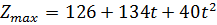Если 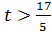, то из симплексной таблицы 3.3.2 следует, что задача не имеет решения, так как в строке 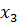нет отрицательных чисел.

Мы рассмотрели интервал 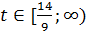. Пусть 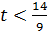, тогда переходим к новому оптимальному плану:

Таблица 3.3.4.

БП	СЧ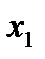
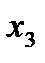
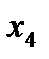
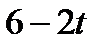
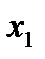
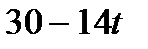
С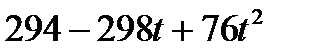

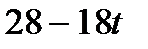
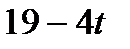
Таким образом, при ,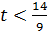

.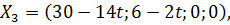
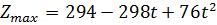