Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача, содержащая в целевой функции параметр

Предположим, что коэффициенты линейной функции 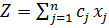могут изменяться в некоторых допустимых пределах 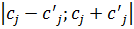, тогда для удобства исследования коэффициенты линейной функции можно заменить выражением 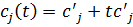, где 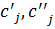– постоянные, а – параметр, изменяющийся в некоторых пределах. В этом случае математическая задача может быть поставлена следующим образом.

Дана линейная функция

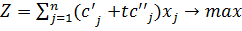(3.1.1)

и система линейных ограничений

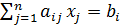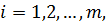, (3.1.2)

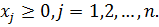
Считая значение параметра равным некоторому числу 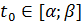, находим симплексным методом или методом искусственного базиса решение, полученной таким образом задачи линейного программирования.

В результате при данном значении 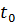либо найдем оптимальный план задачи, либо установим ее неразрешимость. В первом случае, используя элементы 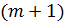– й строки последней симплекс - таблицы решения задачи, в которой записаны числа 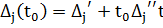, находим:

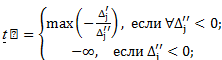
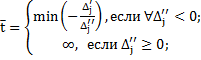
Для всех задача имеет один и тот же оптимальный план, что и при .

В том случае, если задача при 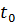неразрешима, 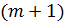– в строке последней симплекс - таблицы ее решения имеется число 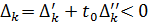, где 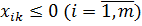. Тогда:

1) если 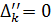, то задача неразрешима для любого ;

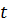2) если 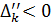, то задача неразрешима для всех ;

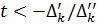3) если 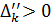, то задача неразрешима для всех .

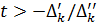Определив все значения параметра 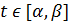, для которых задача имеет один и тот же оптимальный план или для которых задача неразрешима, получаем промежуток изменения параметра 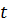, который исключаем из рассмотрения. Снова полагаем значение параметра 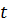равным некоторому числу, принадлежащему промежутку, и находим решение полученной задачи.

После каждой итерации определяется либо промежуток, в котором для всех значений параметра задача имеет один и тот же оптимальный план, либо промежуток, в котором для всех значений параметра задача не имеет решения.

Процесс нахождения решения задачи включает следующие этапы:

1. Считая значение параметра 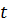равным некоторому числу 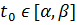, находят оптимальный план 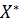или устанавливают неразрешимость полученной задачи линейного программирования.

2. Определяют множество значений параметра 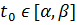, для которых найденный оптимальный план является оптимальным или задача неразрешима. Эти значения параметра исключают из рассмотрения.

3. Полагают значения параметра 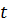равным некоторому числу, принадлежащему оставшейся части промежутка 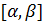, и находят решение полученной задачи линейного программирования.

4. Определяют множество значений параметра 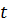, для которых новый оптимальный план остается оптимальным или задача неразрешима. Вычисления повторяют до тех пор, пока не будут исследованы все значения параметра .

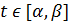Пример 3.1.1. Для всех значений параметра 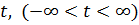найти максимальное значение функции

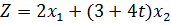
при условиях:

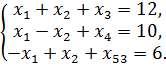
Решение. Возьмем (число 0 выбрано произвольно) и найдем симплекс-методом оптимальный план.

Таблица 3.1.1.

БП	СЧ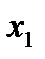
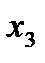
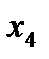
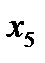
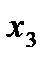
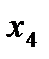
			-1
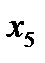
		-1
С		-2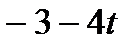

Таблица 3.1.2.

БП	СЧ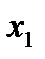
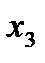
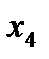
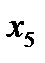
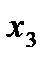
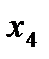
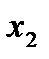
		-1
С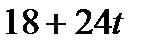

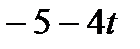
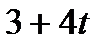
Таблица 3.1.3.

БП	СЧ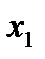
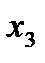
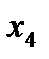
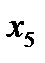
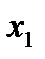
				1/2		-1/2
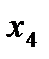
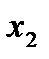
				1/2		1/2
С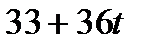

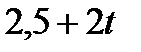
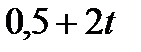
Определим значения 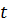, при которых план, соответствующий таблице 3.1.3, останется оптимальным:

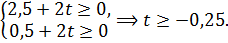
Следовательно, при 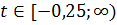задача имеет оптимальное решение: 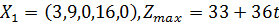. Возьмем 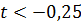. Тогда столбец 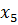– разрешающий. Переходим к новому опорному плану:

Таблица 3.1.4.

БП	СЧ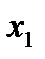
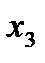
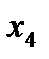
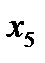
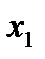
				1/2	1/2
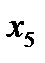
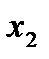
				1/2	-1/2
С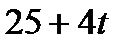

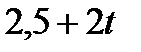
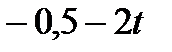
Этот план оптимален при условии:

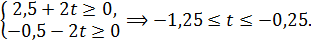
Следовательно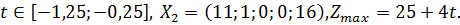, при При 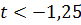имеем:

Таблица 3.1.5.

БП	СЧ
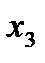
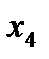
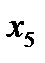
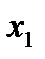
			-1
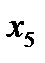
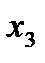
					-1
С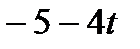

Этот план оптимален при условии: 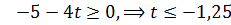. Следовательно, при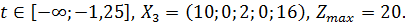