Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача, содержащая в свободных членах системы ограничений параметр

Дана линейная функция и система линейных ограничений

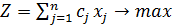(3.2.1)

(3.2.2)

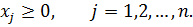
Алгоритм решения задачи (3.2.1)-(3.2.2) подобен рассмотренному выше алгоритму решения задачи (3.1.1)-(3.1.2). Полагая значение параметра 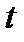равным некоторому числу 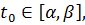находим решение полученной задачи линейного программирования. При данном значении параметра 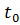, либо определяем оптимальный план задачи, либо установим ее неразрешимость. В первом случае найденный план является оптимальным для любого 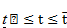, где

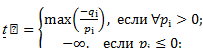
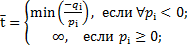
и числа 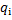и 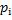определены компонентами оптимального плана и зависят от :

.

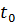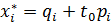Если при 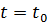задача (3.2.1) - (3.2.2) неразрешима, то либо целевая функция задачи (3.2.1) не ограничена на множестве планов, либо система уравнений (3.2.2) не имеет неотрицательных решений. В первом случае задача неразрешима для всех 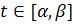, а во втором случае определяем все значения параметра 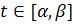, для которых система уравнений (3.2.2) несовместна, и исключаем их из рассмотрения. После определения промежутка, в котором задача (3.2.1) - 3.2.2) имеет один и тот же оптимальный план или неразрешима, выбираем новое значение параметра 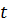, не принадлежащее найденному промежутку, и находим решение полученной задачи линейного программирования. При этом решение новой задачи ищем с помощью двойственного симплекс-метода. Продолжая итерационный процесс, после конечного числа шагов получаем решение задачи (3.2.1) - (3.2.2). Итак, процесс нахождения решения задачи (3.2.1) - (3.2.2) включает следующие основные этапы:

1. Считая значение параметра 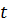равным некоторому числу 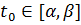, находят оптимальный план или устанавливают неразрешимость полученной задачи линейного программирования.

2. Находят значения параметра 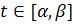, для которых задача (3.2.1) - (3.2.2) имеет один и тот же оптимальный план или неразрешима. Эти значения параметра исключают из рассмотрения.

3. Выбирают значения параметра 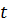из оставшейся части промежутка 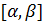и устанавливают возможность определения нового оптимального плана. В случае существования оптимального плана находят его двойственным симплекс-методом.

4. Определяют множество значений параметра 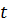, для которых задача имеет один и тот же новый оптимальный план или неразрешима. Вычисления проводят до тех пор, пока не будут исследованы все значения параметра .

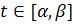Пример 3.2.1. Для каждого значения параметра найти максимальное значение функции

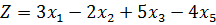
Решение. Считая 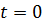, находим решение:

Таблица 3.2.1.

БП	СЧ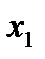
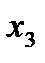
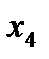
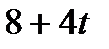
			-1
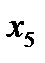
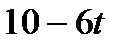
		-2
С		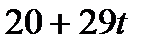	-1

Таблица 3.2.2.

БП	СЧ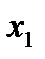
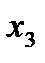
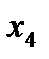
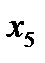
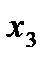
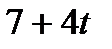
						-1/2
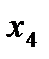
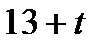
						1/2
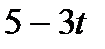
		-1				1/2
С		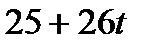				1/2

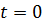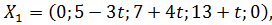
Оптимальный план при : 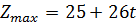. Этот план будет оставаться оптимальным, пока среди его компонент не окажется отрицательного числа:

.

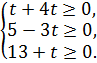
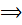
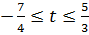Следовательно, при 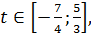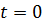: 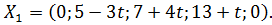Исследуем, имеет ли задача оптимальные планы при 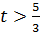. Если 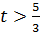, то 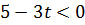и, следовательно, 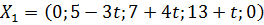не является планом задачи. Поэтому надо перейти к новому плану. Это можно сделать, когда в строке 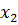имеются отрицательные числа. В данном случае это условие выполняется. Переходим к оптимальному плану, применяя двойственный симплекс-метод.

Таблица 3.2.3.

БП	СЧ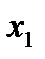
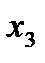
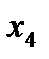
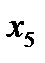
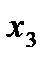
						1/2
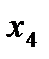
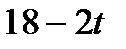
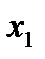
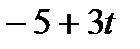
			-1			-1/2
С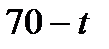

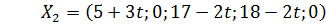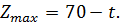, Этот план остается оптимальным при

.

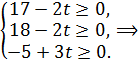
Если 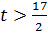, то это решение не является планом, так как
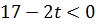. Так как в строке 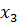нет отрицательных чисел, то исходная задача неразрешима.

При 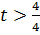, 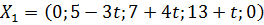не является планом, так как . С помощью таблицы 3.2.2 переходим к следующему решению:

Таблица 3.2.4.

БП	СЧ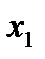
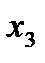
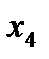
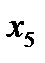
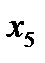
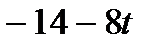
		-4		-2
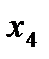
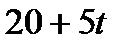
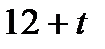
С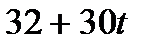

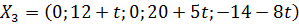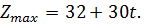, Этот план оптимален при услови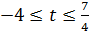и . При 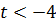задача неразрешима, так как в строке 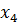нет отрицательных чисел.