
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава I.
|
|
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Основные понятия и определения
Стандартной задачей линейного программирования будем называть задачу, которая состоит в нахождении экстремума функции
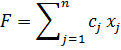 (1)
(1)
при условиях
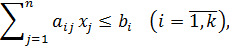 (2)
(2)
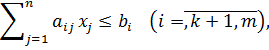 (3)
(3)
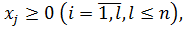 (4)
(4)
где 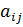 ,
, 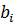 ,
, 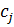 – заданные константы и
– заданные константы и 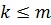 .
.
Функция 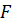 называется целевой функцией задачи (1) – (4), а условия (2) – (4) – система ограничений данной задачи.
называется целевой функцией задачи (1) – (4), а условия (2) – (4) – система ограничений данной задачи.
Симметричной задачей линейного программирования называется задача, которая заключается в нахождении экстремума функции 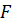 при выполнении условий (2) и (4), где
при выполнении условий (2) и (4), где 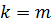 ,
, 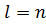 .
.
Канонической задачей линейного программирования называется задача, которая заключается в нахождении экстремума функции 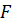 при выполнении условий (3) и (4), где
при выполнении условий (3) и (4), где 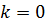 ,
, 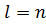 .
.
Множество чисел, 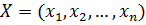 удовлетворяющих условиям задачи (2) – (4), называется допустимым решением или планом.
удовлетворяющих условиям задачи (2) – (4), называется допустимым решением или планом.
План 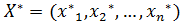 , при котором целевая функция задачи достигает своего экстремума, называется оптимальным.
, при котором целевая функция задачи достигает своего экстремума, называется оптимальным.
Значение целевой функции 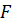 при плане
при плане 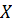 будем обозначать через
будем обозначать через  . Таким образом,
. Таким образом, 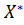 – оптимальное решение задачи, если для произвольного
– оптимальное решение задачи, если для произвольного 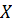 выполняется неравенство
выполняется неравенство
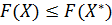 [соответственно
[соответственно 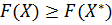 ].
].
Любые из трех показанных выше задач эквиваленты, то есть каждую можно переписать в другую форму задачи, с помощью простых действий. Если есть метод определения одной из данных задач, то тем самым может быть найден оптимальный план каждой из трех задач.
Дабы перейти от одной формы записи задачи линейного программирования к другой, нужно умение, во-первых, привести задачу поиска минимума функции к задаче поиска максимума; во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот; в-третьих, замещать переменные, которые не подчинены условию неотрицательности.
В том случае, когда нужно найти минимум функции 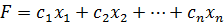 , можно перейти к отысканию максимума функции
, можно перейти к отысканию максимума функции
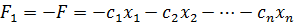 , так как
, так как 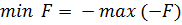 .
.
Ограничение-неравенство начальной задачи линейного программирования, имеющее вид «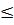 », можно преобразовывать в ограничение-равенство путем прибавления к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида «
», можно преобразовывать в ограничение-равенство путем прибавления к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида «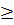 » – в ограничение-равенство путем вычитания из его левой части дополнительной неотрицательной переменной. Значит, ограничение-неравенство
» – в ограничение-равенство путем вычитания из его левой части дополнительной неотрицательной переменной. Значит, ограничение-неравенство
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
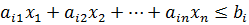
преобразуется в ограничение-равенство
 , (5)
, (5)
а ограничение-неравенство
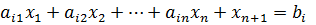 – в ограничение-равенство
– в ограничение-равенство
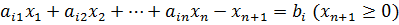 (6)
(6)
В это время любое уравнение системы ограничений
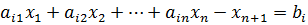
можно переписать в виде неравенств:
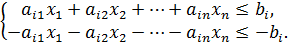 (7)
(7)
Дополнительные неотрицательные переменные, при преобразовании ограничений-неравенств в ограничения-равенства, их количество становится равным количеству преобразуемых неравенств. Частично включаемые дополнительные переменные обладают экономическим смыслом. Поскольку, в ограничениях начальной задачи линейного программирования отображаются затраты и наличие производственных ресурсов, значит численное значение дополнительной переменной в плане задачи, вписанной в форме основной, равно объему неприменяемого соответствующего ресурса.
Заметим, таким образом, что если переменная 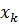 , не подчинена условию неотрицательности, то ее надо поменять двумя неотрицательными переменными
, не подчинена условию неотрицательности, то ее надо поменять двумя неотрицательными переменными 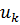 и
и 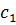 , приняв
, приняв 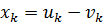 .
.
|
|
