Студопедия

Главная страница Случайная страница

Разделы сайта

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника






  • Как продвинуть сайт на первые места?
    Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.
    Ускорение продвижения
    Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.
    Начать продвижение сайта

    • Решение задачи методом ветвей и границ 1 страница. Согласно методу для каждой целочисленной переменной возможно задать верхнюю и нижнюю границу, в пределах которых содержится ее оптимальное значение


    ⇐ ПредыдущаяСтр 2 из 5Следующая ⇒




    Согласно методу для каждой целочисленной переменной возможно задать верхнюю и нижнюю границу, в пределах которых содержится ее оптимальное значение. В данном случае нижняя граница равна нулю. На практике верхний предел не вводят в виде дополнительного ограничения, а учитывают его в процессе решения не явно, то есть к исходным ограничения на практике добавляется ограничение, которое определяется самим методом.

    Решаем исходную задачу - Задачу №1 (п.1.3) до получения оптимального решения методом линейного программирования. Воспользуемся итоговой таблицей (Таблица 1.13). Эта таблица и будет исходной для нашей задачи (Таблица 2.1.6).

    Таблица 2.1.6

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8
    X5         -5     -2  
    X1 9/2       -1   -1/2    
    X2 7/4       -2   1/4 -1 1/2
    X3 5/4       -1   -1/4   1/2
    Y -16                

     

    Полученное решение не удовлетворяет требованиям целочисленности.

    Поэтому составляем относительно любой нецелочисленной переменной две новых порожденных задачи (2 и 3). Выберем переменную x1. ПримемY1 = 0.

    Новые ограничения строятся по формуле:

    1) х ≤ [х*]

    2) x ≥ [х*] + 1

    где [х*] – целая часть числа х* (нецелочисленная переменная)

    Задача №2:

    Добавляется ограничение x1≥ 5. Тогда задача примет вид:

     

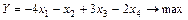
    При ограничениях:

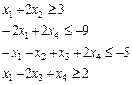
    x1≥ 5

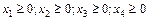    и целые.

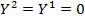
    Выразим допустимый базис в форме Таккера:

    x5=-3-(-x1-2x2+0x3+0x4)

    x6=-9-(-2x1+0x2+0x3+2x4)

    x7=-5-(-x1-x2+x3+2x4)

    x8=-2-(-x1+0x2+2x3-x4)

    x9=-5-(-x1+0x2+0x3+0x4)

    Целевая функция в форме Таккера

    Y=0-(4x1+x2-3x3+2x4)

     

    Таблица 2.1.7

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9
    X5 -3 -1 -2 0 0 1 0 0 0 0
    X6 -9 -2 0 0 2 0 1 0 0 0
    X7 -5 -1 -1 1 2 0 0 1 0 0
    X8 -2 -1 0 2 -1 0 0 0 1 0
    X9 -5 -1 0 0 0 0 0 0 0 1
    Y 0 4 1 -3 2 0 0 0 0 0

    Используем двойственный симплекс-метод. Вводим в базис x1, выводим из базиса x6

    Таблица 2.1.8

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9
    X5 3/2   -2   -1   -1/2      
    X1 9/2       -1   -1/2      
    X7 -1/2   -1       -1/2      
    X8 5/2       -2   -1/2      
    X9 -1/2       -1   -1/2      
    Y -18     -3            

    Используем двойственный симплекс-метод. Вводим в базис x2, выводим из базиса x7

    Таблица 2.1.9

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9
    X5 5/2     -2 -3   1/2 -2    
    X1 9/2       -1   -1/2      
    X2 1/2     -1 -1   1/2 -1    
    X8 5/2       -2   -1/2      
    X9 -1/2       -1   -1/2      
    Y -37/2     -2     3/2      

    Используем двойственный симплекс-метод. Вводим в базис x6, выводим из базиса x9

    Таблица 2.1.10

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9
    X5       -2 -4     -2    
    X1                   -1
    X2       -1 -2     -1    
    X8         -1         -1
    X6                   -2
    Y -20     -2            

    Используем обычный симплекс-метод. Вводим в базис x3, выводим из базиса x8

    Таблица 2.1.11

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9
    X5         -5     -2    
    X1                   -1
    X2 3/2       -5/2     -1 1/2 1/2
    X3 3/2       -1/2       1/2 -1/2
    X6                   -2
    Y -17                  

    Решение данной задачи: Y=-17; X=(5; 3/2; 3/2; 0; 5; 1; 0; 0; 0)

     

    Решение данной задачи не удовлетворяет требованиям целочисленности, поэтому необходимо простроить две порождённые задачи.

    Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
    Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM. SeoHammer делает продвижение сайта прозрачным и простым занятием. Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
    Что умеет делать SeoHammer
    — Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
    — Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
    — Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
    — SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
    SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней.
    Зарегистрироваться и Начать продвижение

    Для образования порожденных задач выберем переменную x2

    Задача №4:

    Добавляется ограничение x2≥ 2.

    Выразим допустимый базис в форме Таккера:

    x5=-3-(-x1-2x2+0x3+0x4)

    x6=-9-(-2x1+0x2+0x3+2x4)

    x7=-5-(-x1-x2+x3+2x4)

    x8=-2-(-x1+0x2+2x3-x4)

    x9=-5-(-x1+0x2+0x3+0x4)

    x10=-2-(0x1-x2+0x3+0x4)

    Целевая функция в форме Таккера

    Y=0-(4x1+x2-3x3+2x4)

    Таблица 2.1.12

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
    X5 -3 -1 -2                
    X6 -9 -2                  
    X7 -5 -1 -1                
    X8 -2 -1     -1            
    X9 -5 -1                  
    X10 -2   -1                
    Y       -3              

    Используем двойственный симплекс-метод. Вводим в базис x1, выводим из базиса x6

    Таблица 2.1.13

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
    X5 3/2   -2   -1   -1/2        
    X1 9/2       -1   -1/2        
    X7 -1/2   -1       -1/2        
    X8 5/2       -2   -1/2        
    X9 -1/2       -1   -1/2        
    X10 -2   -1                
    Y -18     -3              

    Используем двойственный симплекс-метод. Вводим в базис x2, выводим из базиса x10

    Таблица 2.1.14

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
    X5 11/2       -1   -1/2       -2
    X1 9/2       -1   -1/2        
    X7 3/2           -1/2       -1
    X8 5/2       -2   -1/2        
    X9 -1/2       -1   -1/2        
    X2                     -1
    Y -20     -3              

    Используем двойственный симплекс-метод. Вводим в базис x6, выводим из базиса x9

    Таблица 2.1.15

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
    X5                   -1 -2
    X1                   -1  
    X7                   -1 -1
    X8         -1         -1  
    X6                   -2  
    X2                     -1
    Y -22     -3              

    Используем обычный симплекс-метод. Вводим в базис x3, выводим из базиса x8

    Таблица 2.1.16

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
    X5                   -1 -2
    X1                   -1  
    X7 1/2       5/2       -1/2 -1/2 -1
    X3 3/2       -1/2       1/2 -1/2  
    X6                   -2  
    X2                     -1
    Y -35/2       1/2       3/2 5/2  

    Решение данной задачи: Y=-35/2; X=(5; 2; 3/2; 0; 6; 1; 1/2; 0; 0; 0)

     

    Решение данной задачи не удовлетворяет требованиям целочисленности, поэтому необходимо простроить две порождённые задачи.

     

    Для образования порожденных задач выберем переменную x3

    Задача №6:

    Добавляется ограничение x3≥ 2

    Выразим допустимый базис в форме Таккера

    x5=-3-(-x1-2x2+0x3+0x4)

    x6=-9-(-2x1+0x2+0x3+2x4)

    x7=-5-(-x1-x2+x3+2x4)

    x8=-2-(-x1+0x2+2x3-x4)

    x9=-5-(-x1+0x2+0x3+0x4)

    x10=-2-(0x1-x2+0x3+0x4)

    x11=-2-(0x1+0x2-x3+0x4)

    Целевая функция в форме Таккера

    Y=0-(4x1+x2-3x3+2x4)

    Таблица 2.1.17

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11
    X5 -3 -1 -2                  
    X6 -9 -2                    
    X7 -5 -1 -1                  
    X8 -2 -1     -1              
    X9 -5 -1                    
    X10 -2   -1                  
    X11 -2     -1                
    Y       -3                

    Используем двойственный симплекс-метод. Вводим в базис x1, выводим из базиса x6

    Таблица 2.1.18

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11
    X5 3/2   -2   -1   -1/2          
    X1 9/2       -1   -1/2          
    X7 -1/2   -1       -1/2          
    X8 5/2       -2   -1/2          
    X9 -1/2       -1   -1/2          
    X10 -2   -1                  
    X11 -2     -1                
    Y -18     -3                

    Используем двойственный симплекс-метод. Вводим в базис x2, выводим из базиса x10

    Таблица 2.1.19

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11
    X5 11/2       -1   -1/2       -2  
    X1 9/2       -1   -1/2          
    X7 3/2           -1/2       -1  
    X8 5/2       -2   -1/2          
    X9 -1/2       -1   -1/2          
    X2                     -1  
    X11 -2     -1                
    Y -20     -3                

    Используем двойственный симплекс-метод. Вводим в базис x3, выводим из базиса x11

    Таблица 2.1.20

    БП СЧ X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11
    X5 11/2       -1   -1/2       -2  
    X1 9/2       -1   -1/2          
    X7 -1/2           -1/2       -1  
    X8 -3/2       -2   -1/2          
    X9 -1/2       -1   -1/2          
    X2                     -1  
    X3                       -1
    Y -14                     -3

    Используем двойственный симплекс-метод. Вводим в базис x4, выводим из базиса x8


    ⇐ Предыдущая12345Следующая ⇒




    © 2023 :: MyLektsii.ru :: Мои Лекции
    Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав.
    Копирование текстов разрешено только с указанием индексируемой ссылки на источник.