Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Примеры решения задач. 1. Определить, сколько трехзначных чисел можно составить из множества цифр 7,8,9,3,2 без повторений.

1. Определить, сколько трехзначных чисел можно составить из множества цифр 7, 8, 9, 3, 2 без повторений.

Решение. Трехзначные числа можно рассматривать как размещения, так как при замене одной цифры другой или перестановке их местами получаются разные числа. Так как n=5, k=3, то различных чисел будет:

А 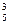=5·4·3=60.

2. К кассе за получением (или для уплаты) денег подошли одновременно 4 человека. Сколькими способами они могут выстроиться в очередь?

Решение. Очередь состоит из 4 различных лиц, поэтому в каждом способе составления очереди учитывается порядок их расположения. Таким образом, имеют место перестановки из четырёх человек, их число равно:

Р₄ = 4! = 24.

3.В цехе 18 человек, из них 10 мужчин. На конференцию отбирают 6 человек так, что было 3 мужчины и 3 женщины. Сколько различных списков можно составить?

Решение. 3-х мужчин из 10 человек можно отобрать С 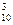различными способами, 3-х женщин из 8 можно отобрать С 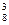различными способами. Следовательно, 3-х женщин и 3-х мужчин можно отобрать 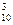С · С 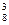– различными способами.

Найдем: С = = ,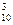

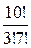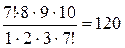С = = .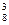

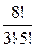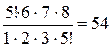Итого, число различных списков:

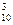С ∙ С 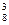= 120 · 54 = 6480.

Основные понятия теории вероятностей

Определение. Результат некоторого опыта или эксперимента, который нельзя заранее предсказать назовем случайным событием.

События обозначаются большими латинскими буквами: А, В, С, …

Примеры наиболее часто встречающихся испытаний и событий приведены в таблице.

Определение. Достоверным назовем событие, которое обязательно произойдет в результате опыта.

Например, из урны с 20 красными шарами обязательно будет вынут красный шар.

Определение. Невозможным назовем событие, которое заведомо не произойдет в результате опыта.

Например, из урны с 20 красными шарами не будет вынут зеленый шар.

Определение. События А и В называются несовместными, если появление одного из них исключает появление другого, в противном случае события называются совместными.

Рассмотрим пример. События: А – из колоды вынута крестовая карта, В – из колоды вынута бубновая карта, D – из колоды вынута дама.

События А и В – несовместные. События А и D – совместные, так как из колоды может быть вынута дама крестей, в этом случае произойдет и событие А – крестовая карта, и событие D – дама.

Определение. События А и 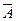называются противоположными, если событие 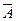происходит всякий раз, когда не происходит событие А и наоборот.

Например, событие А –выпал герб при бросании монеты и событие 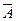– выпала цифра– противоположное.

Определение. События называются равновозможными, если нет основания считать, что одно из них произойдет скорее, чем другое.

Определение. Элементарными событиями назовем все результаты испытания, которые являются попарно несовместными и равновозможными. Те элементарные события, в которых наступает событие А, назовем благоприятствующими появлению события А.

Определение. Вероятностью события А (обозначается Р(А)) называется отношение числа m благоприятствующих исходов к общему числу n элементарных исходов опыта (классическое определение вероятности).

Итак, вероятность события А определяется формулой:

Р(А)= ,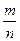

где m – число элементарных событий, благоприятствующих событию А, n – число всех элементарных исходов испытания.

Например, в урне 10 красных и 7 зеленых шаров, достаем 1 шар. Рассмотрим события: А – из урны вынут красный шар, В – из урны вынут зеленый шар. Найдём вероятности этих событий.

Решение: всего в урне 17 шаров, тогда n = 17. Благоприятствующими исходами для события А будет извлечение любого из 10 красных шаров, то есть m = 10, таким образом Р(А)= 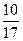; аналогично, Р(В)= .

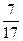Пример. На конференцию из группы студентов из 20 человек (8 девушек, 12 юношей) отбирают 5 человек. Найти вероятность следующих событий:

А – среди отобранных студентов одни юноши,

В – среди отобранных студентов одни девушки,

С – среди отобранных 2 девушки и 3 юношей.

Решение. Заметим, что общее число исходов для всех трех событий будет одинаковым n= C .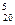

Число благоприятствующих исходов: m_А = C 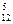, m_В = C 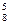, m_С = C 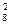∙ С .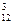

Следовательно, получаем вероятность появления события А:

Р(А)= = = =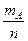

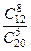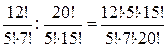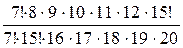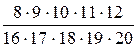= = = 0, 051.

Найдем вероятность появления события В.

Р(В)= 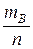= = 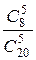= = 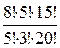=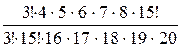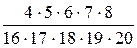0, 006

Аналогично получаем:

Р(С)= = = = =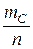

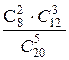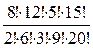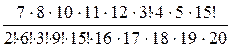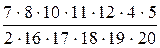= = 0, 0795.

Заметим, что вероятность достоверного события равна 1, а вероятность невозможного равна 0. Вероятность случайного события А заключена между 0 и 1. Итак, для любого события верно неравенство: 0 ≤ Р(А) ≤ 1.