Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Общие правила комбинаторики.

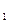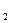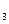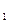Рассмотрим k множеств М , М , М , …, М , содержащих по m 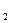, m , m 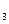, …, m элементов соответственно. Выбирается по одному элементу из каждого множества и составляется еще одно множество. Число способов, которыми можно выбрать по одному элементу из каждого множества, равно произведению 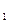m 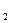∙ m ∙ m 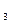∙ …∙ m . В этом и состоит основной принцип произведения комбинаторики.

В задачах теории вероятностей часто рассматриваются различные соединения (комбинации) k элементов из множества, содержащего n элементов (k≤ n). Будем рассматривать такие соединения, в которые каждый элемент данного множества может входить не более одного раза, то есть соединения без повторений. Рассмотрим три вида соединений: размещения, перестановки, сочетания.

Определение. Размещениями из n элементов по k элементов называются наборы k элементов, отличающиеся один от другого или самими элементами (составом элементов), или их порядком. Число размещений обозначается A .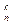

Число размещений из n элементов по k элементов находится по формуле:

А 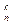=n∙ (n–1)∙ (n–2)∙ …∙ (n–(k–1)). (1)

Определение. Перестановками из данных n элементов называются наборы из n элементов, различающихся только порядком.

Перестановки – это частный случай размещений. Число всех перестановок обозначают символом Р 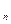. Число Р 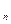найти несложно. Для этого в формулу (1) подставляем k=n.

Р 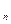=n∙ (n–1)∙ (n–2)∙ …∙ (n–(k–1))∙ …∙ 2∙ 1=n!

Определение. Произведение n первых натуральных чисел называется факториалом числа n и обозначается символом n! (читается «эн факториал»).

Р 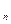=1·2·3 …∙ n=n! (2)

Приведем некоторые значения факториала:

0! =1, 5! = 1·2·3·4∙ 5=120,

1! =1, 6! = 1·2·3·4∙ 5∙ 6=720,

2! =1·2=2, 7! = 1·2·3·4∙ 5∙ 6∙ 7=5040,

3! =1·2·3=6, 8! = 1·2·3·4∙ 5∙ 6∙ 7∙ 8=40320,

4! =1·2·3·4=24, 9! = 1·2·3·4∙ 5∙ 6∙ 7∙ 8∙ 9=362880.

Определение. Сочетаниями, содержащими k элементов, выбранных из n элементов заданного множества, называются всевозможные наборы k элементов, различающиеся хотя бы одним элементом. Число сочетаний из n элементов по k элементов обозначают С 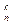или (.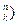

Число сочетаний из n элементов по k элементов определяется формулой:

С 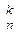=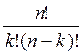