Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Переход от прямой задачи к двойственной
|
|
Общая задача линейного программирования формулируется следующим образом максимизировать (минимизировать) целевую функцию Y вида:
Y=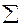 
cjxj → max
При ограничениях
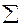aijxj(< =, =, > =)bi i=[1, m]; j=[1, n]; xj> =0
Прямая задача линейного программирования:
Y=с1*x1+…+сn*xn → max
При ограничениях
a11*x1+…a1n*xn< =b1
a21*x1+…a2n*xn< =b2
....
ak1*x1+…akn*xn< =bk
xi> =0, i=[1, n]
Двойственная задача:
S=b1*y1+…+bm*ym → min
При ограничениях
a11*y1+…am1*ym> =c1
a12*y1+…am2*ym> =c2
....
a1n*x1+…amn*ym> =cn
yi> =0, j=[1, m]
Правила образования двойственной задачи:
1. Целевая функция исходной задачи оптимизируется противоположно двойственной.
2. Матрица коэффициентов ограничений двойственной задачи получается путём транспонирования матрицы коэффициентов прямой задачи и наоборот.
3. Число переменных в двойственной задаче равно числу ограничений прямой задачи, а число ограничений двойственной задачи равно числу переменных прямой задачи.
4. Коэффициентами при неизвестных целевой функции двойственной задачи являются свободные члены системы ограничений прямой задачи, а правыми частями системы ограничений двойственной задачи являются коэффициенты целевой функции исходной задачи.
5. Если переменная xj прямой задачи может принимать только положительное значение, то j-е условие в системе ограничений двойственной задачи является неравенством вида > =. Если переменная xj может принимать любое значение, то j-е ограничение уравнение =. Аналогичное состояние имеется между ограничениями исходной задачи и переменными двойственной задачи.
|
|