Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод пространства состояния. Представление двухмассовой системы в переменных состояния
|
|
Наряду с представленной моделью в переменных «входы-выходы», в которой используются передаточные функции отдельных звеньев и построенные из них структурные схемы, в настоящее время для моделирования сложных систем используют метод «пространства состояний».
В математическом описании метода присутствуют не только входные воздействия и выходные переменные, но и внутренние промежуточные переменные, число которых равно числу дифференциальных уравнений входящих в систему, которые и называются переменными состояния. Все эти переменные образуют структуру, представленную на рис.6, где:
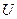- входные переменные;
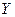- входные переменные;
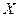- переменные состояния.
Рис.6 Структурная схема метода переменных состояния
В общем виде решения задачи для любой системы в переменных состояния сводится к решению системы 2-х уравнений:
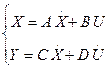
Структурная схема данной системы представлена на рис.7.
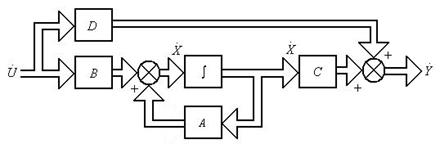
Рис.7 Структурная схема системы в переменных состояния
В данной структурной схеме введены следующие обозначения.
1. 
- вектор состояния системы.
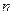- число уравнений.
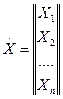
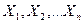- соответственно для каждого из уравнений переменная, выраженная в каждом из уравнений в качестве входных
2. 
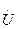- вектор входных переменных
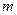- число входных переменных
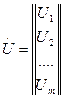
3. 
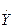-вектор выходных переменных
- число выходных переменных
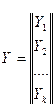
4. 
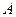- матрица промежуточных переменных или параметрическая матрица, которая представляет собой матрицу коэффициентов при переменных состояния.
Номер строки - номер уравнения. Номер столбца - номер переменной состояния.
5. 
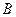- входная матрица системы представляет собой матрицу коэффициентов перед входными переменными.
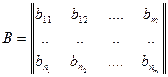
Номер строки - номер уравнения. Номер столбца - номер переменной.
6. 
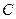- выходная матрица системы - параметрическая матрица.
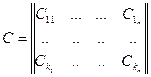
Номер строки - номер выходной переменной. Номер столбца - номер уравнения.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
7. 
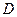- проходная матрица - матрица коэффициентов перед членами уравнений связи между входными и выходными величинами.
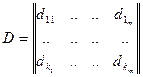
Для 2-х массовой механической системы имеем следующее решение.
, 
, 
, 
, 
.
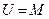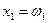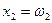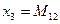Уравнения (4) - (6) относительно производных:
, 
, 
, , 
.
, 
,
, 
,
, 
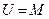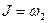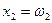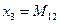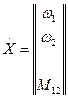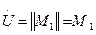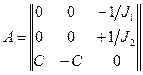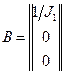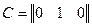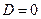
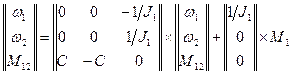
В итоге:
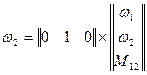(10)
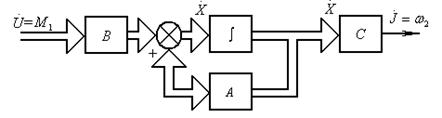
Рис.8 Структурная схема двухмассовой механической системы в переменных состояния
|
|