Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сместиться на (27, 12)

КОНЕЦ ПОВТОРИ

сместиться на (–22, -7)

КОНЕЦ

Укажите наименьшее возможное значение числа n (n > 1), для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.

Решение:

1) запишем общее изменение координат Чертёжника в результате выполнения этого алгоритма:

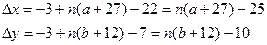
2) поскольку Чертёжник должен вернуться в исходную точку, эти величины должны быть равны нулю; следовательно, нужно найти наименьшее натуральное n > 1, при котором система уравнений

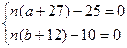
разрешима в целых числах относительно a и b

3) несложно заметить, что для этого число n должно быть одновременно делителем чисел 10 и 25

4) наименьший общий делитель чисел 10 и 25 равен 5

5) ответ – 5.

Ещё пример задания:

Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b – целые числа), перемещающую Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Если числа a, b положительные, значение соответствующей координаты увеличивается, если отрицательные – уменьшается. Например, если Чертёжник находится в точке с координатами (2, 4), то команда Сместиться на (1, –5) переместит Чертёжника в точку (3, –1).

Запись

Повтори k раз

Команда1

Команда2

Команда3

конец

означает, что последовательность команд Команда1 Команда2 Команда3 повторится k раз.

Чертёжнику был дан для исполнения следующий алгоритм:

Сместиться на (3, -3)

Повтори N раз

Сместиться на (27, 17)

Сместиться на (a, b)

конец

Сместиться на (–27, –17)

Чему должно равняться N, чтобы Чертежник смог вернуться в исходную точку, из которой он начал движение?

1) 4 2) 5 3) 6 4) 7

Решение:

6) обратим внимание, что в этой задаче значения a и b неизвестны

7) вычислим итоговое смещение Чертёжника (общее изменение каждой координаты должно быть равно 0):

(3, -3)

N раз (27+a, 17+b)

(-27, 17)

общее изменение x-координаты:

3+N(27+a)-27 = 0

общее изменение y-координаты:

-3+N(17+b)-17 = 0

8) упрощаем оба уравнения:

N(27+a) = 24

N(17+b) = 20

9) таким образом, N – общий делитель чисел 24 и 20, это может быть 2 или 4; из вариантов ответа, приведённых в задаче, подходит только 4 (ответ 1)

10) Ответ: 1.

Ещё пример задания:

Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости: