
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сместиться на (-1, -2)
|
|
Сместиться на (a, b)
КОНЕЦ ПОВТОРИ
сместиться на (–24, -12)
КОНЕЦ
Укажите наибольшее возможное значение числа n, для которого найдутся такие значения чисел a и b, что после выполнения программы Чертёжник возвратится в исходную точку.
Решение:
1) запишем общее изменение координат Чертёжника в результате выполнения этого алгоритма:

2) поскольку Чертёжник должен вернуться в исходную точку, эти величины должны быть равны нулю; следовательно, нужно найти набольшее натуральное n, при котором система уравнений
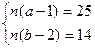
разрешима в целых числах относительно a и b
3) несложно заметить, что для этого число n должно быть одновременно делителем чисел 14 и 25
4) наибольший общий делитель чисел 14 и 25 равен 1
5) ответ – 1.
Ещё пример задания:
Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на ( a, b ), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a; y + b). Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, − 3) переместит Чертёжника в точку (6, − 1).
Цикл
ПОВТОРИ число РАЗ
последовательность команд
КОНЕЦ ПОВТОРИ
означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным). Чертёжнику был дан для исполнения следующий алгоритм (буквами n, a, b обозначены неизвестные числа, при этом n > 1):
НАЧАЛО
сместиться на (–3, –3)
ПОВТОРИ n РАЗ
|
|
